Classe System.Drawing.Drawing2D.Matrix

Este artigo fornece comentários complementares à documentação de referência para esta API.

A Matrix classe encapsula uma matriz de affine 3 por 3 que representa uma transformação geométrica.

No GDI+, você pode armazenar uma transformação de affine em um Matrix objeto. Como a terceira coluna de uma matriz que representa uma transformação affine é sempre (0, 0, 1), você especifica apenas os seis números nas duas primeiras colunas ao construir um objeto Matrix. A instrução Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) constrói a matriz mostrada na figura a seguir.

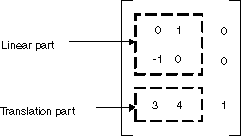
Observação

No .NET 6 e versões posteriores, o pacote System.Drawing.Common, que inclui esse tipo, só tem suporte em sistemas operacionais Windows. O uso desse tipo em aplicativos multiplataforma causa avisos de tempo de compilação e exceções em tempo de execução. Para obter mais informações, consulte System.Drawing.Common com suporte apenas no Windows.

Transformações compostas

Uma transformação composta é uma sequência de transformações, uma seguida pela outra. Considere as matrizes e transformações na seguinte lista:

Matriz	Transformação
Matriz A	Girar 90 graus
Matriz B	Dimensionar por um fator de 2 na direção x
Matriz C	Mover 3 unidades na direção y

Se você começar com o ponto (2, 1) - representado pela matriz [2 1 1] - e multiplicar por A, então B, C, o ponto (2, 1) passará pelas três transformações na ordem listada.

[2 1 1]ABC = [-2 5 1]

Em vez de armazenar as três partes da transformação composta em três matrizes separadas, você pode multiplicar A, B e C juntos para obter uma única matriz 3×3 que armazena toda a transformação composta. Suponha que ABC = D. Em seguida, um ponto multiplicado por D fornece o mesmo resultado que um ponto multiplicado por A e, em seguida, B e C.

[2 1 1]D = [-2 5 1]

A ilustração a seguir mostra as matrizes A, B, C e D.

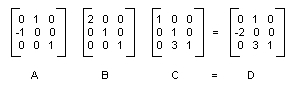
O fato de que a matriz de uma transformação composta pode ser formada multiplicando as matrizes de transformação individuais significa que qualquer sequência de transformações de afim pode ser armazenada em um único objeto Matrix.

Cuidado

A ordem de uma transformação composta é importante. Em geral, girar, dimensionar e converter não é o mesmo que dimensionar, girar e converter. Da mesma forma, a ordem da multiplicação de matriz é importante. Em geral, ABC não é o mesmo que BAC.

A classe Matrix fornece vários métodos para a criação de uma transformação composta: Multiply, Rotate, RotateAt, Scale, Sheare Translate. O exemplo a seguir cria a matriz de uma transformação composta que primeiro gira 30 graus, depois escala por um fator de 2 na direção y, e finalmente translada 5 unidades na direção x:

Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);

Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)