Visão geral da transformação

As transformações de matriz lidam com muitos dos cálculos de baixo nível dos gráficos 3D.

O pipeline de geometria recebe vértices como entrada. O mecanismo de transformação aplica as transformações de mundo, de visualização e de projeção aos vértices, recorta o resultado e passa tudo para o rasterizador.

Transformação e espaço	Descrição
Coordenadas de modelo no espaço do modelo	No início do pipeline, os vértices de um modelo são declarados em relação a um sistema de coordenadas local. Essa é uma origem local e uma orientação. Essa orientação de coordenadas geralmente é conhecida como espaço de modelo. Coordenadas individuais são chamadas de coordenadas de modelo.
Transformação do mundo em espaço mundial	O primeiro estágio do pipeline de geometria transforma os vértices de um modelo de seu sistema de coordenadas local para um sistema de coordenadas que é usado por todos os objetos em uma cena. O processo de reorientar os vértices é chamado de transformação World , que converte do espaço de modelo para uma nova orientação chamada de espaço global . Cada vértice no espaço mundial é declarado usando coordenadas mundo.
Exibir transformação em espaço de exibição (espaço da câmera)	No próximo estágio, os vértices que descrevem seu mundo 3D são orientados em relação a uma câmera. Ou seja, seu aplicativo escolhe um ponto de vista para a cena e as coordenadas de espaço do mundo são realocadas e giradas em torno da exibição da câmera, transformando o espaço do mundo em espaço de exibição (também conhecido como espaço de câmera). Este é o transformador View, que converte do espaço de mundo para o espaço de visualização.
Transformação de projeção em espaço de projeção	O próximo estágio é a transformação Projeção, que converte do espaço de exibição para o espaço de projeção. Nesta parte do pipeline, os objetos geralmente são dimensionados em relação à distância do observador, a fim de dar a ilusão de profundidade a uma cena; objetos próximos parecem maiores do que objetos distantes. Para simplificar, esta documentação refere-se ao espaço no qual os vértices existem após à transformação projetiva como espaço de projeção. Alguns livros sobre gráficos podem se referir ao espaço de projeção como espaço homogêneo pós-perspectiva. Nem todas as transformações de projeção dimensionam o tamanho dos objetos em uma cena. Uma projeção como essa às vezes é chamada de de afim ou de projeção ortogonal.
Recorte no espaço da tela	Na parte final do pipeline, todos os vértices que não estarão visíveis na tela são removidos, de modo que o rasterizador não tenha tempo para calcular as cores e o sombreamento para algo que nunca será visto. Esse processo é chamado de recorte. Após o recorte, os vértices restantes são dimensionados de acordo com os parâmetros da janela de exibição e convertidos em coordenadas de tela. Os vértices resultantes, vistos na tela quando a cena é rasterizada, existem em espaço de tela.

 

As transformações são usadas para converter a geometria do objeto de um espaço de coordenadas em outro. O Direct3D usa matrizes para executar transformações 3D. Matrizes criam transformações 3D. Você pode combinar matrizes para produzir uma única matriz que engloba várias transformações.

Você pode transformar coordenadas entre o espaço do modelo, o espaço mundial e o espaço de exibição.

• World transform – Converte do espaço modelo para o espaço mundial.
• Transformação de visualização - Converte do espaço do mundo para o espaço de visualização.
• Transformação de projeção - converte do espaço de visualização para o espaço de projeção.

Transformações de Matriz

Em aplicativos que funcionam com gráficos 3D, você pode usar transformações geométricas para fazer o seguinte:

• Expresse a localização de um objeto em relação a outro objeto.
• Girar e dimensionar objetos.
• Alterar as posições de exibição, as direções e as perspectivas.

Você pode transformar qualquer ponto (x,y,z) em outro ponto (x', y', z') usando uma matriz 4x4, conforme mostrado na equação a seguir.

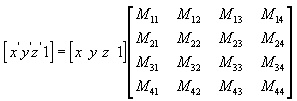
Execute as seguintes equações em (x, y, z) e a matriz para produzir o ponto (x', y', z').

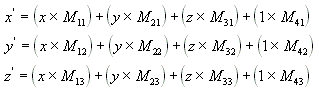
As transformações mais comuns são tradução, rotação e dimensionamento. Você pode combinar as matrizes que produzem esses efeitos em uma única matriz para calcular várias transformações ao mesmo tempo. Por exemplo, você pode criar uma única matriz para traduzir e girar uma série de pontos.

Matrizes são escritas na ordem linha-coluna. Uma matriz que dimensiona uniformemente vértices ao longo de cada eixo, conhecida como dimensionamento uniforme, é representada pela matriz a seguir usando notação matemática.

No C++, o Direct3D declara matrizes como uma matriz bidimensional usando um struct de matriz. O exemplo a seguir mostra como inicializar uma estrutura D3DMATRIX para atuar como uma matriz de dimensionamento uniforme (fator de escala "s").

D3DMATRIX scale = {
    5.0f,            0.0f,            0.0f,            0.0f,
    0.0f,            5.0f,            0.0f,            0.0f,
    0.0f,            0.0f,            5.0f,            0.0f,
    0.0f,            0.0f,            0.0f,            1.0f
};

Traduzir

A equação a seguir converte o ponto (x, y, z) para um novo ponto (x', y', z').

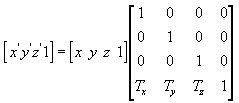
Você pode criar manualmente uma matriz de tradução no C++. O exemplo a seguir mostra o código-fonte de uma função que cria uma matriz para traduzir vértices.

D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
    D3DXMATRIX ret;

    D3DXMatrixIdentity(&ret);
    ret(3, 0) = dx;
    ret(3, 1) = dy;
    ret(3, 2) = dz;
    return ret;
}    // End of Translate

Escala de

A equação a seguir dimensiona o ponto (x, y, z) por valores arbitrários nas direções x, y e z para um novo ponto (x', y', z').

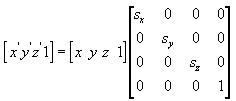
Girar

As transformações descritas aqui são para sistemas de coordenadas esquerdos e podem, portanto, ser diferentes das matrizes de transformação que você viu em outro lugar.

A equação a seguir gira o ponto (x, y, z) em torno do eixo x, produzindo um novo ponto (x', y', z').

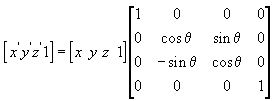
A equação a seguir gira o ponto em torno do eixo y.

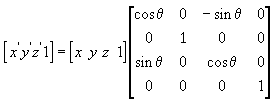
A equação a seguir gira o ponto em torno do eixo z.

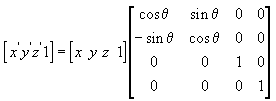
Nestas matrizes de exemplo, a letra grega theta significa o ângulo de rotação, em radianos. Os ângulos são medidos no sentido horário ao olhar ao longo do eixo de rotação em direção à origem.

O código a seguir mostra uma função para lidar com a rotação sobre o eixo X.

    // Inputs are a pointer to a matrix (pOut) and an angle in radians.
    float sin, cos;
    sincosf(angle, &sin, &cos);  // Determine sin and cos of angle

    pOut->_11 = 1.0f; pOut->_12 =  0.0f;   pOut->_13 = 0.0f; pOut->_14 = 0.0f;
    pOut->_21 = 0.0f; pOut->_22 =  cos;    pOut->_23 = sin;  pOut->_24 = 0.0f;
    pOut->_31 = 0.0f; pOut->_32 = -sin;    pOut->_33 = cos;  pOut->_34 = 0.0f;
    pOut->_41 = 0.0f; pOut->_42 =  0.0f;   pOut->_43 = 0.0f; pOut->_44 = 1.0f;

    return pOut;
}

Concatenando Matrizes

Uma vantagem de usar matrizes é que você pode combinar os efeitos de duas ou mais matrizes multiplicando-as. Isso significa que, para girar um modelo e traduzi-lo para algum local, você não precisa aplicar duas matrizes. Em vez disso, você multiplica as matrizes de rotação e tradução para produzir uma matriz composta que contenha todos os efeitos. Esse processo, chamado concatenação de matriz, pode ser escrito com a equação a seguir.

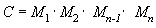
Nesta equação, C é a matriz composta que está sendo criada e M₁ por meio de Mn são as matrizes individuais. Na maioria dos casos, apenas duas ou três matrizes são concatenadas, mas não há limite.

A ordem na qual a multiplicação de matriz é executada é crucial. A fórmula anterior reflete a regra da esquerda para a direita da concatenação de matriz. Ou seja, os efeitos visíveis das matrizes que você usa para criar uma matriz composta ocorrem em ordem da esquerda para a direita. Uma matriz de mundo típica é mostrada no exemplo a seguir. Imagine que você está criando a matriz mundial para um disco voador estereotipado. Você provavelmente gostaria de girar o disco voador em torno de seu centro - o eixo y do espaço modelo - e movê-lo para algum outro local em sua cena. Para realizar esse efeito, primeiro crie uma matriz de rotação e, em seguida, multiplique-a por uma matriz de tradução, conforme mostrado na equação a seguir.

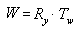
Nesta fórmula, R_y é uma matriz para rotação sobre o eixo y e T_w é uma tradução para alguma posição em coordenadas mundiais.

A ordem na qual você multiplica as matrizes é importante porque, ao contrário da multiplicação de dois valores escalares, a multiplicação de matriz não é comutativa. Multiplicar as matrizes na ordem oposta tem o efeito visual de mover o disco voador para sua posição espacial mundial e, em seguida, girá-lo ao redor da origem mundial.

Não importa o tipo de matriz que você está criando, lembre-se da regra da esquerda para a direita para garantir que você alcance os efeitos esperados.

Tópicos relacionados

transforma