Rotação

Muitos aplicativos CAD fornecem recursos que giram objetos desenhados na área do cliente. Os aplicativos que incluem recursos de rotação usam a função SetWorldTransform para definir o espaço de mundo apropriado para a transformação de espaço de página. Essa função recebe um ponteiro para uma estrutura XFORM que contém os valores apropriados. Os membros eM11, eM12, eM21 e eM22 de XFORM especificam respectivamente, o cosseno, o seno, o seno negativo e o cosseno do ângulo de rotação.

Quando ocorre rotação , os pontos que constituem um objeto são girados em relação à origem do espaço de coordenadas. A ilustração a seguir mostra um retângulo de 20 por 20 unidades girado 30 graus quando copiado do espaço de coordenadas mundiais para o espaço de coordenadas de página.

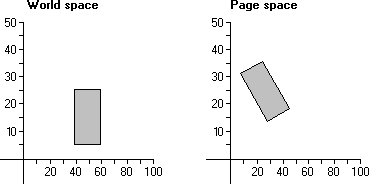
Na ilustração anterior, cada ponto no retângulo foi girado 30 graus em relação à origem do espaço de coordenadas.

O algoritmo a seguir calcula a nova coordenada x (x ') para um ponto (x,y ) que é girado pelo ângulo A em relação à origem do espaço de coordenadas.

x' = (x * cos A) - (y * sin A) 

O algoritmo a seguir calcula a coordenada y (y ) para um ponto (x,y ) que é girado pelo ângulo A em relação à origem.

y' = (x * sin A) + (y * cos A) 

As duas transformações de rotação podem ser combinadas em uma matriz de 2 por 2 da seguinte maneira.

|x' y'| == |x y| * | cos A   sin A| 
                   |-sin A   cos A| 

A matriz 2 por 2 que produziu a rotação contém os valores a seguir.

| .8660    .5000| 
|-.5000    .8660| 

Derivação de algoritmo de rotação

Os algoritmos de rotação são baseados no teorema de adição da trigonometria informando que a função trigonométrica de uma soma de dois ângulos (A1 e A2 ) pode ser expressa em termos das funções trigonométricas dos dois ângulos.

sin(A1 + A2) = (sin A1 * cos A2) + (cos A1 * sin A2) 
cos(A1 + A2) = (cos A1 * cos A2) - (sin A1 * sin A2) 

A ilustração a seguir mostra um ponto p girado no sentido anti-horário para uma nova posição p'. Além disso, ele mostra dois triângulos formados por uma linha desenhada da origem do espaço de coordenadas para cada ponto e uma linha desenhada de cada ponto pelo eixo x.

Usando trigonometria, a coordenada x do ponto p pode ser obtida multiplicando o comprimento da hipotenusa h pelo cosseno de A1.

x = h * cos A1 

A coordenada y do ponto p pode ser obtida multiplicando o comprimento do hipotenuoso h pelo seno de A1.

y = h * sin A1 

Da mesma forma, a coordenada x do ponto p' pode ser obtida multiplicando o comprimento da hipotenusa h pelo cosseno de (A1 +A2 ).

x' = h * cos (A1 + A2) 

Por fim, a coordenada y do ponto p' pode ser obtida multiplicando o comprimento da hipotenusa h pelo seno de (A1 +A2 ).

y' = h * sin (A1 + A2) 

Usando o teorema de adição, os algoritmos anteriores se tornam os seguintes:

x' = (h * cos A1 * cos A2) - (h * sin A1 * sin A2) 
y' = (h * cos A1 * sin A2) + (h * sin A1 * cos A2) 

Os algoritmos de rotação para um determinado ponto girado pelo ângulo A2 podem ser obtidos substituindo x por cada ocorrência de (h * cos A1 ) e substituindo y por cada ocorrência de (h * sin A1 ).

x' = (x * cos A2) - (y * sin A2) 
y' = (x * sin A2) + (y * cos A2)