Поделиться через

dcount() (статистическая функция)

  • Статья

Область применения: ✅Microsoft Fabric✅Azure Data Explorer✅Azure Monitor✅Microsoft Sentinel

Вычисляет оценку количества различных значений, принимаемых скалярным выражением в сводной группе.

Значения NULL игнорируются и не учитываются в вычислении.

Примечание.

Статистическая функция dcount() в основном полезна для оценки кратности огромных наборов. Он торгует точностью для производительности и может возвращать результат, который зависит от выполнения. Порядок входных данных может влиять на выходные данные.

Примечание.

Эта функция используется в сочетании с оператором сводки.

Синтаксис

dcount(expr[, точность])

Дополнительные сведения о соглашениях синтаксиса.

Параметры

Имя (название) Type Обязательно Описание
expr string ✔️ Входные данные, значения которых должны быть подсчитываются.
точность int Значение, определяющее запрошенную точность оценки. Значение по умолчанию — 1. См . сведения о точности оценки поддерживаемых значений.

Возвраты

Возвращает оценку количества различных значений expr в группе.

Пример

В этом примере показано, сколько типов событий шторма произошло в каждом состоянии.

StormEvents
| summarize DifferentEvents=dcount(EventType) by State
| order by DifferentEvents

Показанная таблица результатов содержит только первые 10 строк.

Штат Разные события
TEXAS 27
CALIFORNIA 26
ПЕНСИЛЬВАНИЯ 25
ДЖОРДЖИЯ 24
ИЛЛИНОЙС 23
МЭРИЛЕНД 23
СЕВЕРНАЯ КАРОЛИНА 23
МИЧИГАН 22
FLORIDA 22
ОРЕГОН 21
КАНЗАС 21
... ...

Точность оценки

Эта функция использует вариант алгоритма HyperLogLog (HLL), который выполняет стохастиическую оценку кратности набора. Алгоритм предоставляет "рычаг управления", который можно использовать для выравнивания точности и времени выполнения под размер памяти:

Правильность Ошибка (%) Число записей
0 1,6 212
1 0,8 214
2 0,4 216
3 0,28 217
4 0,2 218

Примечание.

Столбец "число записей" — это количество 1-байтных счетчиков в реализации HLL.

Алгоритм включает в себя некоторые положения для выполнения идеального подсчета (нулевой ошибки), если кратность набора достаточно мала:

  • если уровень точности равен 1, возвращаются значения 1000;
  • если уровень точности равен 2, возвращаются значения 8000.

Границы погрешности — вероятностная, а не теоретическая граница. Значение является стандартным отклонением распределения погрешностей (сигма). 99,7 % оценок будут иметь относительную погрешность в 3 сигмы.

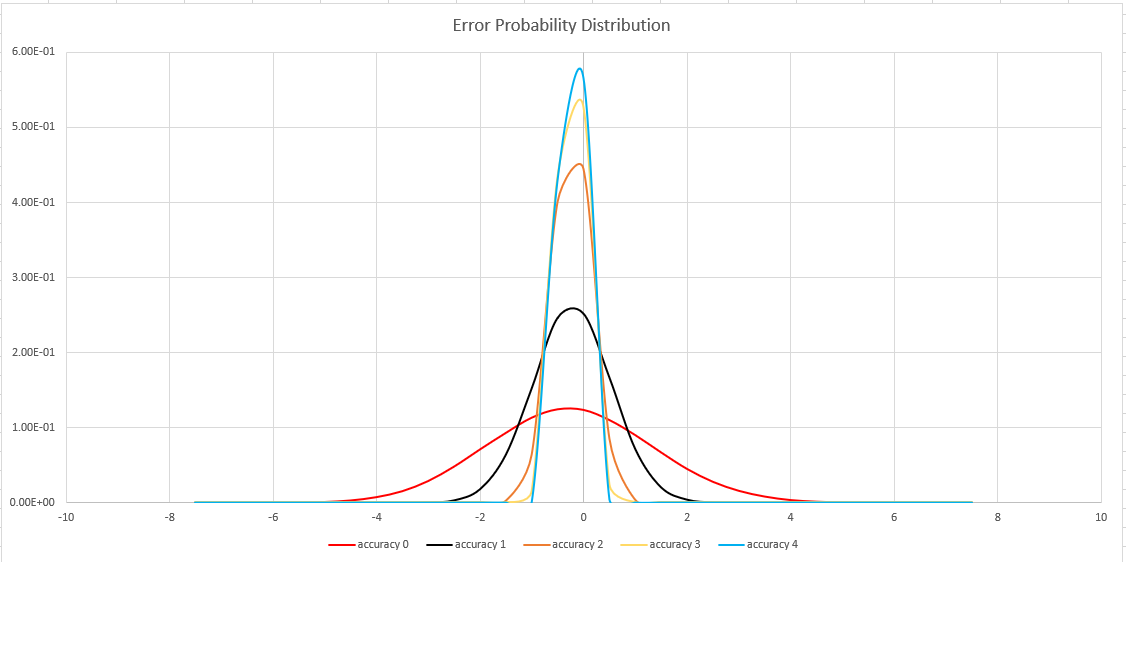
На следующем изображении показана функция распределения вероятности относительной погрешности оценки (в процентах) для всех поддерживаемых параметров точности:

График, показывающий распределение ошибок hll.