Заметка
Доступ к этой странице требует авторизации. Вы можете попробовать войти в систему или изменить каталог.
Доступ к этой странице требует авторизации. Вы можете попробовать сменить директорию.
Использование SkiaSharp для отрисовки любой строки, которую можно определить с помощью уравнений параметрики
В разделе "Кривые и пути SkiaSharp" этого руководства вы увидите различные методы, определяющие SKPath для отображения определенных типов кривых. Однако иногда необходимо нарисовать тип кривой, который не поддерживается SKPathнапрямую. В таком случае можно использовать полилайн (коллекцию подключенных линий) для рисования любой кривой, которую можно математически определить. Если вы делаете линии достаточно маленькими и достаточно многочисленными, результат будет выглядеть как кривая. Эта спираль на самом деле составляет 3600 маленьких линий:

Как правило, лучше всего определить кривую с точки зрения пары параметрических уравнений. Это уравнения для координат X и Y, которые зависят от третьей переменной, иногда вызываемой t для времени. Например, следующие параметрические уравнения определяют круг с радиусом 1 по центру в точке (0, 0) для t от 0 до 1:
x = cos(2πt)
y = sin(2πt)
Если требуется радиус размером более 1, можно просто умножить значения синуса и косинуса на этот радиус, а если нужно переместить центр в другое расположение, добавьте следующие значения:
x = xCenter + radius·cos(2πt)
y = yCenter + radius·sin(2πt)
Для многоточия с осями параллельно с горизонтальной и вертикальной, используются два радия:
x = xCenter + xRadius·cos(2πt)
y = yCenter + yRadius·sin(2πt)
Затем можно поместить эквивалентный код SkiaSharp в цикл, который вычисляет различные точки и добавляет их в путь. Следующий код SkiaSharp создает SKPath объект для многоточия, заполняющего поверхность отображения. Цикл циклов проходит через 360 градусов напрямую. Центр составляет половину ширины и высоты поверхности дисплея, поэтому два радии:
SKPath path = new SKPath();
for (float angle = 0; angle < 360; angle += 1)
{
double radians = Math.PI * angle / 180;
float x = info.Width / 2 + (info.Width / 2) * (float)Math.Cos(radians);
float y = info.Height / 2 + (info.Height / 2) * (float)Math.Sin(radians);
if (angle == 0)
{
path.MoveTo(x, y);
}
else
{
path.LineTo(x, y);
}
}
path.Close();
Это приводит к многоточию, определенной 360 маленькими линиями. Когда он отрисовывается, он отображается гладко.
Конечно, вам не нужно создавать многоточие с помощью полилайна, так как SKPath включает в себя AddOval метод, который это делает для вас. Но может потребоваться нарисовать визуальный объект, который не предоставляется SKPath.
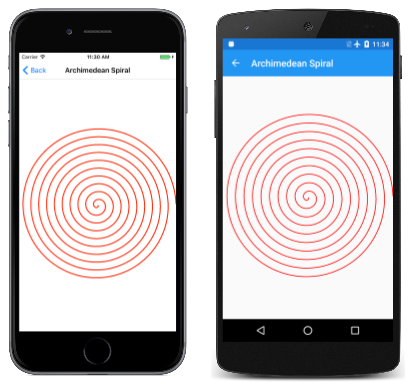
На странице Archimedean Spiral есть код, аналогичный коду многоточия, но с важным различием. Он циклит вокруг 360 градусов круга 10 раз, постоянно настраивая радиус:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
float radius = Math.Min(center.X, center.Y);
using (SKPath path = new SKPath())
{
for (float angle = 0; angle < 3600; angle += 1)
{
float scaledRadius = radius * angle / 3600;
double radians = Math.PI * angle / 180;
float x = center.X + scaledRadius * (float)Math.Cos(radians);
float y = center.Y + scaledRadius * (float)Math.Sin(radians);
SKPoint point = new SKPoint(x, y);
if (angle == 0)
{
path.MoveTo(point);
}
else
{
path.LineTo(point);
}
}
SKPaint paint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 5
};
canvas.DrawPath(path, paint);
}
}
Результат также называется арифметической спирали , так как смещение между каждым циклом является константой:
Обратите внимание, что он SKPath создается в блоке using . Это SKPath потребляет больше памяти, чем SKPath объекты в предыдущих программах, что предполагает, что using блок более подходящий для удаления неуправляемых ресурсов.