Неаффинные преобразования
Создание эффектов перспективы и касания с помощью третьего столбца матрицы преобразования
Преобразование, масштабирование, поворот и перемыка все классифицируются как аффинные преобразования. Аффинные преобразования сохраняют параллельные линии. Если две строки параллельны перед преобразованием, они остаются параллельными после преобразования. Прямоугольники всегда преобразуются в параллелограммы.
Тем не менее, SkiaSharp также способен неаффинные преобразования, которые имеют возможность преобразовать прямоугольник в любой выпуклый квадрилятор:

Выпуклая четырехсторонняя фигура с углами интерьера всегда меньше 180 градусов и сторон, которые не пересекают друг друга.
Неаффинные преобразования приводят к результату, если третья строка матрицы преобразования имеет значения, отличные от 0, 0 и 1. SKMatrix Полное умножение:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z' |
│ TransX TransY Persp2 │
Результирующий формулы преобразования:
x' = ScaleX·x + SkewX·y + TransX
y' = SkewY·x + ScaleY·y + TransY
z' = Persp0·x + Persp1·y + Persp2
Основное правило использования матрицы 3-к-3 для двухмерных преобразований заключается в том, что все остается на плоскости, где Z равно 1. Если Persp0 значение не Persp1 равно 0 и Persp2 равно 1, преобразование переместило координаты Z из этой плоскости.
Чтобы восстановить это в двухмерное преобразование, координаты должны быть перемещены обратно в эту плоскость. Требуется еще один шаг. Значения x', y'и z должны быть разделены на z':
x" = x' / z'
y" = y' / z'
z" = z' / z' = 1
Они известны как однородные координаты , и они были разработаны математиком Августом Фердинандом Мёбиусом, гораздо более известным за его топологическую странность, Мёбиус полосы.
Если z' равно 0, деление приводит к бесконечным координатам. На самом деле, одна из мотиваций Möbius для разработки однородных координат была способность представлять бесконечные значения с конечными числами.
Однако при отображении графики необходимо избежать отрисовки чего-либо с координатами, которые преобразуются в бесконечные значения. Эти координаты не будут отображаться. Все в окрестностях этих координат будет очень большим и, вероятно, не визуально последовательным.
В этом уравнении не требуется, чтобы значение z стало нулевым:
z' = Persp0·x + Persp1·y + Persp2
Следовательно, эти значения имеют некоторые практические ограничения:
Ячейка Persp2 может быть нулевой или не нулевой. Если Persp2 значение равно нулю, то z ' равно нулю для точки (0, 0), и это обычно не желательно, потому что эта точка очень распространена в двухмерной графике. Если Persp2 не равно нулю, то при исправлении 1 отсутствует потеря общего характера Persp2 . Например, если определить, что Persp2 должно быть 5, можно просто разделить все ячейки в матрице на 5, что равно Persp2 1, и результат будет одинаковым.
По этим причинам Persp2 часто фиксируется значение 1, которое является одинаковым значением в матрице удостоверений.
Как правило, Persp0 и Persp1 это небольшие числа. Например, предположим, что вы начинаете с матрицы удостоверений, но установите значение Persp0 0,01:
| 1 0 0.01 | | 0 1 0 | | 0 0 1 |
Формулы преобразования:
x ' = x / (0.01·x + 1)
y' = y / (0,01·x + 1)
Теперь используйте это преобразование для отрисовки прямоугольник с 100 пикселей, расположенный в источнике. Вот как преобразуются четыре угла:
(0, 0) → (0, 0)
(0, 100) → (0, 100)
(100, 0) → (50, 0)
(100, 100) → (50, 50)
Если значение x равно 100, то знаменатель z равен 2, поэтому координаты x и y эффективно сокращены. Правая сторона поля становится короче левой стороны:

Persp Часть этих имен ячеек ссылается на "перспективу", потому что форешортенинг предполагает, что поле теперь наклоняется с правой стороны дальше от средства просмотра.
Страница "Проверка перспективы" позволяет экспериментировать со значениями Persp0 и Pers1 получить представление о том, как они работают. Разумные значения этих матрицных ячеек настолько малы, что Slider в универсальная платформа Windows не может правильно обрабатывать их. Чтобы решить проблему UWP, необходимо инициализировать два Slider элемента в Файле TestPerspective.xaml в диапазоне от –1 до 1:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.TestPerspectivePage"
Title="Test Perpsective">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Minimum" Value="-1" />
<Setter Property="Maximum" Value="1" />
<Setter Property="Margin" Value="20, 0" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="persp0Slider"
Grid.Row="0"
ValueChanged="OnPersp0SliderValueChanged" />
<Label x:Name="persp0Label"
Text="Persp0 = 0.0000"
Grid.Row="1" />
<Slider x:Name="persp1Slider"
Grid.Row="2"
ValueChanged="OnPersp1SliderValueChanged" />
<Label x:Name="persp1Label"
Text="Persp1 = 0.0000"
Grid.Row="3" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="4"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Обработчики событий для ползунка в TestPerspectivePage файле программной части разделяют значения на 100, чтобы они были диапазоном от –0,01 до 0,01. Кроме того, конструктор загружается в растровом рисунке:
public partial class TestPerspectivePage : ContentPage
{
SKBitmap bitmap;
public TestPerspectivePage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnPersp0SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp0Label.Text = String.Format("Persp0 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
void OnPersp1SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp1Label.Text = String.Format("Persp1 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
...
}
Обработчик PaintSurface вычисляет SKMatrix значение с именем perspectiveMatrix на основе значений этих двух ползунков, разделенных на 100. Это в сочетании с двумя преобразованиями перевода, которые помещают центр этого преобразования в центр растрового изображения:
public partial class TestPerspectivePage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Calculate perspective matrix
SKMatrix perspectiveMatrix = SKMatrix.MakeIdentity();
perspectiveMatrix.Persp0 = (float)persp0Slider.Value / 100;
perspectiveMatrix.Persp1 = (float)persp1Slider.Value / 100;
// Center of screen
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
SKMatrix.PostConcat(ref matrix, perspectiveMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(xCenter, yCenter));
// Coordinates to center bitmap on canvas
float x = xCenter - bitmap.Width / 2;
float y = yCenter - bitmap.Height / 2;
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
}
Ниже приведены некоторые примеры изображений:
Поэкспериментируя с ползунками, вы обнаружите, что значения, превышающие 0,0066 или ниже –0,00666, приводят к тому, что изображение внезапно становится переломным и несогласованным. Преобразуемая растровая карта составляет 300 пикселей. Он преобразуется относительно центра, поэтому координаты растрового изображения варьируются от –150 до 150. Помните, что значение z':
z' = Persp0·x + Persp1·y + 1
Если Persp0 или Persp1 больше 0,0066 или ниже –0,0066, то всегда имеется некоторая координата растрового изображения, которая приводит к значению z от нуля. Это приводит к делении на нулю, и отрисовка становится беспорядок. При использовании неаффинных преобразований необходимо избежать отрисовки с координатами, которые вызывают деление на ноль.
Как правило, вы не будете устанавливать Persp0 и Persp1 в изоляции. Также часто необходимо задать другие ячейки в матрице для достижения определенных типов неаффинных преобразований.
Одним из таких неаффинных преобразований является преобразование касания. Этот тип неаффинного преобразования сохраняет общие размеры прямоугольника, но коснитесь одной стороны:
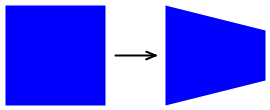
Класс TaperTransform выполняет обобщенное вычисление неаффинного преобразования на основе следующих параметров:
- прямоугольный размер преобразуемого изображения,
- перечисление, указывающее сторону прямоугольника, который касается,
- другое перечисление, указывающее, как он касается, и
- степень сцепивания.
Вот этот код:
enum TaperSide { Left, Top, Right, Bottom }
enum TaperCorner { LeftOrTop, RightOrBottom, Both }
static class TaperTransform
{
public static SKMatrix Make(SKSize size, TaperSide taperSide, TaperCorner taperCorner, float taperFraction)
{
SKMatrix matrix = SKMatrix.MakeIdentity();
switch (taperSide)
{
case TaperSide.Left:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp0 = (taperFraction - 1) / size.Width;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Top:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp1 = (taperFraction - 1) / size.Height;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Right:
matrix.ScaleX = 1 / taperFraction;
matrix.Persp0 = (1 - taperFraction) / (size.Width * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
break;
}
break;
case TaperSide.Bottom:
matrix.ScaleY = 1 / taperFraction;
matrix.Persp1 = (1 - taperFraction) / (size.Height * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
break;
}
break;
}
return matrix;
}
}
Этот класс используется на странице преобразования taper. Xaml-файл создает экземпляры двух Picker элементов для выбора значений перечисления, а также Slider для выбора дроби касания. Обработчик PaintSurface объединяет преобразование касания с двумя преобразованиями перевода, чтобы сделать преобразование относительно левого верхнего угла растрового изображения:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
TaperSide taperSide = (TaperSide)taperSidePicker.SelectedItem;
TaperCorner taperCorner = (TaperCorner)taperCornerPicker.SelectedItem;
float taperFraction = (float)taperFractionSlider.Value;
SKMatrix taperMatrix =
TaperTransform.Make(new SKSize(bitmap.Width, bitmap.Height),
taperSide, taperCorner, taperFraction);
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(taperMatrix);
matrixDisplay.Paint(canvas, taperMatrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Center bitmap on canvas
float x = (info.Width - bitmap.Width) / 2;
float y = (info.Height - bitmap.Height) / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-x, -y);
SKMatrix.PostConcat(ref matrix, taperMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(x, y));
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
Далее приводятся некоторые примеры.
Другим типом обобщенных неаффинных преобразований является трехмерная смена, которая показана в следующей статье, трехмерные повороты.
Неаффинное преобразование может преобразовывать прямоугольник в любой выпуклый четырехлатеральный. Это демонстрируется на странице "Показать неаффинированные матрицы ". Это очень похоже на страницу Show Affine Matrix из статьи "Преобразования матрицы", за исключением того, что он имеет четвертый объект для управления четвертым TouchPoint углом растрового изображения:
Если вы не пытаетесь сделать внутренний угол одного из углов растрового изображения больше 180 градусов, или сделать две стороны пересекаются друг с другом, программа успешно вычисляет преобразование с помощью этого метода из ShowNonAffineMatrixPage класса:
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL, SKPoint ptLR)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
// Non-Affine transform
SKMatrix inverseA;
A.TryInvert(out inverseA);
SKPoint abPoint = inverseA.MapPoint(ptLR);
float a = abPoint.X;
float b = abPoint.Y;
float scaleX = a / (a + b - 1);
float scaleY = b / (a + b - 1);
SKMatrix N = new SKMatrix
{
ScaleX = scaleX,
ScaleY = scaleY,
Persp0 = scaleX - 1,
Persp1 = scaleY - 1,
Persp2 = 1
};
// Multiply S * N * A
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.PostConcat(ref result, S);
SKMatrix.PostConcat(ref result, N);
SKMatrix.PostConcat(ref result, A);
return result;
}
Чтобы упростить вычисление, этот метод получает общее преобразование в виде продукта трех отдельных преобразований, которые символизируются здесь со стрелками, показывающими, как эти преобразования изменяют четыре угла растрового изображения:
(0, 0) → (0, 0) → (0, 0) → (x0, y0) (в верхнем левом углу)
(0, H) → (0, 1) → (0, 1) → (x1, y1) (нижний слева)
(W, 0) → (1, 0) → (1, 0) → (x2, y2) (в правом верхнем углу)
(W, H) → (1, 1) → (a, b) → (x3, y3) (в правом нижнем углу)
Окончательные координаты справа — четыре точки, связанные с четырьмя точками касания. Это окончательные координаты углов растрового изображения.
W и H представляют ширину и высоту растрового изображения. Первое преобразование S просто масштабирует растровое изображение до квадрата 1 пикселя. Второе преобразование — это неаффинное преобразование N, а третье — аффинное преобразование A. Это аффинное преобразование основано на трех точках, поэтому это так же, как и предыдущий аффинный ComputeMatrix метод и не включает четвертую строку с точкой (a, b).
Вычисляются a и b значения, чтобы третье преобразование было аффинным. Код получает обратное преобразование аффина, а затем использует его для сопоставления нижнего правого угла. Это точка (a, b).
Другое использование неаффинных преобразований заключается в имитации трехмерной графики. В следующей статье трехмерные повороты показано, как повернуть двухмерный рисунок в трехмерном пространстве.


