Что такое суперпозиция в квантовых вычислениях?
В классическом мире реальные объекты, такие как кот и коробка, могут находиться только в одном состоянии одновременно. Но в квантовом мире частицы могут существовать в суперпозиции всех их возможных состояний.
К сожалению, нет квантовых компьютеров, использующих кошки для выполнения вычислений. Вместо этого реальные квантовые компьютеры используют кубиты, сокращённо от квантовые биты. Точно так же, как бит является базовой единицей информации в классических вычислениях, кубит является базовой единицей информации в квантовых вычислениях. И точно так же, как биты могут принимать одно из двух возможных значений, 0 и 1, кубит также имеет значение 0 или 1 при измерении.
Существует множество физических представлений кубитов. Например, поляризация фотона или спина электрона может использоваться как кубиты, так как фотоны имеют два разных состояния поляризации и электроны имеют два различных состояния спина при измерении. Мы можем представить одно из этих состояний как 0 и другое состояние как 1, и кубит всегда будет давать 0 или 1, когда мы измеряем его.
Но как мы представляем суперпозицию в кубите? И какова вероятность того, что мы находим кубита в определенном состоянии, когда мы принимаем измерение?
Представление на сфере Блоха суперпозиции для отдельных кубитов
Кубит — это квантовая частица, которая находится в одном из двух возможных состояний при измерении кубита. Независимо от физического характера кубита, мы обозначаем два состояния как 0 и 1. Кубит может находиться в состоянии 0, в состоянии 1 или в бесконечном количестве суперпозиций как 0, так и 1. Как представлять эти суперпозиции в квантовых вычислениях?
Полезное геометрическое представление состояния суперпозиции одного кубита является сферой Blockh.
Представьте, что вы рисуете круг с радиусом единицы (длина радиуса равна 1). Затем нарисуйте вертикальную и горизонтальную оси, чтобы две оси пересекались в центре круга. Теперь определим состояние 0, где вертикальная ось соответствует верхней части круга и 1 состоянию, где вертикальная ось соответствует нижней части круга. На этом круге состояния 0 и 1 находятся на расстоянии $180^\circ$, или $\pi$ радиан, друг от друга.
Как это представление относится к состоянию кубита? Мы можем представить состояние кубита в виде стрелки (или вектора) длины единицы, которая направлена от центра круга к его границе. Когда вектор указывает вертикально вверх, кубит находится в состоянии «0», а когда вектор указывает вертикально вниз, кубит находится в состоянии «1». В этом представлении классический бит будет вектором, который всегда указывает прямо вверх или прямо вниз, но никогда не в другом направлении.
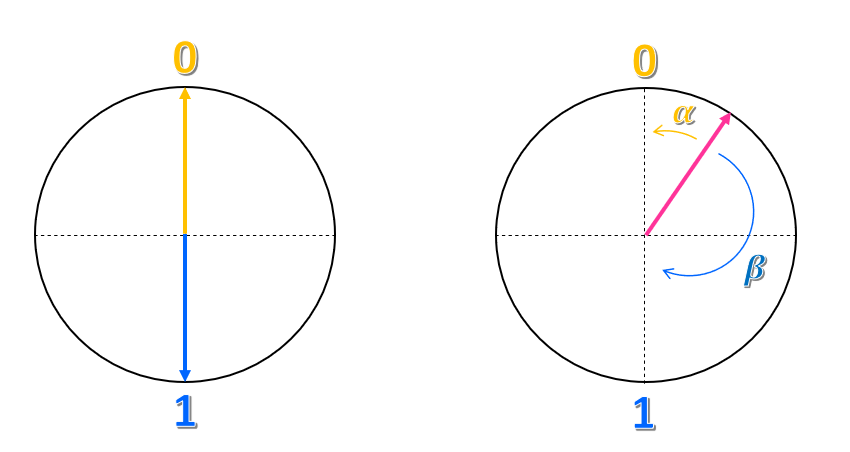
Вектор кубита может указывать в любом направлении на окружности. Каждое расположение на окружности, кроме направлений строго вверх или вниз, представляет состояние суперпозиции. Например, мы называем угол, который вектор делает с 0 состоянием $\alpha$, и угол, который вектор делает с 1 состоянием $\beta$. Затем мы представляем состояние суперпозиции кубита как $\alpha 0 + \beta 1$.
Аналогично примеру кота и коробки, состояние суперпозиции кубита — это сумма отдельных состояний, 0 и 1, взвешенная числами $\alpha$ и $\beta$. Однако в системе cat-and-box весы являются реальными числами, но в системе кубитов весы $\alpha$ и $\beta$ являются сложными числами.
Так как амплитуды $\alpha$ и $\beta$ являются сложными числами, нам нужен другой круг на схеме, которая находится в плоскости перпендикулярно первому кругу, чтобы действительно представлять любое состояние суперпозиции кубита. Эти два круга существуют в трех измерениях для производства сферы Блока.
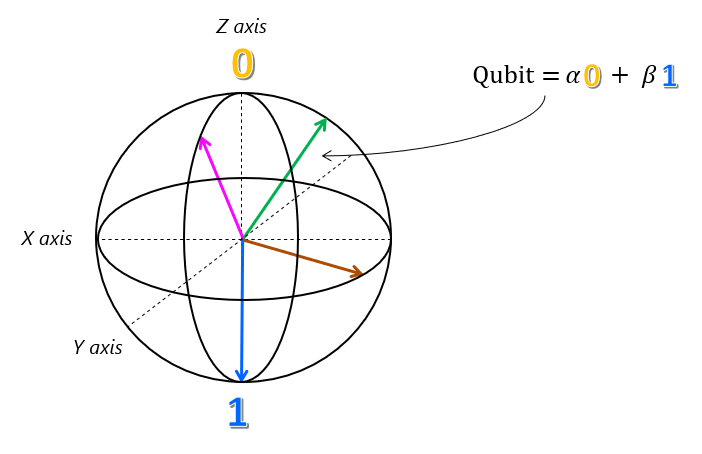
Эта область Блока является точным геометрическим представлением каждого возможного состояния суперпозиции для одного кубита. Состояние кубита представлено расположением на поверхности сферы, на которую указывает вектор. Хоть сфера Блоха и полезна, к сожалению, она не может быть расширена на системы с несколькими кубитами.
Совет
Сфера Блоха является мощным инструментом, так как операции, выполняемые на кубите во время квантовых вычислений, представлены как вращения вокруг одной из главных осей сферы Блоха. Это геометрическое представление помогает построить интуицию о том, как работают операции в квантовых вычислениях, но сложно использовать эту интуицию для проектирования и описания алгоритмов. Q# помогает предоставить язык для описания таких поворотов.
Какова вероятность поиска кубита в определенном состоянии?
В системе cat-and-box из предыдущего модуля веса для каждого состояния являются реальными числами, которые напрямую соответствуют вероятности того, что система находится в каждом состоянии. В системе кубитов числа $\alpha$ и $\beta$ находятся в общих сложных числах, которые не дают вероятности поиска кубита в 0 и 1 состояниях. Вместо этого эти числа называются амплитудами вероятности (или просто амплитудами).
Фактические вероятности вычисляются из квадратов величины амплитуд вероятности. Вероятность того, что измерение находит кубит в состоянии 0, составляет $|\alpha|^2$, и вероятность того, что измерение находит кубит в 1 состоянии : $|\beta|^2$. В общем случае, $\alpha + \beta$ не складывается до 100%, но $|\alpha|^2 + |\beta|^2$ всегда равно 100%. Ограничение , которое $|\alpha|^2 + |\beta|^2 = 1$ называется условием нормализации, и каждое допустимое квантовое состояние должно соответствовать этому условию.