Двоичная классификация
Замечание
Дополнительные сведения см. на вкладке "Текст и изображения ".
Классификация, например регрессия, является защищенным методом машинного обучения; и поэтому следует тому же итеративному процессу обучения, проверки и оценки моделей. Вместо вычисления числовых значений, таких как модель регрессии, алгоритмы, используемые для обучения моделей классификации, вычисляют значения вероятности для назначения классов и метрики оценки, используемые для оценки производительности модели, сравнивают прогнозируемые классы с фактическими классами.
Алгоритмы двоичной классификации используются для обучения модели, которая прогнозирует одну из двух возможных меток для одного класса. По сути, прогнозирование истина или ложь. В большинстве реальных сценариев наблюдения за данными, используемые для обучения и проверки модели, состоят из нескольких значений функции (x) и значения y , равное 1 или 0.
Пример — двоичная классификация
Чтобы понять, как работает двоичная классификация, рассмотрим упрощенный пример, использующий одну функцию (x) для прогнозирования того, является ли метка y 1 или 0. В этом примере мы будем использовать уровень глюкозы крови пациента для прогнозирования того, имеет ли пациент диабет. Ниже приведены данные, с помощью которых мы обучим модель:

|

|
|---|---|
| Глюкоза крови (x) | Диабетик? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
Обучение модели двоичной классификации
Чтобы обучить модель, мы будем использовать алгоритм для соответствия обучающих данных функции, которая вычисляет вероятность того, что метка класса имеет значение true (иными словами, что у пациента диабет). Вероятность измеряется как значение от 0,0 до 1,0, поэтому общая вероятность для всех возможных классов составляет 1,0. Например, если вероятность диабета у пациента составляет 0,7, то есть соответствующая вероятность 0,3, что пациент не диабетик.
Существует множество алгоритмов, которые можно использовать для двоичной классификации, например логистической регрессии, которая наследует функцию sigmoid (S-shaped) со значениями от 0,0 до 1.0, как показано ниже:
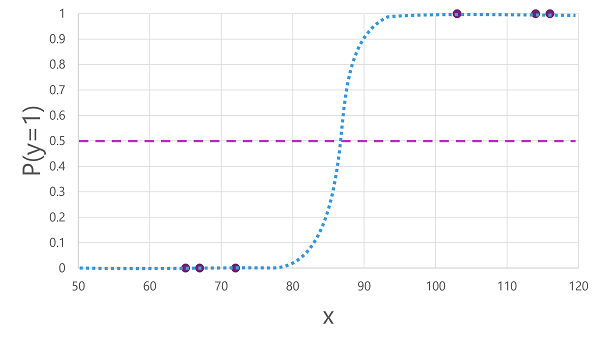
Замечание
Несмотря на свое название, в машинном обучении логистическая регрессия используется для классификации, а не регрессии. Важной точкой является логистическая природа производимой функции, которая описывает кривую S-фигуры между нижним и верхним значением (0.0 и 1.0 при использовании для двоичной классификации).
Функция, созданная алгоритмом, описывает вероятность истинности y (y=1) для заданного значения x. Математически вы можете выразить функцию следующим образом:
f(x) = P(y=1 | x)
Для трех из шести наблюдений в обучающих данных мы знаем, что y определенно верно, поэтому вероятность для этих наблюдений, что y=1 равно 1,0 и для других трех, мы знаем, что y определенно ложно, поэтому вероятность того, что y=1 равно 0,0. Кривая С-фигуры описывает распределение вероятностей таким образом, чтобы диаграмма значения x на линии идентифицировала соответствующую вероятность y 1.
Схема также включает горизонтальную линию, указывающую пороговое значение , с помощью которого модель, основанная на этой функции, будет прогнозировать значение true (1) или false (0). Порог находится в середине y (P(y) = 0,5. Для любых значений в этой точке или выше модель будет прогнозировать true (1); в то время как для любых значений ниже этой точки он будет прогнозировать false (0). Например, для пациента с уровнем глюкозы крови 90 функция приведет к значению вероятности 0,9. Поскольку 0,9 выше порогового значения 0,5, модель будет прогнозировать true (1) - другими словами, у пациента предполагается диабет.
Оценка модели двоичной классификации
Как и при регрессии, при обучении модели двоичной классификации вы удерживаете случайный подмножество данных, с помощью которых необходимо проверить обученную модель. Предположим, что мы оставили следующие данные для валидации нашего классификатора диабета:
| Глюкоза крови (x) | Диабетик? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
Применение логистической функции, полученной ранее к значениям x , приводит к следующему графику.
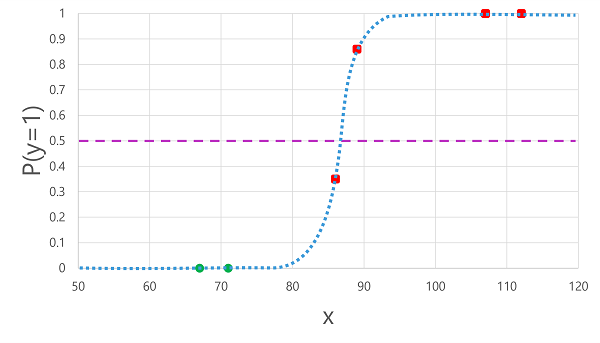
На основе того, выше или ниже порогового значения вычисленная функцией вероятность, модель определяет прогнозируемую метку 1 или 0 для каждого наблюдения. Затем можно сравнить прогнозируемые метки классов (ŷ) с фактическими метками классов (y), как показано здесь:
| Глюкоза крови (x) | Подтверждённый диагноз диабета (y) | Прогнозируемый диагноз сахарного диабета (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
Метрики оценки двоичной классификации
Первый шаг в вычислении метрик оценки для модели двоичной классификации обычно заключается в создании матрицы количества правильных и неправильных прогнозов для каждой возможной метки класса:
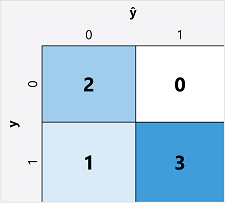
Эта визуализация называется матрицей путаницы, и она показывает итоговые итоги прогнозирования, где:
- ŷ=0 и y=0: истинные отрицания (TN)
- ŷ=1 и y=0: ложные положительные (FP)
- ŷ=0 и y=1: ложные отрицательные (FN)
- ŷ=1 и y=1: истинные положительные (TP)
Схема матрицы путаницы такова, что правильные (true) прогнозы расположены по диагонали сверху слева вниз направо. Часто цветовая интенсивность используется для указания количества прогнозов в каждой ячейке, поэтому быстрый взгляд на модель с хорошей точностью прогнозирования должен показать выраженный диагональный тренд.
Точность
Простейшая метрика, которую можно вычислить из матрицы путаницы , — точность — доля прогнозов, которые модель получила правильно. Точность вычисляется следующим образом:
(TN+TP) ÷ (TN+FN+FP+TP)
В нашем примере диабета вычисляется:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0.83
Поэтому для наших данных проверки модель классификации диабета произвела правильные прогнозы 83% времени.
Точность может первоначально показаться хорошей метрикой для оценки модели, но рассмотрим это. Предположим, что 11% населения имеет диабет. Вы можете создать модель, которая всегда прогнозирует 0, и она достигнет точности 89%, даже если она не делает реальных попыток различать пациентов, оценивая их особенности. Нам действительно нужно более глубокое понимание того, как модель работает при прогнозировании 1 для положительных случаев и 0 для отрицательных случаев.
отзыв товара
Отзыв — это метрика, которая измеряет долю положительных случаев, которые модель определила правильно. Другими словами, по сравнению с числом пациентов , у которых диабет, сколько модели прогнозировало диабет?
Формула отзыва:
TP ÷ (TP+FN)
Для нашего примера диабета:
3 ÷ (3+1)
= 3 ÷ 4
= 0.75
Так что наша модель правильно определила 75% пациентов, больных диабетом, как страдающих диабетом.
Точность
Точность является аналогичной метрикой для отзыва, но измеряет пропорцию прогнозируемых положительных случаев, когда истинная метка фактически положительна. Другими словами, какая доля пациентов предсказанных моделью на самом деле имеет диабет?
Формула точности:
TP ÷ (TP+FP)
Для нашего примера диабета:
3 ÷ (3+0)
= 3 ÷ 3
= 1.0
Таким образом, 100% пациентов, прогнозируемых нашей моделью как имеющих диабет, действительно имеют диабет.
Оценка F1
Оценка F1 — это общая метрика, которая объединяет полноту и точность. Формула для оценки F1:
(2 x точность x отзыв) ÷ (точность и отзыв)
Для нашего примера диабета:
(2 x 1.0 x 0.75) ÷ (1.0 + 0.75)
= 1.5 ÷ 1.75
= 0,86
Область под кривой (AUC)
Другое имя для отзыва является истинной положительной скоростью (TPR), и есть эквивалентная метрика, называемая ложноположительный коэффициент (FPR), который вычисляется как FP÷(FP+TN). Мы уже знаем, что TPR для нашей модели при использовании порогового значения 0,5 равно 0,75, и мы можем использовать формулу для FPR для вычисления значения 0÷2 = 0.
Конечно, если бы мы изменили пороговое значение, выше которого модель прогнозирует true (1), это повлияет на число положительных и отрицательных прогнозов; и, следовательно, измените метрики TPR и FPR. Эти метрики часто используются для оценки модели путем построения кривой полученных характеристик оператора (ROC), которая сравнивает TPR и FPR для каждого возможного порогового значения от 0,0 до 1.0:
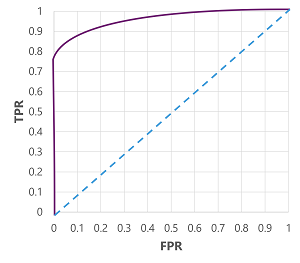
Кривая ROC для идеальной модели будет идти прямо вверх по оси TPR слева, а затем через ось FPR в верхней части. Так как область графика для кривой измеряет 1x1, область под этой идеальной кривой будет 1,0 (то есть модель правильной 100% времени). В отличие от этого, диагональная линия от нижнего левого к правому верхнему краю представляет результаты, которые были бы достигнуты при случайном угадывании двоичной метки, давая значение площади под кривой, равное 0,5. Другими словами, учитывая две возможные метки классов, можно было бы ожидать правильно угадать 50% времени.
В случае нашей модели диабета создается приведённая выше кривая, а площадь под кривой (AUC) составляет 0,875. Поскольку AUC выше 0,5, мы можем сделать вывод, что модель лучше предсказывает, имеет ли пациент диабет, чем при случайных догадках.