Что такое классификация?
Двоичная классификация — это классификация с двумя категориями. Например, пациентов можно разделить на диабетиков и не диабетиков.
Прогнозирование класса выполняется путем определения вероятности для каждого возможного класса в виде значения от 0 (невозможно) до 1 (вероятно). Общая вероятность для всех классов всегда составляет 1, так как пациент определенно диабетический или не диабетический. Таким образом, если прогнозируемая вероятность диабетического пациента составляет 0,3, то есть соответствующая вероятность 0,7, что пациент не диабетик.
Пороговое значение, часто 0,5, используется для определения прогнозируемого класса. Если положительный класс (в данном случае диабетик) имеет прогнозируемую вероятность больше порога, то прогнозируется классификация диабетика.
Обучение и оценка модели классификации
Классификация — это пример защищенного метода машинного обучения, который означает, что он использует данные, включающие известные значения признаков и известные значения меток. В этом примере значения признаков являются диагностическими измерениями для пациентов, а значения меток — классификация в категории не диабетики или диабетики. Алгоритм классификации используется для подгонки подмножества данных к функции, которая может вычислять вероятность каждой метки класса на основе значений признаков. Оставшиеся данные используются для оценки модели путем сравнения прогнозов, которые она создает из признаков для известных меток классов.
Простой пример
Давайте рассмотрим пример, который поможет объяснить ключевые принципы. Предположим, у нас есть следующие данные пациента, которые состоят из одного признака (уровень глюкозы крови) и метки класса 0 для не диабетика, 1 для диабета.
| Глюкоза в крови | Диабетик |
|---|---|
| 82 | 0 |
| 92 | 0 |
| 112 | 1 |
| 102 | 0 |
| 115 | 1 |
| 107 | 1 |
| 87 | 0 |
| 120 | 1 |
| 83 | 0 |
| 119 | 1 |
| 104 | 1 |
| 105 | 0 |
| 86 | 0 |
| 109 | 1 |
Мы используем первые восемь наблюдений для обучения модели классификации, и мы начнем с построения функции глюкозы крови (x) и прогнозируемой диабетической метки (y).
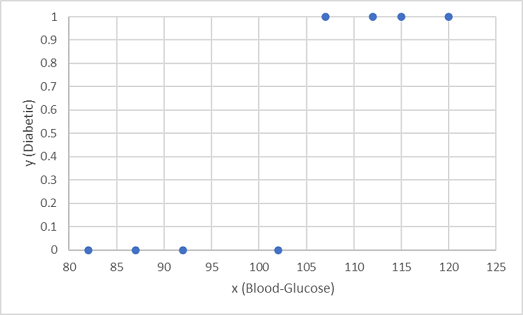
Нам нужна функция, которая вычисляет значение вероятности для y на основе x (иными словами, нам нужна функция f(x) = y). На диаграмме видно, что пациенты с низким уровнем глюкозы в крови не диабетики, а пациенты с высоким уровнем глюкозы в крови — диабетики. Кажется, чем выше уровень глюкозы в крови, тем выше вероятность того, что у пациента диабет, а точка перегиба находится где-то между 100 и 110. Необходимо подобрать функцию, которая вычисляет значение между 0 и 1 для y по этим значениям.
Одна из таких функций — это логистическая функция, которая формирует сигмоидальную (S-фигурную) кривую.
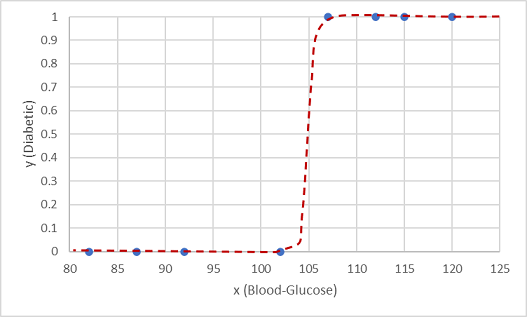
Теперь можно использовать функцию для вычисления вероятности того, что y является положительным (пациент — диабетик) с любого значения x путем нахождения точки на линии функции для x. Можно установить пороговое значение 0,5 в качестве точки отсечения для предсказания метки класса.
Давайте протестируем это с двумя значениями данных, которые мы удержали.
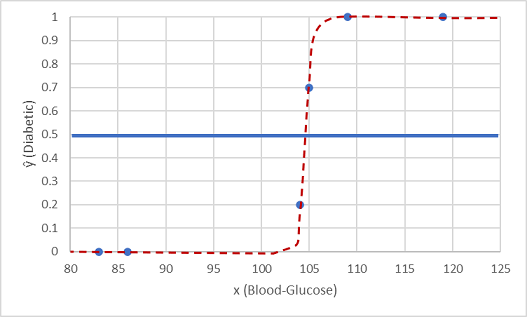
Точки, показанные ниже пороговой линии, дают прогнозируемый класс 0 (не диабетический) и точки над линией прогнозируются как 1 (диабетик).
Теперь можно сравнить прогнозы меток (ŷ или "y-hat"), основанные на логистической функции, инкапсулированной в модели, с фактическими метками классов (y).
| x | и | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |