Оценка моделей классификации
Точность обучения модели классификации гораздо менее важна по сравнению с тем, насколько хорошо модель будет работать при наличии новых данных, которые ей ранее не встречались. В конце концов, мы обучаем модели, чтобы их можно было использовать для новых данных, которые мы встречаем в реальном мире. Таким образом, после обучения модели классификации мы рассмотрим, как она выполняется в наборе новых невидимых данных.
В предыдущих разделах мы создали модель, которая дает прогноз, есть ли у пациента диабет или нет, основываясь на уровне глюкозы в крови. Теперь, когда применяется к некоторым данным, которые не были частью обучающего набора, мы получаем следующие прогнозы.
| x | г | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |
Помните, что x — это уровень глюкозы в крови, y означает, действительно ли пациент диабетик, а ŷ — это прогноз модели относительно того, является ли пациент диабетиком или нет.
Просто вычисление количества правильных прогнозов иногда вводит в заблуждение или слишком упрощенно для нас, чтобы понять виды ошибок, которые он сделает в реальном мире. Чтобы получить более подробные сведения, результаты можно оформить в табличном виде в форме структуры, именуемой матрицей неточностей, следующим образом:
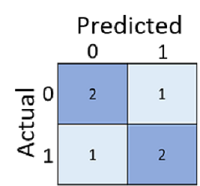
В матрице неточностей показано общее количество вариантов.
- Модель предсказала 0, а фактическая метка — 0 (истинные отрицательные, верхний левый)
- Модель предсказала 1, а фактическая метка — 1 (истинные положительные, нижний правый)
- Модель прогнозировала 0, а фактическая метка — 1 (ложные отрицательные, нижний слева)
- Модель прогнозировала 1, а фактическая метка — 0 (ложные срабатывания, верхний правый)
Ячейки в матрице путаницы часто затеняются таким образом, чтобы более высокие значения имели более глубокий оттенок. Это упрощает просмотр строгой диагонали сверху вниз слева направо благодаря выделению ячеек, в которых прогнозируемое значение совпадает с фактическими значениями.
С помощью этих основных значений можно вычислить диапазон других метрик, которые позволят оценить производительность модели. Например:
- Достоверность: (TP + TN) / (TP + TN + FP + FN) — сколько прогнозов оказались верными из общего числа?
- Полнота: TP / (TP + FN) — для всех случаев, которые являются положительными, сколько было определено моделью?
- Точность: TP / (TP + FP) — из всех случаев, когда модель спрогнозировала положительный результат, сколько фактических результатов являются положительными?