Преобразования (Direct3D 9)
Компонент Direct3D, перемещающий геометрию через фиксированный конвейер функциональной геометрии, называется модулем преобразования. Он находит модель и смотрящего в реальном мире, проецирует вершины для отображения на экране и обрезает вершины в окне просмотра. Модуль преобразования также выполняет вычисления освещения, чтобы определить рассеянные и зеркальные компоненты в каждой вершине.
Геометрический конвейер принимает вершины в качестве входных данных. Модуль преобразований применяет к вершинам мировое, видовое и проекционное преобразования, кадрирует результат и передает все в средство программной прорисовки.
В начале конвейера вершины модели объявлены относительно локальной системы координат. Локальная система координат — это локальное начало координат и ориентация. Такую ориентацию координат часто называют пространством модели, а отдельные координаты называются координатами модели.
Первый этап геометрического конвейера преобразует вершины модели из их локальной системы координат в систему координат, используемую всеми объектами в сцене. Процесс переориентации вершин называется преобразованием мира. Эту новую ориентацию обычно называют мировым пространством, и каждая вершина в мировом пространстве объявляется с помощью мировых координат.
На следующем этапе вершины, которые описывают ваш трехмерный мир, ориентируются по отношению к камере. То есть приложение выбирает точку зрения для сцены, а координаты мирового пространства перемещаются и поворачиваются вокруг обзора камеры, превращая мир в пространство камеры. Это преобразование представления.
Следующим этапом является преобразование проекции. В этой части конвейера объекты обычно масштабируются по отношению к их расстоянию от зрителя, чтобы придать сцене иллюзию глубины; Объекты close становятся больше удаленных объектов и т. д. С целью упрощения в этой документации пространство, в котором существуют вершины после проекционного преобразования, называется проекционным пространством. В некоторых книгах по графике проекционное пространство может называться постперспективным однородным пространством. Не все проекционные преобразования обеспечивают масштабирование размера объектов в сцене. Такая проекция иногда называется аффинной или ортогональной проекцией.
На последнем этапе конвейера все вершины, которые не будут видны на экране, удаляются, чтобы средство программной прорисовки не тратило время на вычисление цветов и затенения для того, что никто не увидит. Этот процесс называется кадрированием. После кадрирования оставшиеся вершины масштабируются в соответствии с параметрами окна просмотра и преобразуются в экранные координаты. Итоговые вершины, отображаемые на экране после растеризации стены, существуют в экранном пространстве.
Преобразования используются для преобразования геометрии объектов из одного пространства координат в другое. В Direct3D для 3D-преобразований используются матрицы. В этом разделе объясняется, как матрицы создают трехмерные преобразования, описаны некоторые распространенные способы использования преобразований, а также описано, как объединить матрицы для создания одной матрицы, охватывающей несколько преобразований.
- Преобразование мира (Direct3D 9) — преобразование из пространства модели в пространство мира
- Преобразование представления (Direct3D 9) — преобразование из мирового пространства в пространство просмотра
- Преобразование проекции (Direct3D 9) — преобразование из пространства представления в пространство проекции
Преобразования матрицы
В приложениях, работающих с 3D-графикой, с помощью геометрических преобразований можно:
- выражать местоположение одного объекта относительного другого объекта;
- поворачивать объекты и задавать их размер;
- менять позиции наблюдателя, направления и перспективы.
Любую точку (X,Y,Z) можно преобразовать в другую точку (X', Y', Z') с помощью матрицы 4x4, как показано в следующем уравнении.
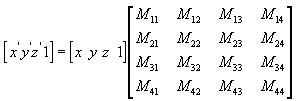
Примените следующие уравнения к (X, Y, Z) и матрице для получения точки (X', Y', Z').
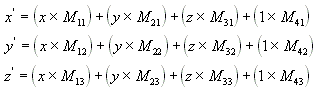
Наиболее распространенные преобразования — это параллельный перенос, поворот и масштабирование. Можно объединить матрицы, которые обеспечивают эти эффекты, в одну матрицу и вычислять сразу несколько преобразований. Например, можно построить единую матрицу для параллельного переноса и поворота серии точек.
Матрицы записываются в порядке строка-столбец. Матрица, которая равномерно масштабирует вершины вдоль каждой оси — так называемое пропорциональное масштабирование — в математической записи будет представлена следующей матрицей.

В C++ Direct3D объявляет матрицы как двумерный массив, используя структуру D3DMATRIX . В следующем примере показано, как инициализировать структуру D3DMATRIX в качестве однородной матрицы масштабирования.
// In this example, s is a variable of type float.
D3DMATRIX scale = {
s, 0.0f, 0.0f, 0.0f,
0.0f, s, 0.0f, 0.0f,
0.0f, 0.0f, s, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f
};
Перевод
Следующее уравнение параллельно переносит точку (X, Y, Z) в новую точку (X', Y', Z').
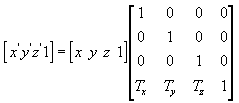
Матрицу параллельного переноса можно вручную создать в C++. В следующем примере показан исходный код для функции, которая создает матрицу для параллельного переноса вершин.
D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
D3DXMATRIX ret;
D3DXMatrixIdentity(&ret);
ret(3, 0) = dx;
ret(3, 1) = dy;
ret(3, 2) = dz;
return ret;
} // End of Translate
Для удобства библиотека служебных программ D3DX предоставляет функцию D3DXMatrixTranslation .
Масштабирование
Следующее уравнение масштабирует точку (X, Y, Z) на произвольные значения в направлениях (X, Y, Z) для получения новой точки (X', Y', Z').

Rotate
Описанные здесь преобразования предназначены для левовинтовых систем координат и, следовательно, могут отличаться от матриц преобразования, которые встречались вам где-либо еще.
Следующее уравнение поворачивает точку (X, Y, Z) вокруг оси X для получения новой точки (X', Y', Z').
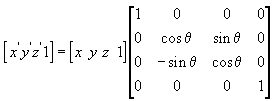
Следующее уравнение поворачивает точку вокруг оси Y.
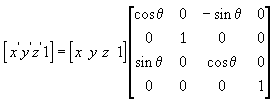
Следующее уравнение поворачивает точку вокруг оси Z.
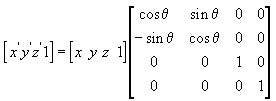
В этих примерах матриц греческой буквой тета обозначен угол поворота в радианах. Углы измеряются по часовой стрелке, если смотреть вдоль оси поворота в направлении начала координат.
В приложении C++ используйте функции D3DXMatrixRotationX, D3DXMatrixRotationY и D3DXMatrixRotationZ , предоставляемые библиотекой служебной программы D3DX, для создания матриц поворота. Ниже приведен код для функции D3DXMatrixRotationX .
D3DXMATRIX* WINAPI D3DXMatrixRotationX
( D3DXMATRIX *pOut, float angle )
{
#if DBG
if(!pOut)
return NULL;
#endif
float sin, cos;
sincosf(angle, &sin, &cos); // Determine sin and cos of angle
pOut->_11 = 1.0f; pOut->_12 = 0.0f; pOut->_13 = 0.0f; pOut->_14 = 0.0f;
pOut->_21 = 0.0f; pOut->_22 = cos; pOut->_23 = sin; pOut->_24 = 0.0f;
pOut->_31 = 0.0f; pOut->_32 = -sin; pOut->_33 = cos; pOut->_34 = 0.0f;
pOut->_41 = 0.0f; pOut->_42 = 0.0f; pOut->_43 = 0.0f; pOut->_44 = 1.0f;
return pOut;
}
Конкатенация матриц
Одним из преимуществ использования матриц является то, что эффекты двух или нескольких матриц можно объединить путем перемножения этих матриц. Это означает, что для поворота модели и последующего ее параллельного переноса в какое-либо место не нужно применять две матрицы. Вместо этого необходимо перемножить матрицы поворота и параллельного переноса для получения составной матрицы, содержащей все их эффекты. Этот процесс называется конкатенацией матриц и может описываться следующим уравнением.
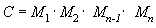
В этом уравнении C — создаваемая составная матрица, а M₁ – Mₙ — отдельные матрицы. В большинстве случаев объединяют только две или три матрицы, однако на самом деле их количество не ограничено.
Используйте функцию D3DXMatrixMultiply для выполнения матричного умножения.
Порядок, в котором выполняется перемножение матриц, имеет решающее значение. Приведенная выше формула отражает правило конкатенации матриц "слева направо". Это значит, что визуальные эффекты матриц, используемых для создания составной матрицы, имеют место в порядке слева направо. В следующем примере показана типичная мировая матрица. Предположим, вы создаете мировую матрицу для классической летающей тарелки. Наверное, имеет смысл вращать летающую тарелку вокруг ее центра — оси Y модельного пространства — и параллельно переносить ее в какое-либо другое место в сцене. Для достижения этого эффекта необходимо сначала создать матрицу поворота, а затем умножить ее на матрицу параллельного переноса, как показано в следующем уравнении.
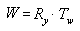
В этой формуле Ry — это матрица для поворота вокруг оси Y, а Tw — это параллельный перенос в некоторую точку в мировых координатах.
Порядок, в котором перемножаются матрицы, имеет значение, потому что, в отличие от умножения двух скалярных значений, умножение матриц не является коммутативным. Перемножение матриц в обратном порядке будет производить визуальный эффект параллельного переноса летающей тарелки в ее положение в мировом пространстве, а затем ее поворота вокруг мирового начала координат.
Вне зависимости от того, матрицу какого типа вы создаете, помните о правиле "слева направо", чтобы результаты всегда соответствовали ожидаемым.
Связанные темы