Приложение. Преобразования матрицы

В этом разделе представлен математический обзор преобразований матриц для 2-D графики. Однако для использования преобразований в Direct2D не нужно знать матричную математику. Ознакомьтесь с этой статьей, если вы заинтересованы в математике; в противном случае вы можете пропустить этот раздел.

• Введение в матрицы
  • операций матрицы
• Аффинные преобразования
  • преобразование преобразования
  • преобразование масштабирования
  • поворот вокруг источника
  • поворот вокруг произвольной точки
  • Преобразование с отклонением
• представления преобразований в Direct2D
• следующее

Общие сведения о матрицах

Матрица представляет собой прямоугольный массив реальных чисел. порядок матрицы — это количество строк и столбцов. Например, если матрица содержит 3 строки и 2 столбца, порядок равен 3 × 2. Матрицы обычно отображаются с элементами матрицы, заключенными в квадратные скобки:

Нотация: матрица обозначается прописной буквой. Элементы назначаются строчными буквами. Подстроки указывают номер строки и столбца элемента. Например,ij является элементом в строке i'th и j'th столбце матрицы A.

На следующей схеме показана матрица × j с отдельными элементами в каждой ячейке матрицы.

Операции матрицы

В этом разделе описываются основные операции, определенные в матрицах.

добавление. Сумма A + B двух матриц получается путем добавления соответствующих элементов A и B:

A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]

скалярное умножение. Эта операция умножает матрицу на реальное число. Учитывая реальное число k, скалярный продукт kA получается путем умножения каждого элемента A на k.

kA = k\[ a*ij* \] = \[ k × a*ij* \]

умножение матрицы. Учитывая два матрицы A и B с порядком (m × n) и (n × p), продукт C = A × B является матрицей с порядком (m × p), определенным следующим образом:

или, эквивалентно:

c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*

То есть для вычисления каждого элемента cijвыполните следующие действия:

1. Возьмите строку A и столбец J'th B.
2. Умножьте каждую пару элементов в строке и столбце: первая запись строки на первую запись столбца, вторую запись строки на второй столбец и т. д.
3. Суммирует результат.

Ниже приведен пример умножения матрицы (2 × 2) на матрицу (2 × 3).

Умножение матрицы не является коммутативным. То есть A × B ≠ B × A. Кроме того, из определения следует, что не каждая пара матриц может быть умножена. Число столбцов в левой матрице должно совпадать с количеством строк в правой матрице. В противном случае оператор × не определен.

Определение матрицы. Матрица удостоверений, назначенная I, представляет собой квадратную матрицу, определенную следующим образом:

I*ij* = 1, если *i* = *j*, или 0 в противном случае.

Другими словами, матрица удостоверений содержит 1 для каждого элемента, где номер строки равен номеру столбца и нулю для всех остальных элементов. Например, ниже приведена матрица 3 × 3 удостоверения.

матрица удостоверений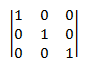

Следующие равные значения хранятся для любой матрицы M.

M x I = M I x M = M

Аффинные преобразования

Преобразование аффинного преобразования является математической операцией, которая сопоставляет одно координатное пространство с другим. Другими словами, он сопоставляет один набор точек с другим набором точек. Аффинные преобразования имеют некоторые функции, которые делают их полезными в компьютерной графике.

• Аффинные преобразования сохраняют коллинарности. Если три или более точек падают на линию, они по-прежнему образуют линию после преобразования. Прямые линии остаются прямыми.
• Композиция двух аффинных преобразований — это аффинное преобразование.

Аффинные преобразования для 2-D пространства имеют следующую форму.

При применении определения умножения матрицы, заданного ранее, можно показать, что произведение двух аффинных преобразований является еще одним аффинным преобразованием. Чтобы преобразовать 2D-точку с помощью аффинного преобразования, точка представлена в виде матрицы 1 × 3.

P = \| x y 1 \|

Первые два элемента содержат координаты x и y точки. 1 помещается в третий элемент, чтобы сделать математические вычисления правильной. Чтобы применить преобразование, умножьте две матрицы следующим образом.

P' = P × M

Это расширяется до следующего.

где

x ' = ax + cy + e y' = bx + dy + f

Чтобы получить преобразованную точку, примите первые два элемента матрицы P'.

p = (x', y') = (ax + cy + e, bx + dy + f)

Заметка

Матрица 1 × n называется в ектором строк. Direct2D и Direct3D используют векторы строк для представления точек в 2D или трехмерном пространстве. Вы можете получить эквивалентный результат с помощью вектора столбца (n × 1) и транспонирования матрицы преобразования. Большинство графических текстов используют форму вектора столбцов. В этом разделе представлена форма вектора строк для согласованности с Direct2D и Direct3D.

 

В следующих нескольких разделах наследуются основные преобразования.

Преобразование перевода

Матрица преобразования перевода имеет следующую форму.

преобразование перевода

Подключение точки P к этой формуле дает следующее:

P' = (*x* + *dx*, *y* + *dy*)

который соответствует точке (x, y), переведенной dx в оси X и dy в оси Y.

Преобразование масштабирования

Матрица преобразования масштабирования имеет следующую форму.

Подключение точки P к этой формуле дает следующее:

P' = (*x* * * dx*, *y* * * dy*)

который соответствует точке (x,y), масштабируемой dx и dy.

Поворот вокруг источника

Матрица для поворота точки вокруг источника имеет следующую форму.

Преобразованная точка:

P' = (*x*cos CTRL – ysin CTRL, *x*sin CTRL + *y*cosFX)

Доказательство. Чтобы показать, что P представляет поворот, рассмотрим следующую схему.

Данный:

P = (x,y)

Исходная точка для преобразования.

Φ

Угол, сформированный линией (0,0) на P.

Θ

Угол, по которому поворачивается (x,y) о источнике.

P ' = (x',y')

Преобразованная точка.

R

Длина линии (0,0) до P. Кроме того, радиус поворота.

Заметка

На этой схеме используется стандартная система координат, используемая в геометрии, где положительные точки оси y указывают вверх. Direct2D использует систему координат Windows, где положительная ось y указывает вниз.

 

Угол между осью x и линией (0,0) на P — ТС + 4. Удержание следующих удостоверений:

x = R cos CTRL y = R sin CTRL x' = R cos(Ø + Y) y' = R sin(Ø+ Ø)

Теперь решение для x' и y с точки зрения IT. По формулам сложения тригонометрии:

x' = R(cosØcos CTRL – sin CTRLSinT) = RcosTcos CTRL – RsinØsinØ y' = R(sin CTRLsCOs CTRL + cosTinT) = RsinTcos CTRL + Rcos CTRLSin RCOSSin RCOS

Подстановка, мы получаем:

x' = xcos CTRL — ysin CTRL y' = xsin CTRL + ycos CTRL

значение, соответствующее преобразованной точке P, показанной ранее.

Поворот вокруг произвольной точки

Для поворота вокруг точки (x,y), отличной от источника, используется следующая матрица.

преобразование поворота

Вы можете наследовать эту матрицу, принимая точку (x,y), чтобы быть источником.

Пусть (x1, y1) — это точка, которая приводит к повороту точки (x0, y0) вокруг точки (x,y). Мы можем наследить x1 следующим образом.

x1 = (x0 – x)cosC – (y0 – y)sin CTRL + x1 = x0cosC – y0sin CTRL + \[ (1 – cos CTRL) + ysin CTRL \]

Теперь подключите это уравнение обратно в матрицу преобразования, используя формулу x1 = ax0 + cy0 + e из более ранних версий. Используйте ту же процедуру для получения y1.

Преобразование с отклонением

Преобразование с отклонением определяется четырьмя параметрами:

• FX: сумма, которую нужно скосить вдоль оси x, измеряемой как угол от оси Y.
• Ø: сумма, которую нужно скосить вдоль оси Y, измеряемой как угол от оси x.
• (px, py): координаты x и y точки, о которой выполняется отклонение.

Преобразование отклонений использует следующую матрицу.

преобразование

Преобразованная точка:

P' = (*x* + *y*tan CTRL – *py*tanØ, *y* + *x*tanØ) — *py*tanØ

или эквивалентно:

P' = (*x* + (*y* – *py*)tanØ, *y* + (*x* – *px*)tanØ)

Чтобы узнать, как работает это преобразование, рассмотрите каждый компонент по отдельности. Параметр FX перемещает каждую точку в направлении x по сумме, равной танХ. На следующей схеме показана связь между 4 и осью x.

Ниже приведено то же отклонение, примененное к прямоугольнику:

Параметр Ø имеет тот же эффект, но вдоль оси y:

На следующей схеме показана ось y, примененная к прямоугольнику.

Наконец, параметры px и py сместить центральную точку по осям x и y.

Представление преобразований в Direct2D

Все преобразования Direct2D являются аффинными преобразованиями. Direct2D не поддерживает неаффинные преобразования. Преобразования представлены структурой D2D1_MATRIX_3X2_F. Эта структура определяет матрицу 3 × 2. Так как третий столбец аффинного преобразования всегда совпадает ([0, 0, 1]), и так как Direct2D не поддерживает преобразования, отличные от аффинных преобразований, не требуется указывать всю матрицу 3 × 3. Во внутреннем режиме Direct2D использует 3 × 3 матрицы для вычисления преобразований.

Члены D2D1_MATRIX_3X2_F называются в соответствии с их позицией индекса: элемент _11 является элементом (1,1), элементом _12 является элемент (1,2) и т. д. Хотя можно инициализировать элементы структуры напрямую, рекомендуется использовать класс D2D1::Matrix3x2F. Этот класс наследует D2D1_MATRIX_3X2_F и предоставляет вспомогательные методы для создания любого из основных преобразований аффина. Класс также определяет оператор *() для создания двух или более преобразований, как описано в применении преобразований в Direct2D.

Следующий

Модуль 4. Входные данные пользователя