Kuantum bilişiminde süper konum nedir?
Klasik dünyada, kedi ve kutu gibi gerçek nesneler aynı anda yalnızca bir durumda olabilir. Ancak kuantum dünyasında parçacıklar tüm olası durumlarının süper pozisyonunda bulunabilir.
Ne yazık ki hesaplamalar yapmak için kedi kullanan kuantum bilgisayar yok. Bunun yerine, gerçek kuantum bilgisayarlar kuantum bitleri için kısa olan kubitleri kullanır. Klasik bilgi işlemdeki temel bilgi biriminin bit olması gibi kubit de kuantum bilişimindeki temel bilgi birimidir. Bitlerin iki olası değerden birini (0 ve 1) nasıl alabildiği gibi, kubit de ölçteğe göre 0 veya 1 değerine sahiptir.
Kubitlerin birçok fiziksel gösterimi vardır. Örneğin, fotonların polarizasyonu veya elektron döndürmesi kubit olarak kullanılabilir çünkü fotonlar iki ayrı polarizasyon durumundadır ve elektronlar bunları ölçtğmızda iki ayrı döndürme durumu vardır. Bu durumlardan birini 0, diğerini 1 olarak temsil edebiliriz ve kubit ölçüldiğinde her zaman 0 veya 1 verir.
Peki bir qubit'teki süperpozisyonu nasıl temsil ederiz? Ölçüm yaptığımızda kubitin belirli bir durumda olma olasılığı nedir?
Tek kubitler için süperpozisyonun Bloch küre gösterimi
Kubit, ölçüm yapıldığında iki olası durumdan birinde bulunan bir kuantum parçacığıdır. Kubitin fiziksel yapısından bağımsız olarak iki durumu 0 ve 1 olarak etiketleyeceğiz. Kubit 0 durumunda, 1 durumunda veya hem 0 hem de 1 durumunun sonsuz sayıda süper pozisyonunda olabilir. Kuantum bilişiminde bu süper pozisyonları nasıl temsil ederiz?
Tek bir kubitin süper pozisyon durumunun yararlı geometrik gösterimi Bloch küresidir.
Birim yarıçapı (yarıçap uzunluğu 1'e eşit) olan bir daire çizersiniz. Ardından, iki eksenin dairenin ortasında kesişmesi için dikey ve yatay bir eksen çizin. Şimdi, 0 durumunu dikey eksenin dairenin üst kısmıyla buluştuğu nokta, 1 durumunu ise dikey eksenin dairenin alt kısmıyla buluştuğu nokta olarak tanımlayalım. Bu dairede, 0 ve 1 durumları birbirine $180^\circ$ veya $\pi$ radyan mesafededir.
Bu gösterimin kubitin durumuyla ilişkisi nedir? Kubitin durumunu dairenin ortasından dairenin kenarına doğru çizilmiş birim uzunluğunda bir okla (veya vektörle) temsil edebiliriz. Vektör dikey olarak yukarı doğru ilerlediğinde kubit 0 durumundadır ve vektör dikey olarak aşağı doğru ilerlediğinde kubit 1 durumunda olur. Bu gösterimde klasik bit, her zaman düz yukarı veya aşağı doğru işaret eden ancak hiçbir zaman başka bir yönde olmayan bir vektör olacaktır.
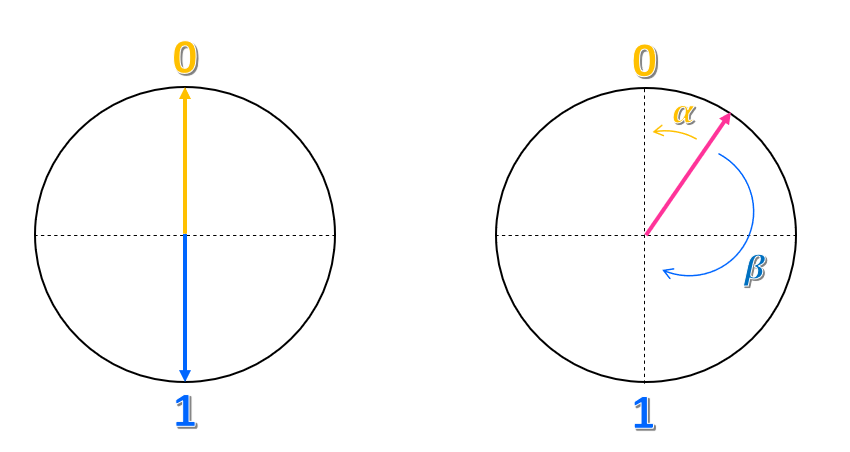
Kubit için vektör dairenin herhangi bir yerine işaret edebilir. Daire üzerindeki her konum, düz yukarı veya düz aşağı dışında bir süperpozisyon durumunu temsil eder. Örneğin, 0 durumu $\alpha$ ile vektör tarafından yapılan açıyı ve 1 durum $\beta$ ile vektör tarafından yapılan açıyı adlandırıyoruz. Ardından kubitin süper konum durumunu $\alpha 0 + \beta 1$ olarak temsil ediyoruz.
Kedi ve kutu örneğine benzer şekilde kubitin süper pozisyon durumu, $\alpha$ ve $\beta$ sayılarıyla ağırlıklandırılmış 0 ve 1 tek tek durumların toplamıdır. Ancak, kedi ve kutu sisteminde ağırlıklar gerçek sayılardır, ancak kubit sisteminde $\alpha$ ve $\beta$ ağırlıkları karmaşık sayılardır.
$\alpha$ ve $\beta$ genlikleri karmaşık sayılar olduğundan, kubitin herhangi bir süper pozisyon durumunu gerçekten temsil etmek için diyagramımızda ilk daireye dik bir düzlemde olan başka bir daireye ihtiyacımız vardır. Bu iki daire Bloch küresini üretmek için üç boyutta bulunur.
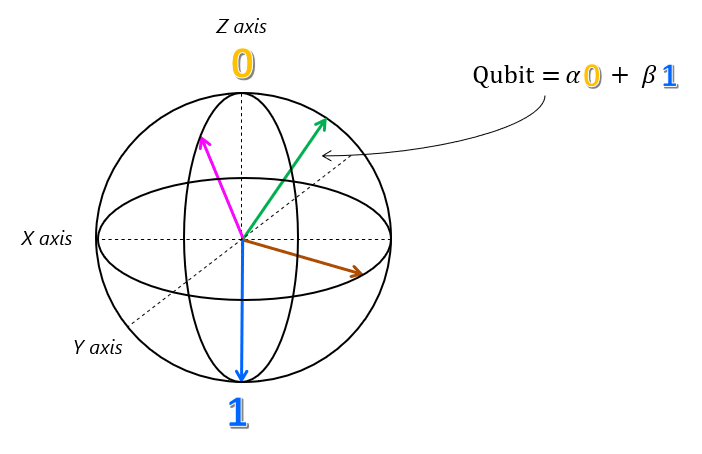
Bu Bloch küresi, tek bir kubit için olası her süper pozisyon durumunun doğru geometrik gösterimidir. Kubit durumu, vektör tarafından işaret edilen kürenin yüzeyindeki konumla temsil edilir. Bloch küresi ne kadar yararlı olsa da, ne yazık ki birden çok kubit içeren sistemlere genişletilemiyor.
İpucu
Kuantum hesaplaması sırasında kubit üzerinde gerçekleştirdiğimiz işlemler Bloch küresinin kardinal eksenlerinden biri hakkında döndürme olarak temsil edildiğinden Bloch küresi güçlü bir araçtır. Bu geometrik gösterim, işlemlerin kuantum bilişiminde nasıl çalıştığı hakkında sezgi oluşturmaya yardımcı olur, ancak algoritmaları tasarlamak ve açıklamak için bu sezgiyi kullanmak zordur. Q# bu tür döndürmeleri açıklamak için bir dil sağlayarak yardımcı olur.
Belirli bir durumda kubit bulma olasılığı nedir?
Önceki ünitedeki kedi ve kutu sisteminde, her durumun ağırlıkları, sistemi her durumda bulma olasılığımıza doğrudan karşılık gelen gerçek sayılardır. Kubit sisteminde $\alpha$ ve $\beta$ sayıları, 0 ve 1 durumlarında kubit bulma olasılığını doğrudan vermeyen genel karmaşık sayılardır. Bunun yerine, bu sayılara olasılık genlikleri (veya yalnızca genlik) denir.
Gerçek olasılıklar, olasılık genliklerinin büyüklüklerinin karelerinden hesaplanır. Ölçümün kubiti 0 durumunda bulma olasılığı $|\alpha|^2$, ölçümün kubiti 1 durumunda bulma olasılığı ise $|\beta|^2$'dır. Genel olarak, $\alpha + \beta$ 100% toplamaz, ancak $|\alpha|^2 + |\beta|^2$ her zaman 100% olur. $|\alpha|^2 + |\beta|^2 = 1$ kısıtlaması normalleştirme koşulu olarak adlandırılır ve her geçerli kuantum durumu bu koşulu karşılamalıdır.