İkili sınıflandırma
Uyarı
Daha fazla ayrıntı için Metin ve resimler sekmesine bakın!
Regresyon gibi sınıflandırma denetimli bir makine öğrenmesi tekniğidir; ve bu nedenle modellerin eğitilmesi, doğrulanması ve değerlendirilmesi için aynı yinelemeli süreci izler. Sınıflandırma modellerini eğitmek için kullanılan algoritmalar, regresyon modeli gibi sayısal değerleri hesaplamak yerine sınıf ataması için olasılık değerlerini ve model performansını değerlendirmek için kullanılan değerlendirme ölçümlerini tahmin edilen sınıfları gerçek sınıflarla karşılaştırır.
İkili sınıflandırma algoritmaları, tek bir sınıf için iki olası etiketlerden birini tahmin eden bir modeli eğitmek için kullanılır. Temelde , doğru veya yanlış tahmin etme. Çoğu gerçek senaryoda, modeli eğitmek ve doğrulamak için kullanılan veri gözlemleri birden çok özellik (x) değerinden ve 1 veya 0 olan bir y değerinden oluşur.
Örnek - ikili sınıflandırma
İkili sınıflandırmanın nasıl çalıştığını anlamak için, y etiketinin 1 mi yoksa 0 mı olduğunu tahmin etmek için tek bir özellik (x) kullanan basitleştirilmiş bir örneğe bakalım. Bu örnekte, hastanın diyabet olup olmadığını tahmin etmek için hastanın kan şekeri düzeyini kullanacağız. Modeli eğiteceğimiz veriler şunlardır:

|

|
|---|---|
| Kan şekeri (x) | Diyabetik? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
İkili sınıflandırma modelini eğitma
Modeli eğitmek için, eğitim verilerini sınıf etiketinin doğru olma olasılığını (başka bir deyişle hastanın diyabete sahip olma olasılığını) hesaplayan bir işleve sığdırmak için bir algoritma kullanacağız. Olasılık, 0,0 ile 1,0 arasında bir değer olarak ölçülür; böylece tüm olası sınıfların toplam olasılığı 1,0 olur. Örneğin, bir hastanın diyabet olma olasılığı 0,7 ise, hastanın diyabetik olmaması olasılığı 0,3'tür.
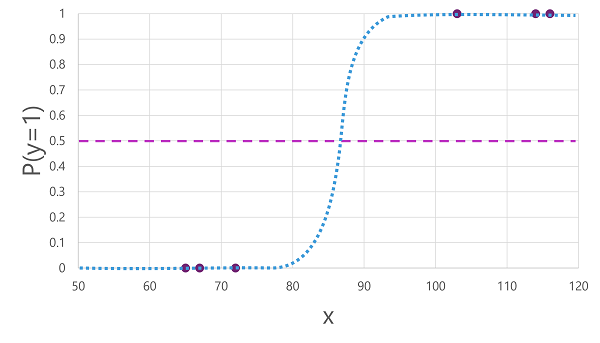
İkili sınıflandırma için kullanılabilecek birçok algoritma vardır, örneğin lojistik regresyon, 0,0 ile 1,0 arasında değerlere sahip S şeklinde bir fonksiyon olan sigmoid işlevini türeten.
Uyarı
Adına rağmen makine öğrenmesinde lojistik regresyon , regresyon için değil sınıflandırma için kullanılır. Önemli nokta, daha düşük ve üst bir değer (ikili sınıflandırma için kullanıldığında 0,0 ve 1,0) arasındaki S şeklindeki eğriyi tanımlayan, ürettiği işlevin lojistik yapısıdır.
Algoritma tarafından üretilen işlev, belirli bir x değeri için y değerinin true (y=1) olma olasılığını açıklar. Matematiksel olarak işlevi şu şekilde ifade edebilirsiniz:
f(x) = P(y=1 | x)
Eğitim verilerindeki altı gözlemden üçü için , y'nin kesinlikle doğru olduğunu biliyoruz, bu nedenle bu gözlemlerin olasılığı y= 1'in 1,0 , diğer üçü için ise y'nin kesinlikle yanlış olduğunu biliyoruz, dolayısıyla y=1'in 0,0 olma olasılığı. S şeklindeki eğri, olasılık dağılımını açıklar, böylece çizgide x değerinin çizildiğinde y'nin1 olma olasılığı tanımlanır.
Diyagram, bu işleve dayalı bir modelin true (1) veya false (0) tahmininde bulunduğu eşiği belirtmek için yatay bir çizgi de içerir. Eşik , y (P(y) = 0,5) için orta noktada bulunur. Bu noktada veya daha yüksek bir noktadaki tüm değerler için model true (1) tahmininde bulunmaya devam eder; bu noktanın altındaki değerler için false (0) tahmin eder. Örneğin, kan şekeri düzeyi 90 olan bir hasta için işlev 0,9 olasılık değerine neden olabilir. 0,9 değeri 0,5 eşiğinden yüksek olduğundan model doğru tahminde bulunur (1) - başka bir deyişle hastanın diyabetli olduğu tahmin edilir.
İkili sınıflandırma modelini değerlendirme
Regresyonda olduğu gibi, ikili sınıflandırma modelini eğitirken, eğitilen modelin doğrulanması için rastgele bir veri alt kümesini tutarsınız. Diyabet sınıflandırıcımızı doğrulamak için aşağıdaki verileri tuttuğumuzu varsayalım:
| Kan şekeri (x) | Diyabetik? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
Daha önce türetdiğimiz lojistik işlevin x değerlerine uygulanması aşağıdaki çizimle sonuçlanır.
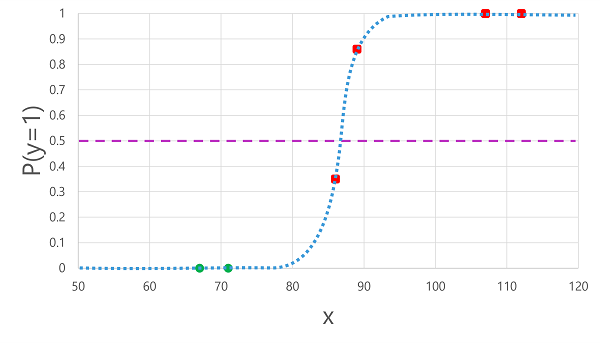
İşlev tarafından hesaplanan olasılığın eşiğin üstünde mi yoksa altında mı olduğuna bağlı olarak model, her gözlem için tahmin edilen 1 veya 0 etiketini oluşturur. Ardından , tahmin edilen sınıf etiketlerini (ŷ) burada gösterildiği gibi gerçek sınıf etiketleriyle (y) karşılaştırabiliriz:
| Kan şekeri (x) | Gerçek diyabet tanısı (y) | Tahmin edilen diyabet tanısı (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
İkili sınıflandırma değerlendirme ölçümleri
İkili sınıflandırma modeli için değerlendirme ölçümlerini hesaplamanın ilk adımı genellikle her olası sınıf etiketi için doğru ve yanlış tahminlerin sayısını içeren bir matris oluşturmaktır:
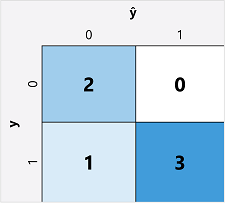
Bu görselleştirme karışıklık matrisi olarak adlandırılır ve tahmin toplamlarını gösterir; burada:
- ŷ=0 ve y=0: Doğru negatifler (TN)
- ŷ=1 ve y=0: Hatalı pozitifler (FP)
- ŷ=0 ve y=1: Hatalı negatifler (FN)
- ŷ=1 ve y=1: Doğru pozitifler (TP)
Karışıklık matrisinin düzeni, doğru (doğru) tahminlerin sol üstten sağ alta doğru çapraz bir çizgide gösterilmesini sağlar. Renk yoğunluğu genellikle her hücredeki tahmin sayısını göstermek için kullanılır, bu nedenle iyi tahminde bulunan bir modele hızlı bir bakış, derin gölgeli çapraz eğilimi ortaya çıkarmalıdır.
Doğruluk
Karışıklık matrisinden hesaplayabileceğiniz en basit ölçüm doğruluk ve modelin doğru tahminlerin oranıdır. Doğruluk şu şekilde hesaplanır:
(TN+TP) ÷ (TN+FN+FP+TP)
Diyabet örneğimizde hesaplama şu şekildedir:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0.83
Bu nedenle doğrulama verilerimiz için diyabet sınıflandırma modeli zamanın 83% doğru tahminler üretti.
Doğruluk başlangıçta modeli değerlendirmek için iyi bir ölçüm gibi görünebilir, ancak bunu göz önünde bulundurun. Popülasyonun 11% diyabet olduğunu varsayalım. Daima 0 sonucunu veren bir model oluşturabilirsiniz ve bu model, hastaların özelliklerini değerlendirerek onları ayırt etmeye çalışmasa da 89%doğruluğa ulaşır. Gerçekten ihtiyacımız olan şey, modelin pozitif vakalar için 1 ve negatif vakalar için 0 tahmininde nasıl performans göstereceğini daha iyi anlamaktır.
Geri çağır
Geri çağırma , modelin doğru şekilde tanımlamış olduğu pozitif vakaların oranını ölçen bir ölçümdür. Başka bir deyişle , diyabeti olan hastaların sayısıyla karşılaştırıldığında, model kaç tane diyabet olduğunu tahmin etti?
Geri çağırma formülü şu şekildedir:
TP ÷ (TP+FN)
Diyabet örneğimiz için:
3 ÷ (3+1)
= 3 ÷ 4
= 0.75
Bu nedenle modelimiz, diyabeti olan hastaların 75% doğru şekilde tanımladı.
Kesinlik
Kesinlik, geri çağırmaya benzer bir ölçümdür, ancak tahmin edilen pozitif vakalar arasında gerçek etiketin pozitif olduğu durumların oranını ölçer. Başka bir deyişle, modelin diyabete sahip olduğu tahmin edilen hastaların hangi oranında gerçekten diyabet var ?
Kesinlik formülü şu şekildedir:
TP ÷ (TP+FP)
Diyabet örneğimiz için:
3 ÷ (3+0)
= 3 ÷ 3
= 1.0
Bu nedenle modelimiz tarafından tahmin edilen hastaların 100% diyabete sahip.
F1 puanı
F1 puanı , geri çekme ve duyarlığı birleştiren genel bir ölçümdür. F1 puanı formülü şöyledir:
(2 x Duyarlık x Geri Çekme) ÷ (Duyarlık + Geri Çekme)
Diyabet örneğimiz için:
(2 x 1.0 x 0.75) ÷ (1.0 + 0.75)
= 1,5 ÷ 1,75
= 0,86
Eğrinin Altındaki Alan (AUC)
Geri çağırmanın diğer adı gerçek pozitif oranı (TPR'dir) ve FP÷(FP+TN) olarak hesaplanan hatalı pozitif oranı (FPR) adlı eşdeğer bir metrik vardır. 0,5 eşiği kullanılırken modelimizin TPR değerinin 0,75 olduğunu zaten biliyoruz ve 0÷2 = 0 değerini hesaplamak için FPR formülünü kullanabiliriz.
Elbette, modelin doğru tahmin ettiği eşiği (1) değiştirirsek, pozitif ve negatif tahminlerin sayısını etkiler; ve bu nedenle TPR ve FPR ölçümlerini değiştirin. Bu ölçümler genellikle 0,0 ile 1,0 arasındaki olası her eşik değeri için TPR ve FPR'yi karşılaştıran bir alınan işleç özelliği (ROC) eğrisi çizilerek modeli değerlendirmek için kullanılır:
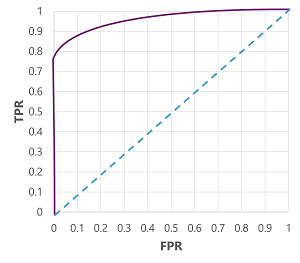
Mükemmel bir model için ROC eğrisi, doğrudan soldaki TPR eksenine ve ardından üstteki FPR eksenine gider. Eğrinin çizim alanı 1x1'i ölçtğından, bu mükemmel eğrinin altındaki alan 1,0 olur (modelin zamanın 100% doğru olduğu anlamına gelir). Buna karşılık, sol alttan sağ üste doğru çapraz çizgi, rastgele bir ikili etiket tahmin edilerek elde edilecek sonuçları temsil eder; 0,5 eğrisi altında bir alan üretir. Başka bir deyişle, iki olası sınıf etiketi göz önünde bulundurulduğunda, zamanın 50% doğru tahminde bulunabilirsiniz.
Diyabet modelimiz söz konusu olduğunda yukarıdaki eğri üretilir ve eğrinin altındaki alan (AUC) 0,875'tir. AUC 0,5'ten yüksek olduğundan, modelin bir hastanın diyabet olup olmadığı konusunda rastgele tahminden daha iyi performans sergilediği sonucuna varabiliriz.