Sınıflandırma nedir?
İkili sınıflandırma, iki kategorili sınıflandırmadır. Örneğin, hastaları diyabetik olmayan veya diyabetik olarak etiketleyebiliriz.
Sınıf tahmini, her olası sınıfın olasılığının 0 (imkansız) ile 1 (belirli) arasında bir değer olarak belirlenmesiyle yapılır. Tüm sınıflar için toplam olasılık her zaman 1'dir, hasta kesinlikle diyabetik veya diyabetik değildir. Bu nedenle, bir hastanın diyabetik olma olasılığı 0,3 ise, hastanın diyabetik olma olasılığı 0,7'dir.
Tahmin edilen sınıfı belirlemek için genellikle 0,5 eşik değeri kullanılır. Pozitif sınıfın (bu örnekte diyabetik) eşikten daha büyük tahmini bir olasılığı varsa, diyabetik sınıflandırması tahmin edilir.
Sınıflandırma modelini eğitma ve değerlendirme
Sınıflandırma, denetimli makine öğrenmesi tekniğinin bir örneğidir ve bu da bilinen özellik değerlerini ve bilinen etiket değerlerini içeren verilere dayalı olduğu anlamına gelir. Bu örnekte özellik değerleri hastalar için tanılama ölçümleridir ve etiket değerleri diyabetik olmayan veya diyabetik olmayanların sınıflandırmasıdır. Sınıflandırma algoritması, verilerin bir alt kümesini özellik değerlerinden her sınıf etiketi için olasılığı hesaplayan bir işleve sığdırmak için kullanılır. Kalan veriler, özelliklerden oluşturduğu tahminleri bilinen sınıf etiketleriyle karşılaştırarak modeli değerlendirmek için kullanılır.
Basit bir örnek
Şimdi temel ilkeleri açıklamaya yardımcı olacak bir örneği inceleyelim. Tek bir özellik (kan şekeri düzeyi) ve diyabetik olmayanlar için 0, diyabetikler için 1 sınıf etiketinden oluşan aşağıdaki hasta verilerine sahip olduğumuzu varsayalım.
| Kan Şekeri | Diyabetik |
|---|---|
| Kategori 82 | 0 |
| 92 | 0 |
| 112 | 1 |
| 102 | 0 |
| 115 | 1 |
| 107 | 1 |
| 87 | 0 |
| 120 | 1 |
| 83 | 0 |
| Kategori 119 | 1 |
| 104 | 1 |
| 105 | 0 |
| 86 | 0 |
| 109 | 1 |
Sınıflandırma modelini eğitmek için ilk sekiz gözlemi kullanırız ve ilk olarak kan şekeri özelliğini (x) ve tahmin edilen diyabetik etiketi (y) çizerek başlarız.
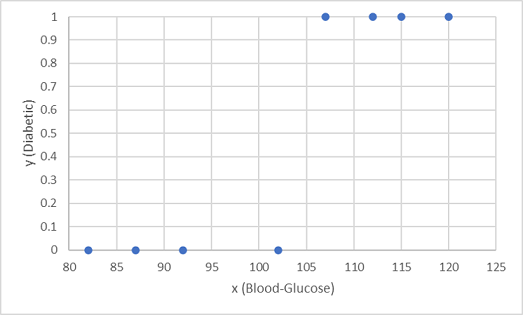
İhtiyacımız olan şey, x'e göre y için bir olasılık değeri hesaplayan bir işlevdir (başka bir deyişle f(x) = y işlevine ihtiyacımız vardır. Grafikten, kan-glikoz düzeyi düşük olan hastaların tümünün diyabetik olmadığını, kan-glikoz düzeyi daha yüksek olan hastaların ise diyabetik olduğunu görebilirsiniz. Kan şekeri düzeyi ne kadar yüksekse, hastanın diyabetik olması o kadar olasıdır ve bükme noktası 100 ile 110 arasında bir yerdedir. y için 0 ile 1 arasında bir değer hesaplayan bir işlevi bu değerlere sığdırmalıyız.
Bu işlevlerden biri, sigmoidal (S şeklinde) eğrisi oluşturan lojistik bir işlevdir.
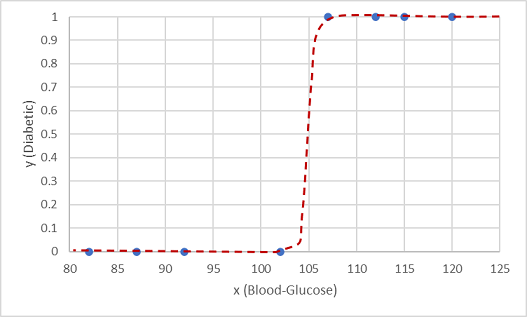
Şimdi işlevi kullanarak y'nin pozitif olduğu, yani hastanın diyabetik olduğu bir olasılık değerini x için işlev satırındaki noktayı bularak herhangi bir x değerinden hesaplayabiliriz. Sınıf etiketi tahmini için kesme noktası olarak 0,5 eşik değeri ayarlayabiliriz.
Bunu, elimizde tuttuğumuz iki veri değeriyle test edelim.
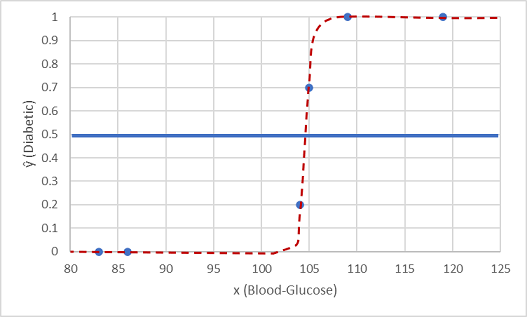
Eşik çizgisinin altına çizilen noktalar tahmin edilen 0 sınıfını (diyabetik olmayan) verir ve çizginin üzerindeki noktalar 1 (diyabetik) olarak tahmin edilir.
Artık modelde kapsüllenen lojistik işlevi temel alarak etiket tahminlerini (ŷ veya "y-hat") gerçek sınıf etiketleriyle (y) karşılaştırabiliriz.
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| Kategori 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |