累积流、提前期和周期时间指南
Azure DevOps Services | Azure DevOps Server 2022 - Azure DevOps Server 2019
使用累积流图(CF)通过系统监视工作流。 可以从图表中提取用于跟踪的两个主要指标、周期时间和潜在顾客时间。 若要配置或查看CFD图表,请参阅 “配置累积流程图”。
或者,可以将潜在顾客时间和周期时间控制图表添加到仪表板。
示例图表和主要指标
连续流CFD提供受遵循精简流程的团队最青睐的图表。
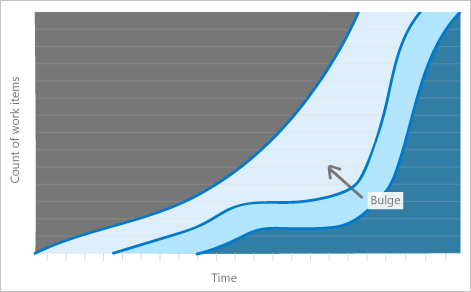
但是,许多团队已经开始将精简做法与 Scrum 或其他方法相结合,这意味着他们在迭代或冲刺的跨度内练习瘦身。 在这种情况下,图表的外观略有不同,并提供另外两个非常有价值的信息,如下一个图表所示。
连续流
此处显示的固定时间段为已完成的冲刺。
上行表示为冲刺设置的范围。 而且,由于工作必须在冲刺的最后一天完成,关闭状态的斜率指示团队是否正轨完成冲刺。 将此视图视为燃烧图的最简单方法。
数据始终被描述为进程中的第一步,作为左上角和进程中的最后一步作为右下角。
修复了已完成冲刺的CFD周期
图表指标
按状态/列随时间推移显示工作项的计数。 可以从图表中提取用于跟踪的两个主要指标、周期时间和潜在顾客时间。
指标
定义
周期时间 1
测量在单个进程或工作流状态中移动工作所需的时间。 计算从一个进程开始到下一个进程的开始。
潜在顾客时间 1
对于连续流过程:测量发出请求(例如添加建议的用户情景)直到该请求完成(已关闭)所花费的时间。
对于冲刺或固定时间段过程:测量从请求的工作开始到工作完成的时间(即从活动到关闭的时间)。
正在进行的工作
度量正在积极工作的工时或工作项的数量。
范围
表示给定时间段内提交的工时量。 仅适用于固定时间段进程。
1 在潜在顾客时间和周期时间上不提供离散数字(分析)和内置的CFD图表(工作跟踪数据存储)。 但是, 潜在顾客时间和周期时间小组件 确实提供这些数字。
潜在时间/周期时间与正在进行的工时(WIP)之间存在明确定义的关联。 WIP 越多,周期时间越长,也会导致提前期更长。 相反的是,WIP 越少,周期越短,领先时间就越短。 当开发团队专注于更少的项目时,它们会减少周期和潜在客户时间。 此关联是可以在开发板上设置工作正在进行限制的关键原因。
工时项计数表示给定一天的总工时量。 在固定期间,此计数的更改指示给定时间段的范围更改。 在连续流CF中,它指示队列中总工时数,并在给定的一天内完成。
将工作分解为特定的板列提供了一个正在处理工作的视图。 此视图提供有关工作顺利进行的位置、存在阻塞和根本没有完成工作的地方的见解。 但是,可视化的CFD图表很难破译数据的表格视图,这提供了一些证据,证明某种事情正在以给定的方式发生。
确定问题,采取适当的操作
在回答几个特定问题时,可以采取操作来调整流程,以便通过系统移动工作。 让我们在这里看看其中每个问题。
团队是否会按时完成工作?
此问题仅适用于固定时间段 CFD。 通过查看开发板最后一列中的工作曲线(或进度)来了解这一点。
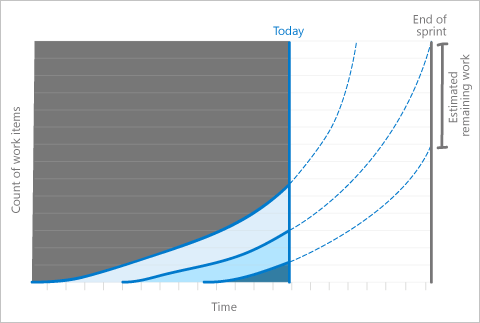
在此方案中,如果很明显,无法以稳定的速度完成工作,那么在迭代中减少工作范围可能合适。 它可能表明工作被低估了,应该纳入下一个冲刺计划。
但是,可以通过查看图表上的其他数据来确定其他原因。
工作进度如何?
团队是否以稳定的速度完成工作? 一种方法是查看图表上不同列之间的间距。 它们与彼此的相似或统一距离是否从头到尾? 某列是否在一段时间内显示为平线? 或者,它似乎“膨胀”了吗?
Mura,平线和凸起的精简术语,意味着不均匀,并指示系统中的一种废物(Muda)。 系统中的任何不均匀性都会导致在CFD中出现凸起。
监视平面线和凸起的CFD支持约束项目管理过程理论的关键部分。 保护系统最慢的区域被称为鼓缓冲绳过程,是计划工作方式的一部分。
两个问题在视觉上显示为平线和凸起。
当团队不定期更新其工作时,将显示平线。 开发 板 提供了将工作从一列转换到另一列的最快方法。
当一个或多个流程的工作花费的时间比计划长时,也可以显示平面线。 平面线显示在系统的许多部分,因为如果系统只有一部分或两个部分存在问题,则会看到一个膨胀。
平线
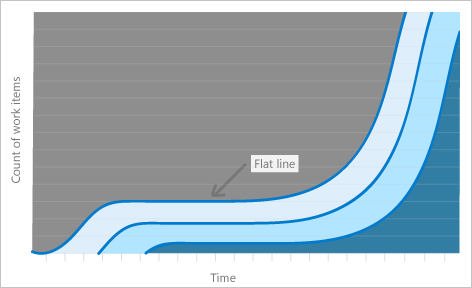
当工作在系统的一部分进行构建并且不会在过程中移动时,会出现浮点。
例如,当测试需要较长时间,而开发需要较短的时间,导致工作累积在开发状态(浮点指示成功步骤出现问题时,不一定是发生膨胀的步骤)时,可能会发生膨胀。
凸起
如何解决流问题?
可以通过以下方法解决缺少及时更新的问题:
- 每日站立。
- 其他常规会议。
- 计划每日团队提醒电子邮件。
系统性平线问题表明一个更具挑战性的问题,尽管这些问题很少见。 平面线表示整个系统的工作已停止。 根本原因可以是:
- 进程范围的阻塞。
- 进程需要很长时间。
- 工作转移到板上未捕获的其他机会。
系统平面线的一个示例可以与特征CFD一起发生。 功能工作花费的时间比处理用户情景要长得多,因为功能由多个故事组成。 在这些情况下,斜率是预期(如上面的示例),或者问题是众所周知的,并且已经由团队提出作为问题。 如果这是一个已知问题,则问题解决超出了本文的范围。
Teams 可以主动修复显示为CFD浮出水面的问题。 根据发生膨胀的位置,修复可能有所不同。 例如,假设在开发过程中出现膨胀。 可能会发生膨胀,因为运行测试花费的时间比编写代码要长得多。 测试人员可能还会发现大量 bug。 当开发人员不断将工作转换回开发人员时,开发人员会继承越来越多的活动工作列表。
解决此问题的两种可能简单方法是:1)将开发人员从开发过程转移到测试过程,直到消除或 2)更改工作顺序,以便可以快速完成的工作与需要更长时间的工作交织在一起。 寻找简单的解决方案来消除浮出水面。
注意
由于许多不同的方案可能会导致工作不均衡地进行,因此必须对问题进行实际分析。 FDA会告诉你,有一个问题,大约在哪里,但你必须调查才能到达根本原因(s)。 此处提供的指南指示建议的操作可以解决特定问题,但可能不适用于你的情况。
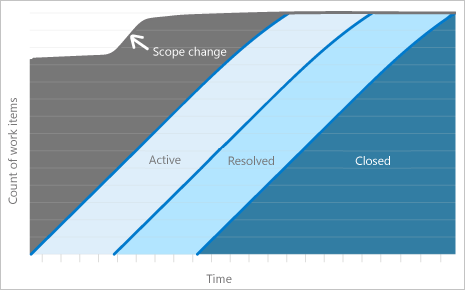
范围是否发生了变化?
范围更改仅适用于固定时间段 CFD。 图表的顶线指示工作范围。 冲刺是预加载工作的第一天。 对上行的更改表示已添加或删除工作。
当在同一天添加相同数量的工作项时,将发生一种方案,即无法跟踪使用CFD的范围更改。 该行将继续平整。 将多个图表与另一个图表进行比较。 监视特定问题。 使用 视图/配置冲刺进度 来监视范围更改。
WIP 太多了?
可以轻松监视 WIP 限制是否已超过开发板。 还可以从FDA 监视它。
大量的 WIP 通常显示为垂直膨胀。 WIP 越多,膨胀就越大,成为椭圆形。 这表明 WIP 对周期和潜在客户产生了负面影响。
下面是正在进行的工作的良好经验法则。 在任何给定时间,每个团队成员最多应该有两个项目正在进行。 两项与更严格的限制的主要原因是现实经常侵入任何软件开发过程。
有时需要时间从利益干系人那里获取信息,或者获取必要的软件需要更多时间。 工作可能停止的原因有多种。 要透视的第二个工作项可提供一些余地。 如果这两个项都被阻止,是时候引发一个红色标志来取消阻止某些内容,而不仅仅是切换到另一个项目。 一旦有大量的项目正在进行,处理这些项目的人员将很难切换上下文。 他们更有可能忘记他们正在做的事情,并可能发生错误。
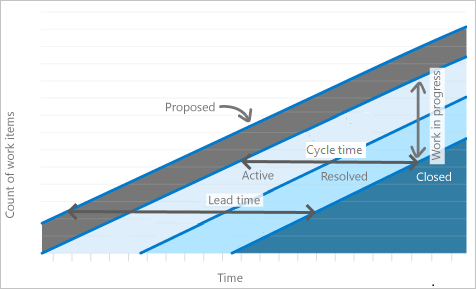
潜在顾客时间与周期时间
下图说明了潜在顾客时间与周期时间有何不同。 从创建工作项到进入“已完成”状态计算潜在顾客时间。 周期时间是从首先输入 “正在进行” 或“ 已解决 ”状态类别到进入 “已完成 ”状态类别计算的。
潜在顾客时间与周期时间图示
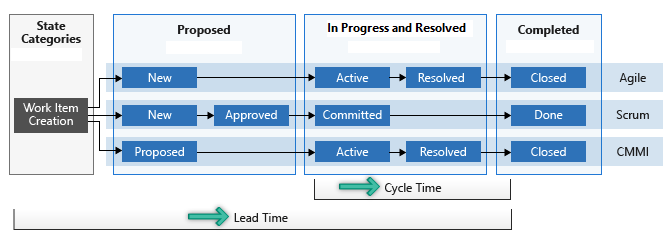
如果工作项进入“已完成”状态,然后重新激活,则在“建议”、“正在进行”或“已解决”状态中花费的任何额外时间都将在第二次进入“已完成”状态类别时,其潜在/周期时间有所贡献。
如果团队使用开发板,则需要了解列如何映射到工作流状态。 有关配置开发板的详细信息,请参阅 “添加列”。
有关系统如何使用状态类别(建议、正在进行、已解决和已完成)的详细信息,请参阅 工作流状态和状态类别。
根据潜在顾客/周期时间使用估算交付时间进行规划
可以使用平均潜在顾客/周期时间和标准偏差来估计交付时间。
创建工作项时,可以使用团队的平均潜在顾客时间估算团队何时完成该工作项。 团队的标准偏差会告诉你估计的可变性。 同样,可以使用周期时间及其标准偏差来估计工作项的完成时间。
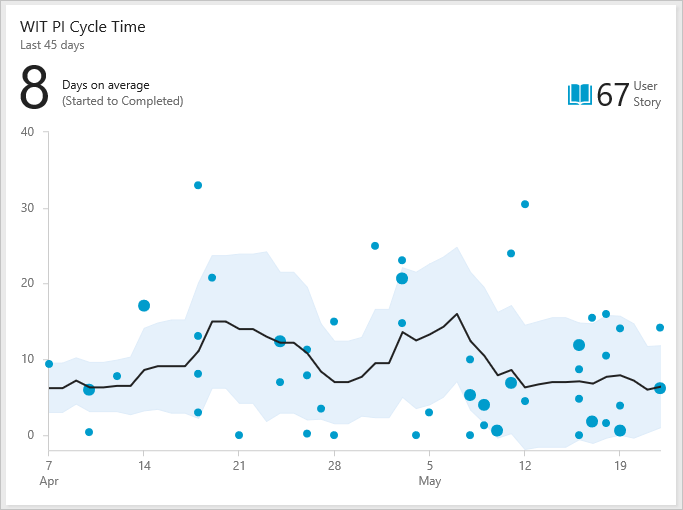
在下图中,平均周期时间为 8 天。 标准偏差为 +/- 6 天。 使用此数据,我们可以估计团队将在工作开始 2-14 天后完成未来的用户情景。 标准偏差越窄,估计越可预测。
周期时间小组件示例
确定进程问题
查看团队的控制图表以获取离群值。 离群值通常表示基础进程问题。 例如,等待太久才能完成 PR 评审或无法快速解决外部依赖项。
如以下图表所示,显示多个离群值,多个 bug 完成时间比团队的平均值要长。 调查这些 bug 花费的时间更长的原因可能有助于发现进程问题。 解决流程问题有助于降低团队的标准偏差并提高团队的可预测性。
显示多个离群值的示例周期时间小组件
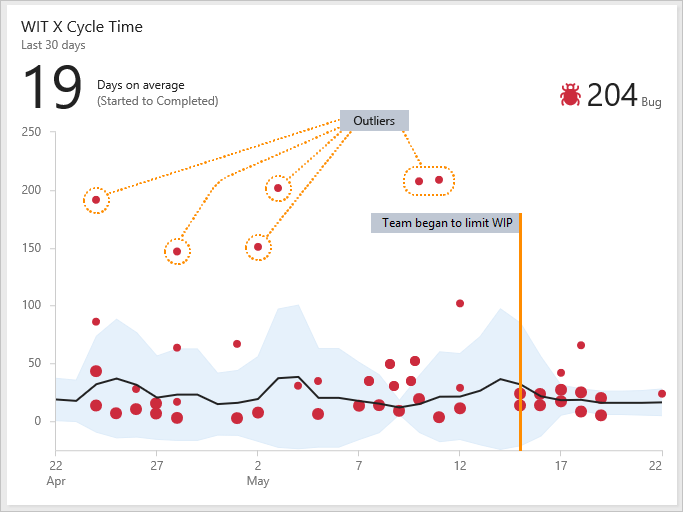
还可以查看流程更改如何影响潜在顾客和周期时间。 例如,在 5 月 15 日,团队齐心协力限制 WIP 并解决过时的 bug。 可以看到标准偏差在该日期后缩小,显示改进的可预测性。