你当前正在访问 Microsoft Azure Global Edition 技术文档网站。 如果需要访问由世纪互联运营的 Microsoft Azure 中国技术文档网站,请访问 https://docs.azure.cn。
使用 Quantum Katas 学习量子计算
ka·ta | kah-tuh
用于学习、练习和实施新技能、方法和流程的模式。
Quantum Katas 是自定进度的开放源代码教程和编程练习,可同时教授量子计算的元素和 Q# 编程语言。 每个 kata 探索量子计算的一项基本概念,其中一些涵盖的是基础知识,而一些是深入探索量子算法和协议。
可以在 Quantum Katas 站点中联机试用 Quantum Katas ,也可以下载 katas 并在计算机上本地运行它们。
提示
若要加速量子计算之旅,检查 Azure Quantum 代码,这是 Azure Quantum网站的独特功能。 在这里,可以运行内置 Q# 示例或自己的 Q# 程序,从提示生成新 Q# 代码,单击一下即可在 VS Code for the Web 中打开并运行代码,并询问 Copilot 有关量子计算的任何问题。
联机运行 Katas
Quantum Katas 可在 Quantum Katas 站点中联机运行。 此环境允许你在浏览器中运行 katas,而无需在计算机上安装任何内容。
Quantum Katas 中收集的教程和练习强调通过积累实践经验来巩固概念学习成果。 编程任务涵盖从非常简单到极具挑战性的各种量子概念。 在每项任务中,都需要填写一些缺失的代码;头几项 kata 可能只要求填写一行,而后面的练习则可能要求填写体量相当大的代码片段。
最重要的是,使用 Quantum Katas,可以在线运行并验证练习的解决方案。 这样你就可以获取解决方案的即时反馈,在其不正确的情况下重新考虑你的方法。
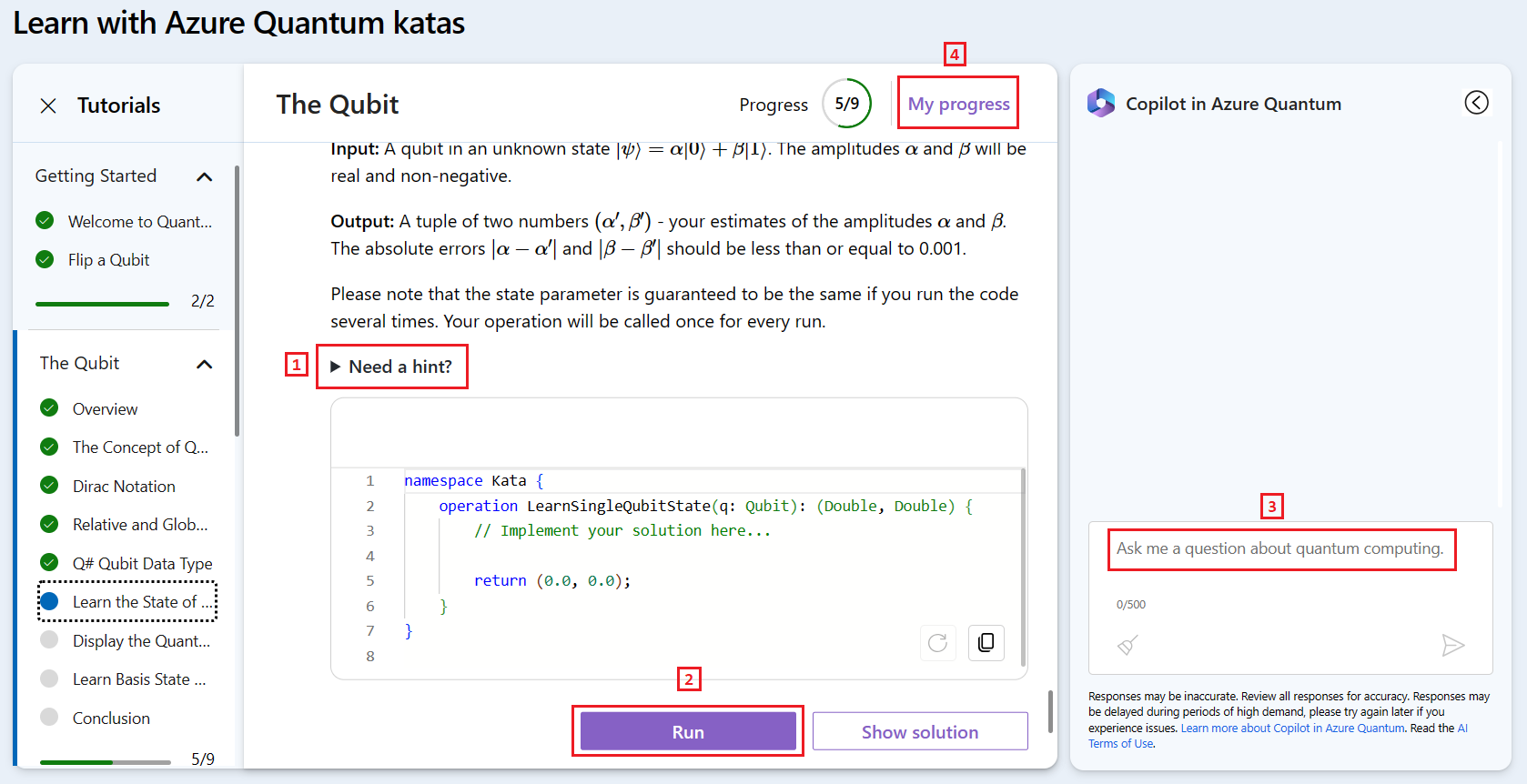
- 如果需要一些帮助,可以单击“ 需要提示?” 获取练习的提示。
- 完成练习后,单击“ 运行 ”按钮以在 kata 中运行代码。 如果遇到问题,可以单击“ 显示解决方案 ”以查看正确的解决方案。
- 随时可以 向 Copilot 询问 有关量子计算或 Q#的问题。
- 可以通过“我的进度”部分中的 Quantum Katas 检查完成率和进度。
反馈
即将发布:在整个 2024 年,我们将逐步淘汰作为内容反馈机制的“GitHub 问题”,并将其取代为新的反馈系统。 有关详细信息,请参阅:https://aka.ms/ContentUserFeedback。
提交和查看相关反馈