矢量、顶点和四元数
顶点会在整个 Direct3D 中描述位置和方向。 基元中的每个顶点都由矢量进行描述,矢量会提供其位置、颜色、纹理坐标和提供其方向的法向矢量。
四元数用于将第四个元素添加到定义三分量矢量的 [x, y, z] 值。 四元数是通常用于 3D 旋转的矩阵方法的替代方法。 四元数表示 3D 空间中的轴和绕该轴的旋转。 例如,四元数可能表示 (1,1,2) 轴和弧度为 1 的旋转。 四元数包含了重要信息,但它们真正的作用来自你可以对其执行的两项运算:合成和内插。
对四元数执行合成与合并它们相似。 两个四元数的合成的符号表示形式与下图相似。
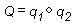
应用于几何图形的两个四元数的组合意味着“通过旋转2围绕轴2旋转几何图形,然后通过旋转1围绕轴1旋转几何图形”。在这种情况下,Q 表示围绕单个轴的旋转,该旋转是向几何图形应用 q2 然后应用 q1 的结果。
利用四元数内插,应用程序可计算出从一个轴和方向到另一个轴和方向的平滑且合理的路径。 因此,q₁ 和 q₂ 之间的内插提供了创建从一个方向到另一个方向的动画的简单方法。
当你将合成和内插一起使用时,它们将为你提供以看起来很复杂的方式操作几何图形的简单方法。 例如,假设你有想要旋转到某个给定方向的几何图形。 你知道你想要绕轴₂将其旋转 r₂ 度,然后绕轴₁将其旋转 r₁ 度,但你不知道最终的四元数。 通过使用合成,你可能将几何图形上的两个旋转组合以获得单个四元数,即结果。 然后,你可能从原四元数内插到合成的四元数以实现从一个四元数到另一个四元数的顺利转换。
相关主题