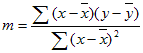WorksheetFunction.LinEst 方法 (Excel)
使用最小平方方法來計算最適合您資料的直線,並傳回描述線條的陣列,以計算線條的統計資料。 因為這個函數傳回的是數值陣列,所以它必須以陣列公式的形態輸入。
語法
運算式。LinEst (Arg1、 Arg2、 Arg3、 Arg4)
表達 代表 WorksheetFunction 物件的 變數。
參數
| 名稱 | 必要/選用 | 資料類型 | 描述 |
|---|---|---|---|
| Arg1 | 必要 | Variant | Known_y的 - 您在關聯性 y = mx + b 中已經知道的 y 值集合。 |
| Arg2 | 選用 | Variant | Known_x's - y = mx + b 關係式中已知的一組選擇性 x 值。 |
| Arg3 | 選用 | Variant | Const - 邏輯值,指定是否強制常數 b 等於 0。 |
| Arg4 | 選用 | Variant | Stats - 指定是否要傳回其他迴歸統計資料的邏輯值。 |
傳回值
Variant
註解
如果有多個範圍的 x 值) ,則線條的方程式為 y = mx + b 或 y = m1x1 + m2x2 + ... + b (,其中相依的 y 值是獨立 x 值的函式。 m 值是對應至每個 x 值的係數,而 b 是常數值。 請注意,y、x 與 m 可以為向量。 LinEst傳回的陣列為 {mn,mn-1,...,m1,b} 。 LinEst 也可以傳回其他回歸統計資料。
如果陣列known_y位於單一資料行中,則known_x的每個資料行都會解譯為個別的變數。
如果陣列known_y位於單一資料列中,則known_x的每個資料列都會解譯為個別的變數。
known_x's 陣列可能含有一組或多組變數。 如果只用到一個變數,known_y's 與 known_x's 可以是任何形狀的範圍,只要兩者有相同的維數即可。 如果有多個變數,則 known_y's 陣列必須是向量 (也就是高度為一列或寬度為一欄的範圍)。
如果省略known_x,則會假設其為 {1,2,3,...} 與known_y大小相同的陣列。
如果 const 為 True 或省略,則會正常計算 b。
如果 const 為False,b 會設定為等於 0,並調整 m 值以符合 。
y = mx如果統計資料為 True, LinEst 會傳回其他回歸統計資料,因此傳回的陣列為
{mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}。如果統計資料為 False 或省略, LinEst 只會傳回 m 係數和常數 b。
額外的迴歸統計資料如下:
| 回歸統計資料 | 描述 |
|---|---|
| se1,se2,...,sen | 係數 m1,m2,...,mn 的標準誤差。 |
| Seb | 當 const 為 False) 時,常數 b (seb = #N/A 的標準錯誤值。 |
| R 2 | 判定係數。 比較 y 的實際值與估計值,其值的範圍從 0 到 1。 如果是 1,則範例中有完美的相互關聯—估計的 y 值與實際的 y 值之間沒有任何差異。 另一方面,如果判定係數是 0,迴歸方程式對預測 y 數值便沒有幫助。 |
| sey | 對於 y 估計值的標準誤差。 |
| F | F 統計值或 F 觀察值。 F 統計值常用來決定自變數和因變數間的關係是否是巧合的。 |
| Df | 自由度。 使用自由度可幫助您於統計的表格中找出 F 臨界值。 比較您在資料表中找到的值與 LinEst 傳回的 F 統計資料,以判斷模型的信賴等級。 |
| ssreg | 迴歸平方和。 |
| ssresid | 殘差平方和。 |
下列圖例顯示傳回額外的迴歸統計資料的順序。
您可以使用斜率和 Y 截距來描述任何直線: Slope (m) 。 若要尋找通常以 m 撰寫的線條斜率,請在行上取得兩個點: (x1,y1) 和 (x2,y2) ;斜率等於 (y2 - y1) / (x2 - x1) 。 Y 截距 (b) :線條的 Y 截距通常寫成 b,是線條與 y 軸交叉點的 y 值。 直線的方程式為 y = mx + b。 在您知道 m 和 b 的值之後,您可以將 y 或 x 值插入該方程式,以計算行上的任何點。 您也可以使用 TREND 函式。
當您只有一個獨立的 x 變數時,可以使用下列公式直接取得斜率和 Y 攔截值:
- 邊坡:
=INDEX(LINEST(known_y's,known_x's),1) - Y 攔截:
=INDEX(LINEST(known_y's,known_x's),2)
LinEst所計算行的精確度取決於資料中的散佈程度。 資料越線性, LinEst 模型就越精確。 LinEst 會使用最小平方的 方法來判斷最適合的資料。 當您只有一個獨立的 x 變數時,m 和 b 的計算會以下列公式為基礎:
表示 x 和 y 是範例表示,也就是 x = AVERAGE (已知 x 的) 和 y = AVERAGE (known_y的) 。
線條和曲線調整函式 LinEst 和 LogEst 可以計算最適合您資料的直線或指數曲線。 不過,您必須自己決定那個結果最適合於您的資料使用。 您可以計算 TREND(known_y's,known_x's) 直線或 GROWTH(known_y's, known_x's) 指數曲線。 在沒有 new_x's 引數時,它們會傳回根據自變數 x 所預測的 y 估計值陣列。 然後您就可以比較預測的數值和確實的數值。 您亦可以繪成圖表以視覺比較其差異。
在 迴歸分析中,Microsoft Excel 會計算該點預估的 y 值與其實際 y 值之間的平方差異。 這些平方差異的總和稱為正方形的剩餘總和 ssresid。 Excel 接著會計算平方的總和 sstotal。 當 const = TRUE 或省略時,平方的總和是實際 y 值與 y 值平均值之間的平方差異總和。 當 const = FALSE 時,平方的總和是實際 y 值 (的平方總和,而不會從每個個別的 y 值減去平均 y 值) 。 然後可以從 ssreg = sstotal - ssresid 找到方形的回歸總和 ssreg。 相較于平方的總和,剩餘的平方總和越小,判斷係數 r2 的值愈大,這是迴歸分析所產生方程式如何說明變數之間關聯性的指標;r2 等於 ssreg/sstotal。
在某些情況下,一或多個 X 資料行 (假設 Y 和 X 位於資料行中,) 可能沒有其他 X 資料行存在的額外預測值。 換句話說,刪除一個或多個 X 欄可能會得到一樣精確的預測 Y 值。 在此情況下,應該從回歸模型中省略這些備援 X 資料行。 這種現象稱為 共線性 ,因為任何多餘的 X 資料行都可以表示為非備援 X 資料行的倍數總和。 LinEst 會檢查共線性,並在識別回歸模型時,從回歸模型中移除任何多餘的 X 資料行。 已移除的 X 資料行可在 LinEst 輸出中辨識為具有 0 個係數以及 0 個 se。
- 如果將一或多個資料行移除為備援,df 會受到影響,因為 df 取決於實際用於預測用途的 X 資料行數目。 如果自由度因移除多餘的 X 欄而變更,也會連帶影響 sey 值及 F。
- 共線性在實際上應該是很少見的。 不過,其中一個比較可能發生的情況是,某些 X 資料行只包含 0 和 1 作為實驗中主體是否為特定群組成員的指標。 如果 const = TRUE 或省略, LinEst 會 有效地插入所有 1 的額外 X 資料行來建立截距模型。 如果您有一個資料行,如果是 male,則每個主旨都有一個 1 的資料行,如果為 0,而且如果是女性,則每個主旨也有一個 1 的資料行,如果沒有,則這個後一個資料行是多餘的,因為其中的專案可以從LinEst新增之所有 1 的額外資料行中減去男性指針資料行中的專案來取得。
- 當由於共線性而未從模型中移除任何 X 資料行時,df 的計算方式如下:如果有 k 個數據行的 known_x 和 const = TRUE 或省略,則
df = n - k - 1為 。 如果 const = FALSE,則為df = n - k。 在這 2 個例子中,因為共線性增加 1 個單位的自由度,而會移除每個 X 欄。
傳回陣列的公式必須輸入為陣列公式。
- 當類似 known_x's 的陣列常數以引數的形式輸入時,請使用逗點 (,) 來區隔同列中的值,並以分號 (;) 來區隔不同列。 分隔符號字元可能會依據您在 [控制台] 中 [地區及語言選項] 內的地區設定而有所不同。
- 您應該注意由迴歸方程式所求得的 y 估計值,如果他們超出您用以計算迴歸直線方程式的 y 實際值範圍,則 y 估計值可能不正確。
LinEst函式中使用的基礎演算法與Slope和Intercept函式中使用的基礎演算法不同。 當資料為未確定或共線的資料時,這些演算法之間的差異可能會導致不同的結果。 例如,如果 known_y's 引數的資料點為 0,而且 known_x's 引數的資料點為 1:
- LinEst 會傳回值 0。 LinEst演算法的設計目的是要傳回適用于共線性資料的合理結果,在此情況下,至少可以找到一個答案。
- 斜率 和 截距 會傳回 #DIV/0! 錯誤。 斜率和截距演算法的設計目的是要尋找一個答案,而且在此情況下可以有一個以上的答案。
支援和意見反應
有關於 Office VBA 或這份文件的問題或意見反應嗎? 如需取得支援服務並提供意見反應的相關指導,請參閱 Office VBA 支援與意見反應。