多類別分類
多類別分類 可用來預測觀察所屬多個可能類別的哪一個。 作為受監督的機器學習技術，它會遵循與回歸和二元分類相同的反覆 定型、驗證和評估 程式，在其中保留定型數據的子集來驗證定型模型。
範例 - 多類別分類
多類別分類演算法可用來計算多個類別標籤的機率值，讓模型能夠預測指定觀察 的可能 類別。
讓我們來探索一個範例，其中我們擁有一些關於企鵝的觀察，並記錄每隻企鵝的翼長（x）。 針對每個觀察，數據包含企鵝物種（y），其編碼方式如下：
- 0：阿黛莉
- 1：根多
- 2： 欽斯特拉普
備註
如同本課程模組中先前的範例，實際案例會包含多個功能 （x） 值。 我們將使用單一功能讓事情保持簡單。
|
|
|---|---|
| 翻轉器長度 （x） | 物種 （y） |
| 167 | 0 |
| 172 | 0 |
| 225 | 2 |
| 197 | 1 |
| 189 | 1 |
| 232 | 2 |
| 158 | 0 |
定型多類別分類模型
若要定型多類別分類模型，我們需要使用演算法，將定型數據放入計算每個可能類別之機率值的函式。 有兩種演算法可用來執行這項作：
- One-vs-Rest （OvR） 演算法
- 多項演算法
One-vs-Rest （OvR） 演算法
One-vs-Rest 演算法會為每個類別定型二元分類函數，每個演算法都會計算觀察是目標類別範例的機率。 每個函式都會計算與 任何其他 類別相比，觀察為特定類別的機率。 對於我們的企鵝物種分類模型，演算法基本上會建立三個二元分類函式：
- f0（x） = P（y=0 | x）
- f1（x） = P（y=1 | x）
- f2（x） = P（y=2 | x）
每個演算法都會產生 sigmoid 函式，以計算介於 0.0 和 1.0 之間的機率值。 使用這種演算法定型的模型會預測產生最高機率輸出之函式的 類別。
多項演算法
另一種方法是使用多項演算法，這會建立傳回多重值輸出的單一函式。 輸出是一個 向量 （值陣列），其中包含所有可能類別的 機率分佈 - 每個類別的機率分數總計最多為1.0：
f（x） =[P（y=0|x）， P（y=1|x）， P（y=2|x）]
這類函式的範例是 softmax 函式，可能會產生如下列範例所示的輸出：
[0.2, 0.3, 0.5]
向量中的元素分別代表類別 0、1 和 2 的機率：因此，在此情況下，機率最高的類別為 2。
不論使用哪種演算法類型，模型都會使用產生的函式來判斷指定一組特徵 （x） 的最可能類別，並預測對應的類別標籤 （y）。
評估多類別分類模型
您可以計算每個個別類別的二元分類計量，以評估多類別分類器。 或者，您可以計算將所有類別納入考慮的匯總計量。
假設我們已驗證多類別分類器，並取得下列結果：
| 翻轉器長度 （x） | 實際物種 （y） | 預測物種 （ŷ） |
|---|---|---|
| 165 | 0 | 0 |
| 171 | 0 | 0 |
| 205 | 2 | 1 |
| 195 | 1 | 1 |
| 183 | 1 | 1 |
| 221 | 2 | 2 |
| 214 | 2 | 2 |
多類別分類器的混淆矩陣與二元分類器的混淆矩陣類似，不同之處在於它會顯示 預測 的每個組合 （ŷ） 和 實際 類別卷標的預測數目 （y）：
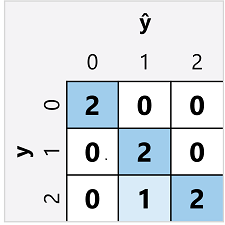
在此混淆矩陣中，我們可以判斷每個個別類別的計量，如下所示：
| 班級 | 衛生紙 | TN | Functional Programming (if "FP" stands for this, the translation would be 功能性程式設計) | FN | 準確性 | 召回 | 精確度 | F1-Score |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 5 | 0 | 0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 1 | 2 | 4 | 1 | 0 | 0.86 | 1.0 | 0.67 | 0.8 |
| 2 | 2 | 4 | 0 | 1 | 0.86 | 0.67 | 1.0 | 0.8 |
若要計算整體精確度、召回率和精確度計量，您可以使用 TP、 TN、 FP 和 FN 計量總計：
- 整體精確度 = （13+6）÷（13+6+1+1） = 0.90
- 整體召回 率 = 6÷（6+1） = 0.86
- 整體精確度 = 6÷（6+1） = 0.86
整體 F1 分數是根據整體召回率和準確度來計算的。
- 整體 F1 分數 = （2x0.86x0.86）÷（0.86+0.86） = 0.86