評估不同類型的叢集
定型叢集模型
您可以使用多個演算法來進行叢集。 其中一個最常用的演算法是「K-Means」叢集,在其最簡單的格式中包含下列步驟:
- 特徵值會向量化以定義 n 維座標(其中 n 是特徵數目)。 在花朵範例中有兩個特徵:花瓣數目和葉子數目。 特徵向量有兩個座標,我們可以使用這兩個座標,在二維空間中繪製資料點的概念圖。
- 您決定要用來分組花朵的叢集數目 - 呼叫此值 k。 例如,若要建立三個叢集,您會使用 k 值 3。 然後以隨機座標繪製 k 點。 這些點會是每個叢集的中心點,因此稱為「形心」。
- 每個資料點 (在此案例中是指花卉) 會指派至其最近的形心。
- 每個形心都會根據點之間的平均距離,移至指派給它的資料點中心。
- 移動形心之後,資料點現在可能更接近不同的形心,因此會根據最近的新形心將資料點重新指派給叢集。
- 形心移動和叢集重新配置步驟會重複,直到叢集變成穩定或達到預先決定的反覆運算次數上限為止。
下圖顯示此流程:

階層式叢集
階層式叢集是另一種類型的叢集演算法,其中叢集本身屬於更大的群組,該群組又屬於更大的群組,依此類推。 結果就是資料點可以是不同的精確程度的叢集:有大量的非常小且精確的群組,或少數的較大群組。
例如,如果將叢集應用於字詞意義,我們可能會得到一組含有專指情緒的形容詞組 (例如「生氣」、「快樂」等)。 此群組屬於包含所有人類相關形容詞 (「快樂」、「英俊」、「年輕」) 的群組,其屬於包含所有形容詞 (「快樂」、「生澀」、「英俊」、「困難」等) 的更高群組。
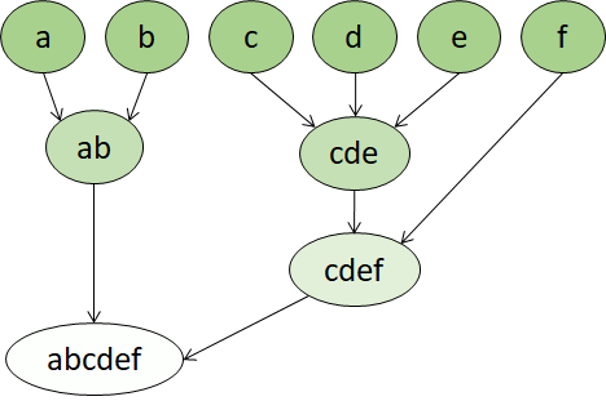
階層式叢集對於不只是將資料分成多個群組,還有了解這些群組之間的關聯性,都很有用。 階層式叢集的主要優點,就是不需要事先定義叢集的數目。 與非階層式的方法相比,此方法有時能夠提供更具解釋性的結果。 最大的缺點是,這些方法所花費的時間比起較為簡單的方法可能更長,有時不適合大型資料集。