何謂迴歸?
迴歸的作業方式是在資料中的變數之間建立關聯性,該資料代表所觀察項目的特性 (稱為特徵),以及我們嘗試預測的變數 (稱為標籤)。
回想一下之前的出租自行車公司,該公司想要預測某一天會有多少預期的租用數量。 在這個案例中,特徵包括星期幾、月份等項目,標籤則是自行車租用數量。
若要對模型進行定型,我們會從包含特徵和已知標籤值的資料範例開始著手;因此在本案例中,我們需要歷史資料,其中包括日期、天氣狀況以及自行車租借的次數。
接著,我們會將此資料範例分割成兩個子集:
- 「定型」資料集,其中我們將套用某個演算法,以判斷封裝特徵值和已知標籤值之間關聯性的函式。
- 「驗證」或「測試」資料集,我們可以使用此資料集來產生標籤預測,並將其與實際已知標籤值進行比較來評估模型。
由於迴歸會使用具有已知標籤值的歷程資料將模型定型,使其成為「監督式」機器學習的範例之一。
簡單範例
我們來看一個簡單的範例,了解定型和評估程序的工作原理。 假設我們將案例簡化,使用單一特徵 (每日平均溫度) 來預測自行車租借標籤。
我們可以從某些資料,包括每日平均溫度特徵和自行車租借標籤的已知值開始著手。
| 溫度 | 租用數量 |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
| 82 | 156 |
| 54 | 114 |
| 62 | 129 |
現在,我們將隨機選取其中五個觀察值,並使用它們來定型迴歸模型。 當我們提到「對模型進行定型」時,我們的意思是找出函式 (某個數學方程式;讓我們將其稱為 f),以使用溫度特徵 (讓我們將其稱為 x) 來計算租用數量 (讓我們將其稱為 y)。 換句話說,我們必須定義下列函式:f(x) = y。
我們的定型資料集看起來像這樣:
| x | y |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
首先,讓我們在圖表上為 x 和 y 繪製定型值:

接下來,我們需要將這些值納入函式中,並允許一些隨機變化發生。 您可能會看到繪圖點形成幾乎直線的對角線,換句話說,在 x 和 y 之間存在明顯的「線性」關聯,因此我們需要尋找最適合資料範例的線性函式。 判斷本函式的演算法有許多種,這些方法最終將會尋找到從繪圖點具有最小整體變異數的一條直線,例如:
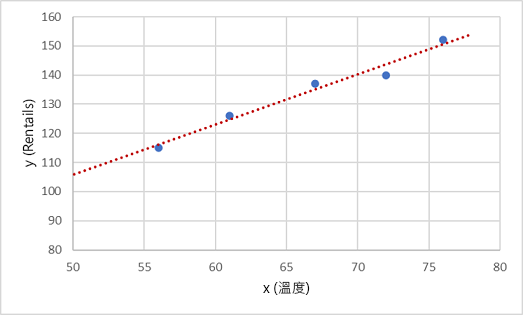
這條線代表可搭配任何 x 值使用的線性函式,以套用線的「斜率」以及其「截距」 (當 x 為 0 時線與 y 軸交叉的位置),來計算 y。 在此案例中,如果我們將此線延伸至左方,我們會發現當 x 為 0 時,y 大約為 20,而線的斜率則表示在 x 上每向右側移動一個單位時,y 會增加大約 1.7。 因此,我們可以將 f 函式計算為 20 + 1.7x。
既然我們已定義預測函式,我們可以加以用來預測我們所保留的驗證資料的標籤,並將預測值 (這通常是以符號 ŷ 或 "y-hat" 表示) 與實際已知的 y 值互相比較。
| x | y | ŷ |
|---|---|---|
| 82 | 156 | 159.4 |
| 54 | 114 | 111.8 |
| 62 | 129 | 125.4 |
我們來看 y 和 ŷ 值在繪圖中的比較:
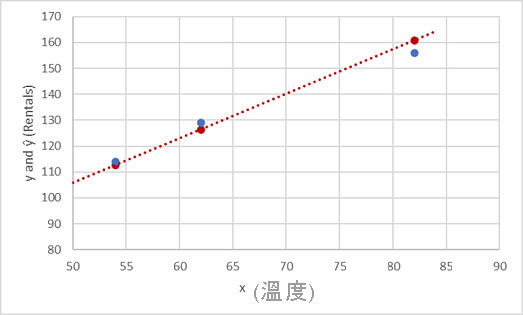
在函式線上繪製的點是由函式所計算的預測 ŷ 值,而其他繪製的點則是實際的 y 值。
有多種方式可以計量預測值和實際值之間的變異數,而且我們可以使用這些計量來評估模型的預測程度。
注意
機器學習是以統計資料和數學為基礎,因此請務必留意統計學家和數學家 (當然還有資料科學家) 使用的特定字詞。 您可以將「預測」標籤值與「實際」標籤值之間的差數視為「錯誤」的量值。 不過,在實務上,「實際」值是以範例觀察 (其本身可能會受到某些隨機變異數的影響) 為基礎。 為了清楚說明我們所比較的是「預測」值 (ŷ) 與「觀察」值 (y),我們將其差異稱為「殘差值」。 我們可以彙總所有驗證資料預測的殘差值,以計算模型中的整體「損耗」,並作為其預測效能的量值。
測量遺失最常見的方式之一,就是求個別的殘差值平方、加總平方和計算平均值。 求殘差值平方能使計算以「絕對」值 (忽略差數是否為正數或負數) 為基礎,並為較大的差數提供更多權數。 此計量稱為「平均平方誤差」。
針對我們的驗證資料,計算如下所示:
| y | ŷ | y - ŷ | (y - ŷ)阿拉伯數位 |
|---|---|---|---|
| 156 | 159.4 | -3.4 | 11.56 |
| 114 | 111.8 | 2.2 | 4.84 |
| 129 | 125.4 | 3.6 | 12.96 |
| Sum | ∑ | 29.36 | |
| 平均數 | x̄ | 9.79 |
因此,我們以 MSE 計量為基礎之模型的損耗為 9.79。
這代表好或壞呢? 很難分辨,因為 MSE 值並不是以有意義的測量單位表示。 我們知道值越低,代表模型中的損耗就越少,因此預測的效果也越好。 這使其成為比較兩個模型,並找出其中效能較佳之模型的實用計量。
有時候,以和預測標籤值本身相同的測量單位 (在本案例中為租用數量) 來表達損耗會更實用。 您可以透過計算 MSE 的平方根來完成此作業;不意外地,其會產生稱為「均方根誤差」(RMSE) 的計量。
√9.79 = 3.13
我們的模型中的 RMSE 指出損耗僅大於 3 一點點,因此您可以大致將其視為平均而言,不正確預測的誤差大概是三個租用數量。
此外,還有許多其他計量可用來測量迴歸中的遺失。 例如,R2 (R 平方) (有時也稱為「決定係數」),是 x 和 y 平方之間的相互關聯。 這會產生介於 0 和 1 之間的值,以測量模型可說明的變異數量。 一般來說,這個值越接近 1,模型就能越精準地預測。