Přehled transformace

Maticové transformace zpracovávají většinu nízkoúrovňové matematiky 3D grafiky.

Geometrický kanál přebírá vrcholy jako vstup. Transformační modul aplikuje transformace světa, zobrazení a projekce na vrcholy, ořízne výsledky a předá je rasterizátoru.

Transformace a prostor	Popis
Souřadnice modelu v prostoru modelu	V čele potrubí jsou vrcholy modelu deklarovány vzhledem k místnímu souřadnicovému systému. Jedná se o místní původ a orientaci. Tato orientace souřadnic se často označuje jako prostor modelu . Jednotlivé souřadnice se nazývají souřadnice modelu .
Svět se transformuje do světa vesmíru	První fáze geometrického potrubí transformuje vrcholy modelu z jejich místního souřadnicového systému na souřadnicový systém, který používají všechny objekty ve scéně. Proces přeorientování vrcholů se nazývá transformace světa, která převádí z modelového prostoru na novou orientaci zvanou prostor světa. Každý vrchol ve světě vesmíru je deklarován pomocí souřadnic světa.
Transformace do prostoru zobrazení (prostor kamery)	V další fázi jsou vrcholy, které popisují váš 3D svět, orientované na kameru. To znamená, že vaše aplikace zvolí pro scénu bod zobrazení a souřadnice světových prostorů se přemístí a otočí kolem zobrazení kamery a změní prostor světa na prostor zobrazení (označuje se také jako prostor kamery ). Toto je transformace Zobrazení, která převádí z prostoru světa do prostoru zobrazení.
Projekce se transformuje na prostor projekce	Další fází je transformace Projekce, která převádí z oblasti zobrazení na prostor projekce. V této části potrubí jsou objekty obvykle škálovány s ohledem na jejich vzdálenost od diváka, aby poskytly iluzi hloubky ve scéně; blízké objekty se zobrazují větší než vzdálené objekty. Pro zjednodušení tato dokumentace odkazuje na prostor, ve kterém se nacházejí vrcholy po projekční transformaci, jako prostor projekce. Některé grafické knihy mohou odkazovat na projekční prostor jako post-perspektivní homogenní prostor. Ne všechny projekce transformují měřítko velikosti objektů ve scéně. Projekce, jako je tato, se někdy označuje jako afinní nebo ortogonální projekce.
Výřez v prostoru obrazovky	V poslední části potrubí se odeberou všechny vrcholy, které na obrazovce nebudou viditelné, aby se rastrovač nezabýval výpočtem barev a stínování pro něco, co se nikdy nezobrazí. Tento proces se nazývá ořez. Po výřezu se zbývající vrcholy škálují podle parametrů zobrazení a převádějí se na souřadnice obrazovky. Výsledné vrcholy, které se zobrazují na obrazovce, když je scéna rasterizována, existují v prostoru obrazovky.

 

Transformace se používají k převodu geometrie objektu z jednoho prostoru souřadnic na jiný. Direct3D používá matice k provádění 3D transformací. Matice vytvářejí 3D transformace. Matice můžete kombinovat a vytvořit jednu matici, která zahrnuje více transformací.

Můžete převádět souřadnice mezi prostorem modelu, světovým prostorem a zobrazeným prostorem.

• Transformace do světového prostoru – převádí z modelového prostoru do světového prostoru.
• Převod pohledu – převádí ze světa do prostoru zobrazení.
• Transformace projekce – převod z prostoru zobrazení na prostor projekce.

Transformace matice

V aplikacích, které pracují s 3D grafikou, můžete pomocí geometrických transformací provést následující akce:

• Umožňuje vyjádřit umístění objektu vzhledem k jinému objektu.
• Otočit a změnit velikost objektů
• Změňte zobrazení pozic, směrů a perspektiv.

Libovolný bod (x,y,z) můžete transformovat na jiný bod (x', y', z) pomocí matice 4x4, jak je znázorněno v následující rovnici.

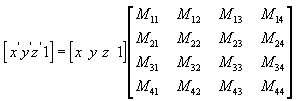
Pomocí následujících rovnic (x, y, z) a matice vytvořte bod (x', y', z').

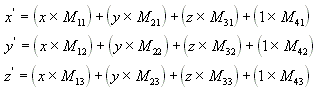
Nejběžnějšími transformacemi jsou překlad, otočení a škálování. Matice, které tyto efekty vytvářejí, můžete zkombinovat do jedné matice a vypočítat několik transformací najednou. Můžete například vytvořit jednu matici, která přeloží a otočí řadu bodů.

Matice se zapisují v pořadí řádků a sloupců. Matice, která rovnoměrně škáluje body podél každé osy, nazývané jednotným škálováním, je reprezentována následující maticí pomocí matematického zápisu.

V jazyce C++ Direct3D deklaruje matice jako dvojrozměrné pole pomocí struktury matice. Následující příklad ukazuje, jak inicializovat strukturu D3DMATRIX tak, aby fungovala jako jednotná matice škálování (koeficient "s").

D3DMATRIX scale = {
    5.0f,            0.0f,            0.0f,            0.0f,
    0.0f,            5.0f,            0.0f,            0.0f,
    0.0f,            0.0f,            5.0f,            0.0f,
    0.0f,            0.0f,            0.0f,            1.0f
};

Překlad

Následující rovnice přeloží bod (x, y, z) na nový bod (x', y', z').

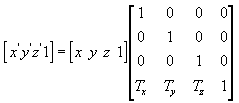
Matici překladu můžete vytvořit ručně v jazyce C++. Následující příklad ukazuje zdrojový kód pro funkci, která vytvoří matici pro překlad vrcholů.

D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
    D3DXMATRIX ret;

    D3DXMatrixIdentity(&ret);
    ret(3, 0) = dx;
    ret(3, 1) = dy;
    ret(3, 2) = dz;
    return ret;
}    // End of Translate

škálování

Následující rovnice škáluje bod (x, y, z) libovolnými hodnotami ve směru x-, y a z na nový bod (x', y', z').

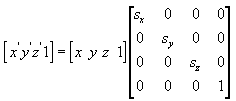
otočit

Zde popsané transformace jsou určené pro levoruké souřadnicové systémy, takže se můžou lišit od transformačních matic, které jste viděli jinde.

Následující rovnice otočí bod (x, y, z) kolem osy x a vytvoří nový bod (x', y', z').

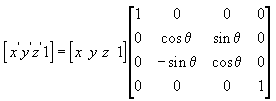
Následující rovnice otočí bod kolem osy y.

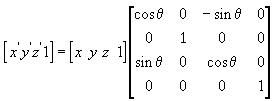
Následující rovnice otočí bod kolem osy z.

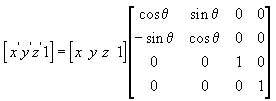
V těchto ukázkových maticích je řecké písmeno theta zkratkou pro úhel otáčení v radiánech. Úhly se měří po směru hodinových ručiček při pohledu podél osy otáčení směrem k počátku.

Následující kód ukazuje funkci pro zpracování otočení o ose X.

    // Inputs are a pointer to a matrix (pOut) and an angle in radians.
    float sin, cos;
    sincosf(angle, &sin, &cos);  // Determine sin and cos of angle

    pOut->_11 = 1.0f; pOut->_12 =  0.0f;   pOut->_13 = 0.0f; pOut->_14 = 0.0f;
    pOut->_21 = 0.0f; pOut->_22 =  cos;    pOut->_23 = sin;  pOut->_24 = 0.0f;
    pOut->_31 = 0.0f; pOut->_32 = -sin;    pOut->_33 = cos;  pOut->_34 = 0.0f;
    pOut->_41 = 0.0f; pOut->_42 =  0.0f;   pOut->_43 = 0.0f; pOut->_44 = 1.0f;

    return pOut;
}

Zřetězení matic

Jednou z výhod použití matic je, že můžete kombinovat účinky dvou nebo více matic vynásobením. To znamená, že pokud chcete model otočit a pak ho přeložit na nějaké místo, nemusíte použít dvě matice. Místo toho vynásobíte rotační a translační matice, abyste vytvořili složenou matici, která obsahuje všechny jejich efekty. Tento proces, označovaný jako zřetězení matic, lze napsat pomocí následující rovnice.

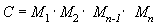
V této rovnici je C složená matice, která se vytváří, a M₁ až Mn jsou jednotlivé matice. Ve většině případů jsou zřetězeny pouze dvě nebo tři matice, ale neexistuje žádný limit.

Pořadí, ve kterém je násobení matice provedeno, je zásadní. Předchozí vzorec odráží pravidlo pro konkatenaci matic zleva doprava. To znamená, že viditelné efekty matic, které použijete k vytvoření složené matice, se objevují v pořadí zleva doprava. Typická světová matice je znázorněna v následujícím příkladu. Představte si, že vytváříte světovou matici pro stereotypní létající talíř. Pravděpodobně byste chtěli otočit létající talíř kolem jeho středu - osy y modelového prostoru - a přesunout ho na jiné místo ve vaší scéně. Abyste toho dosáhli, nejprve vytvoříte matici otočení a potom ji vynásobíte maticí překladu, jak je znázorněno v následující rovnici.

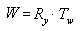
V tomto vzorci je R_y maticí pro otáčení osu y a T_w je překladem do určité pozice ve světových souřadnicích.

Pořadí, ve kterém násobíte matice, je důležité, protože na rozdíl od vynásobení dvou skalárních hodnot není násobení matice commutativní. Násobení matic v opačném pořadí má vizuální efekt překládání létajícího talíře na jeho světovou pozici vesmíru a následné otáčení po celém světě původu.

Bez ohledu na typ matice, kterou vytváříte, nezapomeňte pravidlo zleva doprava a ujistěte se, že dosáhnete očekávaných efektů.

související témata

Transformace