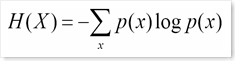Del via

Information Theory (1) - The Science of Communication

  • Artikel

IT is a beautiful sub-field of CS with applications across the gamut of scientific fields: coding theory and communications (under unreliable channels), cryptography, physics, biomedical engineering, computer graphics, machine learning, statistics, and even gambling and stock trading. It is truly a marvelous through process.

Framework:

  • "Bit" as the unit of communication. Arbitrary. Ok as long as all analysis is consistent.
  • Two parties: A and B. An event occurs at one end, A, who must "communicate" the outcome to B.
    • What are the minimum "units" required to communicate?
    • The Key insight from Shannon: it depends on apriori belief distribution about the event
    • That is, "uncertainty" with respect to the event. If an outcome is absolute or impossibly, why communicate at all?
  • For instance, a sequence of biased coin flips contains less information (less degree of uncertainty)  than a sequence of unbiased coin flips, so it should take fewer bits to transmit
  • Keep in mind that if the likelihood of n outcomes is not equally likely, we can use variable length encoding to use less bits to transmit more likely outcome.

Information Content / Degree of Uncertainty / "Entropy"

Entropy of R.V. X is denoted by H(X)

image

                = E[log( 1/p(X) )]

Intuition behind the formula:

  • Lets say all n events are equally likely and P(x) = p for all x.
    • Then, -log(p) = log(1/p), which is log(n).
  • But since the actual distribution may not be uniform, take the weighted average of information content of each possible outcome - weighted by the probability of the outcome occurring.
    • Thus, more frequent values can be encoded by smaller length messages.

 

Basic Results to Remember

  • Joint Entropy:  eq=H(X,Y) = \sum_{y \in Y} \sum_{x \in X} p(x,y) \; log \: p(x,y)

    • if X, Y are independent events, joint entropy is H(X) + H(Y)
    • Why? Need to communicate both, Duh!

  • Conditional Entropy:

    eq=H(Y|X) = \sum_{x \in X}^{} p(x) H(Y|X=x)

                   eq== - \sum_{x \in X} \sum_{y \in Y} p(x, y) \; log\; p(y|x)

    • How much extra information you still need to supply on avg to communicate Y, given that the outcome of X is known

  • Chain Rule:

    • H(X, Y) = H(X) + H(Y|X)   = H(Y) + H(X|Y)
    • H(X1 .., Xn) = .... just expand

  • Mutual Information:  I(X;Y) = H(X) - H(X|Y)

    • "Reduction" in uncertainty about one Random Variable by knowing the outcome of other
    • How far a joint distribution is from independence
    • The amount of information one R.V. contains about another
    • Note: I(X;X) = H(X) - H(X|X) = H(X)

  • Conditional Mutual Information and the chain rule

    •    I(X; (Y|Z))
    • = I( (X; Y)|Z)
    • = H(X|Z) - H(X|(Y, Z))

  • Kullback-Lieibler Divergence (Relative Entropy)

    • For two p.m.f. p(x) and q(x),
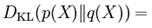
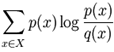
    • image  image
    • Measures how different two probability dists are over the same event space.
    • Avg number of bits that are wasted by encoding events from dist p with code based on dist q.
    • D(p||q)=0 iff p=q
    • Often seen as "distance" but not quite right because i) not symmetric in p an q, and ii) does not satisfy: d(x,y) <= d(x,z) + d(z, y)

  • Cross Entropy

    • Let p be the true dist, q be the model dist, then Cross entropy is defined as:
    • \mathrm{H}(p, q) = \mathrm{E}_p[-\log q] = \mathrm{H}(p) + D_{\mathrm{KL}}(p \| q)\!,
    • Avg number of bits needed to communicate events when coding scheme is based on model dist q rather than true dist p
    • Cross entropy minimization is typically used when a model dist q is to be designed (often without knowing true dist p)

 

Not so basic results and some applications of IT in Part 2 ..

Comments