Del via

Random Sampling over Joins

  • Artikel

Source: On Random Sampling over Joins. Surajit Chaudhuri, Rajeev Motwani, Vivek Narasayya, Sigmod 1999.

What?

  • Random sampling as a primitive relational operator: SAMPLE(R, f) where R is the relation and f the sample fraction.
  • SAMPLE(Q, f) is a tougher problem, where Q is a relation produced by a query
  • In particular, focus on sampling over a join operator
  • Can be generalize to arbitrarily deep join trees

Motivation:

  • Data mining scenarios - CUBE, OLAP, stream queries- need to sample a query rather than evaluate it
  • Statistical analysis when dealing with massive data
  • Massively distributed computing (information storage/retrieval) scenarios

Details:

  • Sampling Methods:
    1. With Replacement (WR),
    2. Without Replacement (WOR),
    3. Coin Flips (CF)
  • Conversion between methods is straightforward, as per my previous note.
  • Dimensions:
    • Sequential stream (critical for efficiently) vs random access on a materialized relation
    • Indexes, vs Stats vs no information
    • Weighted vs Unweighted sample
  • Note: Weighted, Sequential sample is the most general case

Sequential, unweighted: CF semantics - easy.
Sequential, unweighted, WOR - easy: Reservoir Sampling
Sequential, unweighted, WR - Algorithms:

Black Box U1: Relation R with n tuples, get WR sample of size r
Need to know the size of n :(
Produces samples while processing, preserves input order, O(n) time, O(1) extra memory

 x = r
i = 0
while(t = stream.Next())
{
    Generate random variable X from BinomialDist(x, 1/(n-i))
    result.Add( X copies of t)
    x = x - X
    i = i++
}

Black Box U2:

No need to know n . With some modification can preserve the order
Does not produce result till the end.  O(n) time, O(r) space

 N=0
Result[1..r]
while(t = stream.Next())
{
   N++
   for(j = 1 to r)
   {
       if(Rand.New(0,1) < 1/N)
           Result[j] = t
   }
}
return Result
Weighted Sampling

The above two algorithms can be easily modified for the weighted case:

Weighted U1

 x = r, i = 0
W = sum of w(t), the weights for each input tuple t
while(t = stream.Next() && x>0)
{
    Generate random variable X from BinomialDist(x, w(t)/(W-i))
    result.Add( X copies of t)
    x = x - X
    i = i+ w(t)
}

Weighted U2

 W=0
Result[1..r]
while(t = stream.Next())
{
   W = W + w(t)
   for(j = 1 to r)
   {
       if(Rand.New(0,1) < w(t)/W)
           Result[j] = t
   }
}
return Result
The difficulty in Join Sampling

Example: R1 = {1, 2, ..., 1000}, R2 = {1, 1, 1, ..... 1}. Unlikely that R1(1) will be sampled, and SAMPLE(R1) 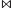image SAMPLE(R2) will contain no result

  • SAMPLE does not commute with join
  • Sample tuple t from R1 with probability proportional to |R2(t)|

Algorithms

Let m1(v) denote the number of tuples in R1 that contain value v in the attribute to be used in equi-join.

Strategy Naive Sampling: produces WR samples

Compute J = R1 image R2
Use U1 or U2 to produce SAMPLE(J)

Strategy Olken Sample: produces WR samples
Requires indexes for R1 and R2

Let M be upper bound on m2(v) for all values A can take, which is essentially all rows in R2 (?)

while r tuples have not been produced
{
     Randomly pick a tuple t1 from R1 
     Randomly pick a tuple t2 from imageA=t1.A ( R2 )
     With probability  m2(t2.A)/M, output t1 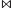image t2
}

Strategy Stream Sample   [Chaudhury, Motwani, Narasayya]
No information for R1, R2 has indexes/stats.

  1. Use a with-replacement strategy and get a sample WR (S1) from R1 WHERE tuple t (from R1) has weight m2(t.A)
  2. while(t1 = S1.next())
    {
        t2 = random sample from (SELECT t from R2 where t.A = t1.A)
        output t1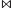 image t2
    }
  • 'non-oblivious sampling', where the distribution of R2 is used to bias the sample from R1
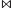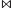  • What about R1 image R2 image R3?
    • Pick non-uniform random sample for R1 image R2  whose distribution depends on R3
    • Sample from R1 using stats for R2 and R3.
  • Using the same biasing idea to push down both operand relations
    • Cross-dependent sampling strategy difficult

Other Results:

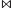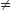  • Not possible to commute SAMPLE over JOIN. That is, SAMPLE(R1 image R3) image SAMPLE(R1) 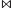image SAMPLE(R2)
  • Can push down SAMPLE to one side of JOIN tree by biasing the sample with respect to the other side of JOIN.

Comments