Regression

Fuldført

Notat

Se fanen Tekst og billeder for flere detaljer!

Regressionsmodeller trænes til at forudsige numeriske mærkatværdier baseret på træningsdata, der indeholder både funktioner og kendte mærkater. Processen til træning af en regressionsmodel (eller faktisk enhver overvåget maskinlæringsmodel) involverer flere iterationer, hvor du bruger en passende algoritme (normalt med nogle parameteriserede indstillinger) til at træne en model, evaluere modellens forudsigende ydeevne og forfine modellen ved at gentage træningsprocessen med forskellige algoritmer og parametre, indtil du opnår et acceptabelt niveau af forudsigende nøjagtighed.

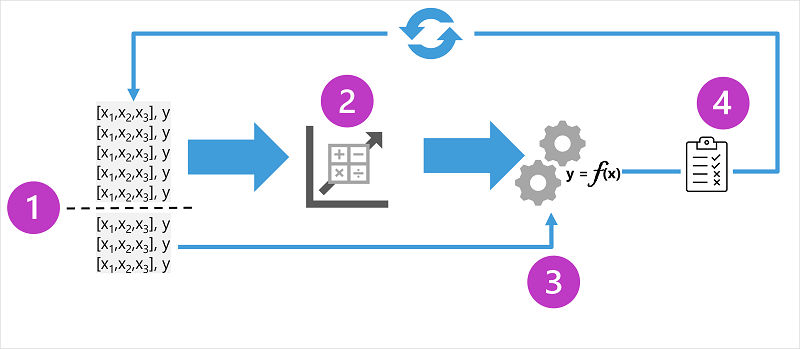
Diagrammet viser fire nøgleelementer i oplæringsprocessen for overvågede modeller til maskinel indlæring:

1. Opdel træningsdataene (tilfældigt) for at oprette et datasæt, som modellen skal trænes med, mens du holder et undersæt af de data, du vil bruge til at validere den trænede model, tilbage.
2. Brug en algoritme til at tilpasse træningsdataene til en model. I tilfælde af en regressionsmodel skal du bruge en regressionsalgoritme såsom lineær regression.
3. Brug de valideringsdata, du har tilbageholdt, til at teste modellen ved at forudsige mærkater for funktionerne.
4. Sammenlign de kendte faktiske mærkater i valideringsdatasættet med de mærkater, som modellen forudsagde. Aggregerer derefter forskellene mellem de forudsagte og faktiske etiketværdier for at beregne en metrikværdi, der angiver, hvor nøjagtigt modellen forudsagde for valideringsdataene.

Efter hver træning, validering og evaluering af gentagelse kan du gentage processen med forskellige algoritmer og parametre, indtil der opnås en acceptabel evalueringsmetrikværdi.

Eksempel - regression

Lad os undersøge regression med et forenklet eksempel, hvor vi træner en model til at forudsige en numerisk etiket (y) baseret på en enkelt funktionsværdi (x). De fleste virkelige scenarier involverer flere funktionsværdier, hvilket tilføjer en vis kompleksitet; men princippet er det samme.

Lad os for eksempel holde os til det issalgsscenarie, vi diskuterede tidligere. Til vores funktion vil vi overveje temperaturen (lad os antage, at værdien er den maksimale temperatur på en given dag), og den etiket, vi vil træne en model til at forudsige, er antallet af is, der sælges den dag. Vi starter med nogle historiske data, der inkluderer optegnelser over daglige temperaturer (x) og issalg (y):

Temperatur (x)	Salg af is (y)
51	1
52	0
67	14
65	14
70	23
69	20
72	23
75	26
73	22
81	30
78	26
83	36

Træning af en regressionsmodel

Vi starter med at opdele dataene og bruge en delmængde af dem til at træne en model. Her er træningsdatasættet:

Temperatur (x)	Salg af is (y)
51	1
65	14
69	20
72	23
75	26
81	30

For at få et indblik i, hvordan disse x- og y-værdier kan relatere til hinanden, kan vi plotte dem som koordinater langs to akser, sådan her:

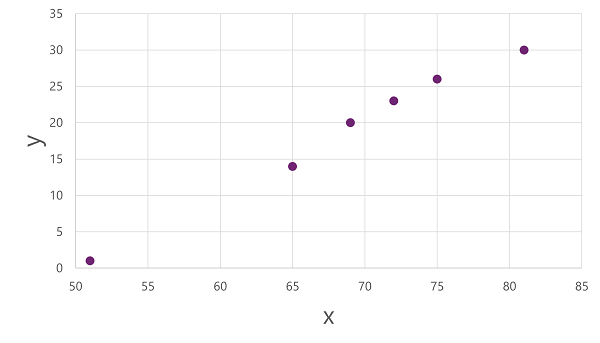
Nu er vi klar til at anvende en algoritme på vores træningsdata og tilpasse den til en funktion, der anvender en operation på x for at beregne y. En sådan algoritme er lineær regression, som fungerer ved at udlede en funktion, der producerer en lige linje gennem skæringspunkterne mellem x - og y-værdierne , samtidig med at den gennemsnitlige afstand mellem linjen og de plottede punkter minimeres, som denne:

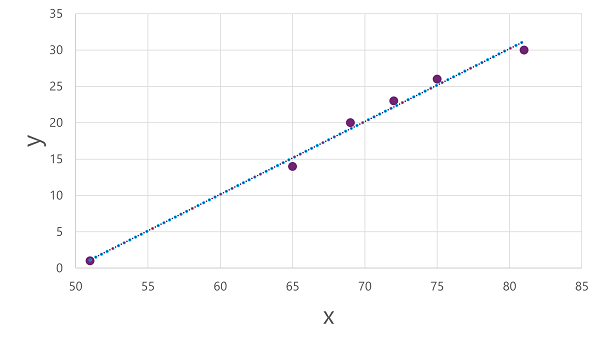
Linjen er en visuel repræsentation af den funktion, hvor linjens hældning beskriver, hvordan man beregner værdien af y for en given værdi af x. Linjen opfanger x-aksen ved 50, så når x er 50, er y 0. Som du kan se fra aksemarkørerne i plottet, hælder linjen, så hver stigning på 5 langs x-aksen resulterer i en stigning på 5 op ad y-aksen ; så når x er 55, er y 5; Når x er 60, er y 10 og så videre. For at beregne en værdi af y for en given værdi af x, trækker funktionen simpelthen 50 fra; Med andre ord kan funktionen udtrykkes således:

f(x) = x-50

Du kan bruge denne funktion til at forudsige antallet af is, der sælges på en dag med en given temperatur. Antag for eksempel, at vejrudsigten fortæller os, at det i morgen bliver 77 grader. Vi kan anvende vores model til at beregne 77-50 og forudsige, at vi sælger 27 is i morgen.

Men hvor nøjagtig er vores model?

Evaluering af en regressionsmodel

For at validere modellen og evaluere, hvor godt den forudsiger, holdt vi nogle data tilbage, som vi kender etiketten (y) værdi for. Her er de data, vi holdt tilbage:

Temperatur (x)	Salg af is (y)
52	0
67	14
70	23
73	22
78	26
83	36

Vi kan bruge modellen til at forudsige etiketten for hver af observationerne i dette datasæt baseret på funktionsværdien (x); og derefter sammenligne den forudsagte etiket (ŷ) med den kendte faktiske etiketværdi (y).

Ved at bruge den model, vi trænede tidligere, som indkapsler funktionen f(x) = x-50, resulterer det i følgende forudsigelser:

Temperatur (x)	Faktisk salg (y)	Forventet salg (ŷ)
52	0	2
67	14	17
70	23	20
73	22	23
78	26	28
83	36	33

Vi kan plotte både de forudsagte og faktiske etiketter i forhold til funktionsværdierne på denne måde:

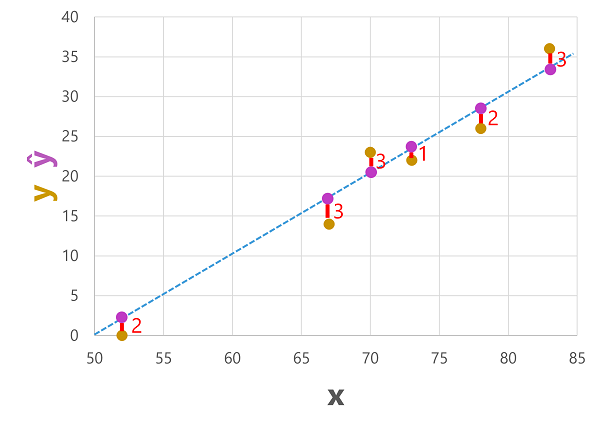
De forudsagte etiketter beregnes af modellen, så de er på funktionslinjen, men der er en vis afvigelse mellem de ŷ-værdier , der beregnes af funktionen, og de faktiske y-værdier fra valideringsdatasættet. som er angivet på plottet som en linje mellem ŷ - og y-værdierne , der viser, hvor langt fra forudsigelsen var fra den faktiske værdi.

Målepunkter for regressionsevaluering

Baseret på forskellene mellem de forudsagte og faktiske værdier kan du beregne nogle almindelige målepunkter, der bruges til at evaluere en regressionsmodel.

Gennemsnitlig absolut fejl (MAE)

Variansen i dette eksempel angiver, hvor mange is hver forudsigelse var forkert. Det er ligegyldigt, om forudsigelsen var over eller under den faktiske værdi (så f.eks. angiver -3 og +3 begge en varians på 3). Denne metrik er kendt som den absolutte fejl for hver forudsigelse og kan opsummeres for hele valideringssættet som den gennemsnitlige absolutte fejl (MAE).

I iseksemplet er gennemsnittet (gennemsnittet) af de absolutte fejl (2, 3, 3, 1, 2 og 3) 2,33.

Middelværdi kvadreret fejl (MSE)

Den gennemsnitlige absolutte fejlmetrik tager højde for alle uoverensstemmelser mellem forudsagte og faktiske etiketter i lige høj grad. Det kan dog være mere ønskeligt at have en model, der konsekvent er forkert med en lille mængde end en, der laver færre, men større fejl. En måde at producere en metrik, der "forstærker" større fejl ved at kvadrere de enkelte fejl og beregne gennemsnittet af de kvadrerede værdier. Denne metrik er kendt som den gennemsnitlige kvadratfejl (MSE).

I vores iseksempel er gennemsnittet af de kvadrerede absolutte værdier (som er 4, 9, 9, 1, 4 og 9) 6.

Root Mean Squared Error (RMSE)

Den gennemsnitlige kvadrerede fejl hjælper med at tage højde for størrelsen af fejl, men fordi den kvadrerer fejlværdierne, repræsenterer den resulterende metrik ikke længere den mængde, der måles af etiketten. Med andre ord kan vi sige, at MSE i vores model er 6, men det måler ikke dens nøjagtighed i form af antallet af is, der blev fejlforudsiget; 6 er blot en numerisk score, der angiver fejlniveauet i valideringsforudsigelserne.

Hvis vi vil måle fejlen i forhold til antallet af is, skal vi beregne kvadratroden af MSE; som producerer en metrik kaldet, ikke overraskende, Root Mean Squared Error. I dette tilfælde √6, hvilket er 2,45 (is).

Bestemmelseskoefficient (R²)

Alle målinger indtil videre sammenligner uoverensstemmelsen mellem de forudsagte og faktiske værdier for at evaluere modellen. Men i virkeligheden er der en naturlig tilfældig varians i det daglige salg af is, som modellen tager højde for. I en lineær regressionsmodel passer træningsalgoritmen til en lige linje, der minimerer den gennemsnitlige varians mellem funktionen og de kendte etiketværdier. Bestemmelseskoefficienten (mere almindeligt omtalt som R² eller R-kvadrat) er en metrik, der måler andelen af varians i valideringsresultaterne, der kan forklares af modellen, i modsætning til et unormalt aspekt af valideringsdataene (for eksempel en dag med et meget usædvanligt antal issalg på grund af en lokal festival).

Beregningen for R² er mere kompleks end for de tidligere målinger. Den sammenligner summen af kvadrerede forskelle mellem forudsagte og faktiske etiketter med summen af kvadrerede forskelle mellem de faktiske etiketværdier og gennemsnittet af faktiske etiketværdier, sådan her:

R² = 1- ∑(y-ŷ)² ÷ ∑(y-ȳ)²

Du skal ikke bekymre dig for meget, hvis det ser kompliceret ud; De fleste værktøjer til maskinel indlæring kan beregne metrikken for dig. Det vigtige er, at resultatet er en værdi mellem 0 og 1, der beskriver den andel af variansen, som modellen forklarer. Enkelt sagt, jo tættere på 1 denne værdi er, jo bedre passer modellen til valideringsdataene. I tilfælde af isregressionsmodellen er R² beregnet ud fra valideringsdataene 0,95.

Iterativ træning

De målepunkter, der er beskrevet ovenfor, bruges ofte til at evaluere en regressionsmodel. I de fleste scenarier i den virkelige verden vil en dataforsker bruge en iterativ proces til gentagne gange at træne og evaluere en model, varierende:

• Valg og forberedelse af funktioner (valg af, hvilke funktioner der skal medtages i modellen, og beregninger anvendt på dem for at sikre en bedre tilpasning).
• Algoritmevalg (Vi undersøgte lineær regression i det foregående eksempel, men der er mange andre regressionsalgoritmer)
• Algoritmeparametre (numeriske indstillinger til at styre algoritmens adfærd, mere præcist kaldet hyperparametre for at skelne dem fra x - og y-parametrene ).

Efter flere gentagelser vælges den model, der resulterer i den bedste evalueringsmetrikværdi, der er acceptabel for det specifikke scenarie.