Dyb læring

Fuldført

Seddel

Se fanen Tekst og billeder for flere detaljer!

Dyb læring er en avanceret form for maskinel indlæring, der forsøger at emulere den måde, den menneskelige hjerne lærer på. Nøglen til dyb læring er oprettelsen af et kunstigt neuralt netværk , der simulerer elektrokemisk aktivitet i biologiske neuroner ved hjælp af matematiske funktioner, som vist her.

Biologisk neuralt netværk	Kunstigt neuralt netværk
Neuroner brand som reaktion på elektrokemiske stimuli. Når signalet udløses, sendes signalet til forbundne neuroner.	Hver neuron er en funktion, der opererer på en inputværdi (x) og en vægt (w). Funktionen er ombrudt i en aktiveringsfunktion , der bestemmer, om outputtet skal overføres.

Kunstige neurale netværk består af flere lag af neuroner – der i bund og grund definerer en dybt indlejret funktion. Denne arkitektur er årsagen til, at teknikken kaldes dyb læring , og de modeller, der produceres af den, kaldes ofte dybe neurale netværk (DNN'er). Du kan bruge dybe neurale netværk til mange typer problemer med maskinel indlæring, herunder regression og klassificering samt mere specialiserede modeller til behandling af naturligt sprog og computersyn.

På samme måde som med andre teknikker til maskinel indlæring, der beskrives i dette modul, omfatter dyb læring tilpasning af oplæringsdata til en funktion, der kan forudsige en mærkat (y) baseret på værdien af en eller flere funktioner (x). Funktionen (f(x)) er det ydre lag af en indlejret funktion, hvor hvert lag af det neurale netværk indkapsler funktioner, der fungerer på x og de vægtværdier (w), der er knyttet til dem. Den algoritme, der bruges til at oplære modellen, omfatter iterativt at fodre funktionsværdierne (x) i oplæringsdataene frem gennem lagene for at beregne outputværdier for ŷ og validere modellen for at evaluere, hvor langt fra de beregnede ŷ værdier er fra de kendte y-værdier (hvilket kvantificerer fejlniveauet eller tabet i modellen) og derefter ændre vægt (w) for at reducere tabet. Den oplærte model indeholder de endelige vægtværdier, der resulterer i de mest nøjagtige forudsigelser.

Eksempel – Brug af deep learning til klassificering

Lad os udforske et eksempel, hvor et neuralt netværk bruges til at definere en klassificeringsmodel for pingvinarter, for bedre at forstå, hvordan en dyb neural netværksmodel fungerer.

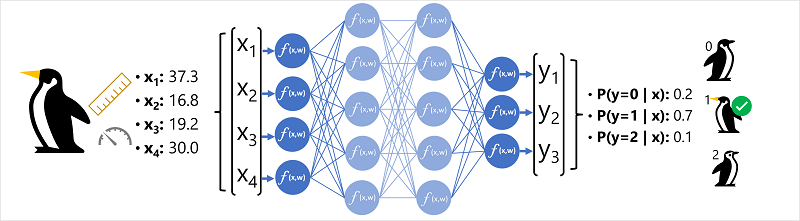
Funktionsdataene (x) består af nogle målinger af en pingvin. Målingerne er specifikt:

• Længden af pingvinens regning.
• Dybden af pingvinens regning.
• Længden af pingvinens svømmefødder.
• Pingvinens vægt.

I dette tilfælde er x en vektor med fire værdier eller matematisk x =[x1,x2,x3,x4].

Den etiket, vi forsøger at forudsige (y) er arten af pingvinen, og at der er tre mulige arter, det kunne være:

• Adelie
• Gentoo
• Chinstrap

Dette er et eksempel på et klassificeringsproblem, hvor modellen til maskinel indlæring skal forudsige den mest sandsynlige klasse, som en observation tilhører. En klassificeringsmodel opnår dette ved at forudsige en etiket, der består af sandsynligheden for hver klasse. Med andre ord er y en vektor med tre sandsynlighedsværdier. én for hver af de mulige klasser: [P(y=0|x), P(y=1|x), P(y=2|x)].

Processen til at udlede en forudsagt pingvinklasse ved hjælp af dette netværk er:

1. Funktionsvektoren for en pingvinobservation føres ind i inputlaget i det neurale netværk, som består af en neuron for hver x-værdi . I dette eksempel bruges følgende x-vektor som input: [37.3, 16.8, 19.2, 30.0]
2. Funktionerne for det første lag af neuroner beregner hver en vægtet sum ved at kombinere x-værdien og w-vægten og overføre den til en aktiveringsfunktion, der bestemmer, om den opfylder den tærskel, der skal overføres til det næste lag.
3. Hver neuron i et lag er forbundet til alle neuronerne i det næste lag (en arkitektur kaldes også et fuldt forbundet netværk), så resultaterne af hvert lag føres fremad gennem netværket, indtil de når outputlaget.
4. Outputlaget producerer en vektor af værdier. i dette tilfælde ved hjælp af et softmax eller lignende funktion til at beregne sandsynlighedsfordelingen for de tre mulige klasser af pingvin. I dette eksempel er outputvektoren: [0.2, 0.7, 0.1]
5. Vektorens elementer repræsenterer sandsynlighederne for klasserne 0, 1 og 2. Den anden værdi er den højeste, så modellen forudsiger, at pingvinarten er 1 (Gentoo).

Hvordan lærer et neuralt netværk det?

Vægtene i et neuralt netværk er centrale for, hvordan det beregner forudsagte værdier for mærkater. Under oplæringsprocessen lærer modellen de vægte, der vil resultere i de mest nøjagtige forudsigelser. Lad os udforske træningsprocessen lidt mere detaljeret for at forstå, hvordan denne læring finder sted.

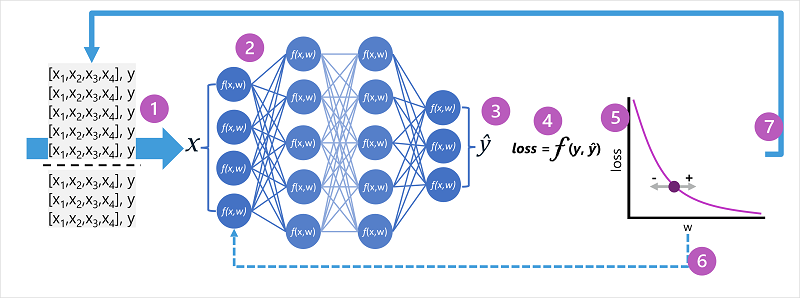
1. Oplærings- og valideringsdatasættene er defineret, og oplæringsfunktionerne føres ind i inputlaget.
2. Neuronerne i hvert lag af netværket anvender deres vægte (som oprindeligt tildeles tilfældigt) og fodrer dataene gennem netværket.
3. Outputlaget producerer en vektor, der indeholder de beregnede værdier for ŷ. Et output til en forudsigelse af pingvinklassen kan f.eks. være [0.3. 0.1. 0.6].
4. En tabsfunktion bruges til at sammenligne de forudsagte ŷ-værdier med de kendte y-værdier og aggregere forskellen (som kaldes tabet). Hvis den kendte klasse for det tilfælde, der returnerede outputtet i det forrige trin, f.eks. er Chinstrap, skal y-værdien være [0.0, 0.0, 1.0]. Den absolutte forskel mellem dette og vektoren ŷ er [0.3, 0.1, 0.4]. I virkeligheden beregner tabsfunktionen den samlede varians for flere sager og opsummerer den som en enkelt tabsværdi .
5. Da hele netværket i bund og grund er en stor indlejret funktion, kan en optimeringsfunktion bruge differentialkalkulus til at evaluere hver vægts indflydelse på tabet og bestemme, hvordan de kan justeres (op eller ned) for at reducere mængden af samlet tab. Den specifikke optimeringsteknik kan variere, men involverer normalt en gradueringsstigning , hvor hver vægt øges eller reduceres for at minimere tabet.
6. Ændringerne i vægterne er overført til lagene i netværket og erstatter de tidligere anvendte værdier.
7. Processen gentages over flere gentagelser (kendt som epoker), indtil tabet minimeres, og modellen forudsiger acceptabelt nøjagtigt.

Seddel

Selvom det er nemmere at tænke på hvert enkelt tilfælde i de oplæringsdata, der overføres via netværket én ad gangen, er dataene i virkeligheden samlet i matrixer og behandlet ved hjælp af lineære algebraiske beregninger. Derfor udføres træning af neurale netværk bedst på computere med grafiske behandlingsenheder (GPU'er), der er optimeret til vektor- og matrixmanipulation.