Semantiske sprogmodeller

  • 4 minutter

Notat

Se fanen Tekst og billeder for flere detaljer!

Som det nyeste inden for NLP er avanceret, har evnen til at oplære modeller, der indkapsler det semantiske forhold mellem tokens, ført til fremkomsten af effektive modeller til deep learning language. Kernen i disse modeller er kodningen af sprogtokens som vektorer (matrixer med flere værdier), der kaldes integreringer.

Denne vektorbaserede tilgang til modellering af tekst blev almindelig med teknikker som Word2Vec og GloVe, hvor teksttokens repræsenteres som tætte vektorer med flere dimensioner. Under modeltræning tildeles dimensionsværdierne for at afspejle de semantiske karakteristika for hvert token baseret på deres anvendelse i træningsteksten. De matematiske relationer mellem vektorerne kan derefter udnyttes til at udføre almindelige tekstanalyseopgaver mere effektivt end ældre rent statistiske teknikker. En nyere fremgang i denne tilgang er at bruge en teknik kaldet opmærksomhed til at betragte hvert token i kontekst og beregne indflydelsen af tokens omkring det. De resulterende kontekstualiserede embeddings, som dem der findes i GPT-familien af modeller, danner grundlaget for moderne generativ AI.

Fremstilling af tekst som vektorer

Vektorer repræsenterer punkter i flerdimensionelt rum, defineret af koordinater langs flere akser. Hver vektor beskriver en retning og afstand fra origo. Semantisk lignende tokens bør resultere i vektorer, der har en lignende orientering – med andre ord peger de i lignende retninger.

For eksempel, overvej følgende tredimensionelle indlejringer for nogle almindelige ord:

Ord Vektor
dog [0.8, 0.6, 0.1]
puppy [0.9, 0.7, 0.4]
cat [0.7, 0.5, 0.2]
kitten [0.8, 0.6, 0.5]
young [0.1, 0.1, 0.3]
ball [0.3, 0.9, 0.1]
tree [0.2, 0.1, 0.9]

Vi kan visualisere disse vektorer i tredimensionelt rum som vist her:

Diagram over en 3D-visualisering af ordvektorer.

Vektorerne for "dog" og "cat" er ens (begge husdyr), ligesom "puppy" og "kitten" (begge unge dyr). Ordene "tree", "young", og ball" har tydeligt forskellige vektororienteringer, hvilket afspejler deres forskellige semantiske betydninger.

Den semantiske karakteristik kodet i vektorerne gør det muligt at bruge vektorbaserede operationer, der sammenligner ord og muliggør analytiske sammenligninger.

Da vektorernes orientering bestemmes af deres dimensionsværdier, har ord med lignende semantiske betydninger tendens til at have lignende orienteringer. Det betyder, at du kan bruge beregninger som cosinuslighed mellem vektorer til at lave meningsfulde sammenligninger.

For eksempel, for at bestemme "den mærkelige én" mellem "dog", "cat", og "tree", kan du beregne cosinusligheden mellem par af vektorer. Cosinusligheden beregnes som:

cosine_similarity(A, B) = (A · B) / (||A|| * ||B||)

Hvor A · B er prikproduktet og ||A|| er størrelsen af vektor A.

Beregning af ligheder mellem de tre ord:

  • dog [0,8, 0,6, 0,1] og cat [0,7, 0,5, 0,2]:

    • Punktprodukt: (0,8 × 0,7) + (0,6 × 0,5) + (0,1 × 0,2) = 0,56 + 0,30 + 0,02 = 0,88
    • Størrelse af dog: √(0,8² + 0,6² + 0,1²) = √(0,64 + 0,36 + 0,01) = √1,01 ≈ 1,005
    • Størrelse af cat: √(0,7² + 0,5² + 0,2²) = √(0,49 + 0,25 + 0,04) = √0,78 ≈ 0,883
    • Cosinus-lighed: 0,88 / (1,005 × 0,883) ≈ 0,992 (høj lighed)

  • dog [0,8, 0,6, 0,1] og tree [0,2, 0,1, 0,9]:

    • Punktprodukt: (0,8 × 0,2) + (0,6 × 0,1) + (0,1 × 0,9) = 0,16 + 0,06 + 0,09 = 0,31
    • Magnitude af tree: √(0,2² + 0,1² + 0,9²) = √(0,04 + 0,01 + 0,81) = √0,86 ≈ 0,927
    • Cosinuslighed: 0,31 / (1,005 × 0,927) ≈ 0,333 (lav lighed)

  • cat [0,7, 0,5, 0,2] og tree [0,2, 0,1, 0,9]:

    • Punktprodukt: (0,7 × 0,2) + (0,5 × 0,1) + (0,2 × 0,9) = 0,14 + 0,05 + 0,18 = 0,37
    • Cosinuslighed: 0,37 / (0,883 × 0,927) ≈ 0,452 (lav lighed)

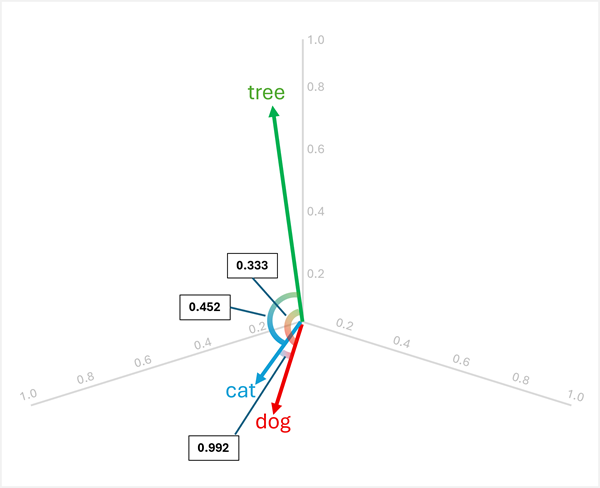
Diagram over cosinus-lighedsvisualisering, der viser hunde-, katte- og trævektorer.

Resultaterne viser, at "dog" og "cat" er meget ens (0,992), mens "tree" har lavere lighed med både "dog" (0,333) og "cat" (0,452). Derfor er han tree tydeligvis den mærkelige.

Vektortranslation gennem addition og subtraktion

Du kan tilføje eller trække vektorer fra for at få nye vektorbaserede resultater; som derefter kan bruges til at finde tokens med matchende vektorer. Denne teknik muliggør intuitiv aritmetikbaseret logik til at bestemme passende termer baseret på sproglige relationer.

For eksempel, ved at bruge vektorerne fra tidligere:

  • dog + young = [0,8, 0,6, 0,1] + [0,1, 0,1, 0,3] = [0,9, 0,7, 0,4] = puppy
  • cat + young = [0,7, 0,5, 0,2] + [0,1, 0,1, 0,3] = [0,8, 0,6, 0,5] = kitten

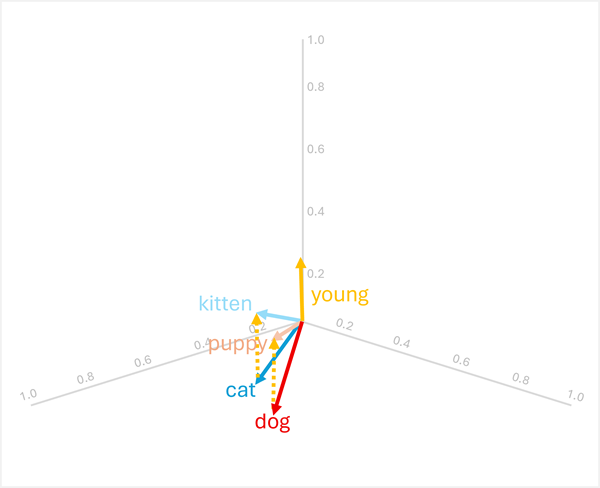
Diagram over vektoraddition, der viser hund + unge = hvalp og kat + unge = killing.

Disse operationer virker, fordi vektoren for "young" koder den semantiske transformation fra et voksent dyr til dets unge modstykke.

Notat

I praksis producerer vektoraritmetik sjældent eksakte match; I stedet ville du søge efter det ord, hvis vektor er tættest (mest lignende) resultatet.

Aritmetikken fungerer også omvendt:

  • puppy - young = [0,9, 0,7, 0,4] - [0,1, 0,1, 0,3] = [0,8, 0,6, 0,1] = dog
  • kitten - young = [0,8, 0,6, 0,5] - [0,1, 0,1, 0,3] = [0,7, 0,5, 0,2] = cat

Analogisk ræsonnement

Vektoraritmetik kan også besvare analogispørgsmål som "puppy er til som dogkitten er til ?"

For at løse dette, beregn: kitten - puppy + dog

  • [0.8, 0.6, 0.5] - [0.9, 0.7, 0.4] + [0.8, 0.6, 0.1]
  • = [-0,1, -0,1, 0,1] + [0,8, 0,6, 0,1]
  • = [0.7, 0.5, 0.2]
  • = cat

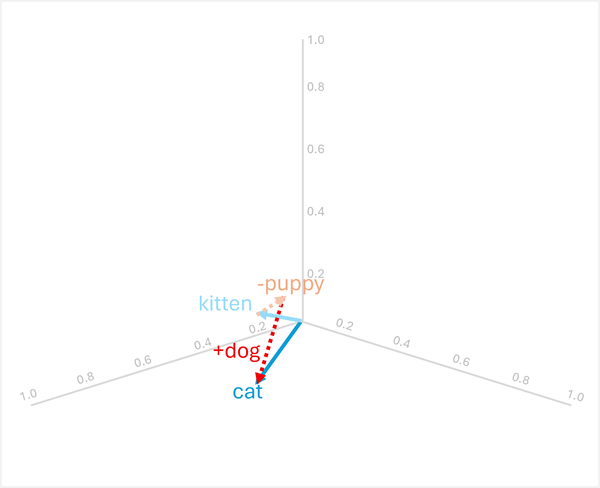
Diagram over vektoraritmetik, der viser killing - hvalp + hund = kat.

Disse eksempler demonstrerer, hvordan vektoroperationer kan fange sproglige relationer og muliggøre ræsonnement om semantiske mønstre.

Brug af semantiske modeller til tekstanalyse

Vektorbaserede semantiske modeller giver kraftfulde funktioner til mange almindelige tekstanalyseopgaver.

Tekstresumé

Semantiske indlejringer muliggør ekstraktiv opsummering ved at identificere sætninger med vektorer, der er mest repræsentative for det samlede dokument. Ved at kode hver sætning som en vektor (ofte ved at gennemsnitliggøre eller samle indlejringerne af dens bestanddele) kan du beregne, hvilke sætninger der er mest centrale for dokumentets betydning. Disse centrale sætninger kan udtrækkes for at danne et resumé, der indfanger de centrale temaer.

Nøgleordsudtrækning

Vektorlighed kan identificere de vigtigste termer i et dokument ved at sammenligne hvert ords indlejring med dokumentets overordnede semantiske repræsentation. Ord, hvis vektorer ligner dokumentets vektor mest, eller som er mest centrale, når man tager alle ordvektorer i dokumentet i betragtning, er sandsynligvis nøgletermer, der repræsenterer hovedemnerne.

Genkendelse af navngivne enheder

Semantiske modeller kan finjusteres til at genkende navngivne enheder (personer, organisationer, lokationer osv.) ved at lære vektorrepræsentationer, der samler lignende entitetstyper sammen. Under inferensen undersøger modellen hver tokens embedding og dens kontekst for at afgøre, om den repræsenterer en navngiven enhed, og i så fald hvilken type.

Tekstklassifikation

For opgaver som sentimentanalyse eller emnekategorisering kan dokumenter repræsenteres som aggregerede vektorer (såsom gennemsnittet af alle ordindlejringer i dokumentet). Disse dokumentvektorer kan derefter bruges som funktioner til maskinlæringsklassifikatorer eller sammenlignes direkte med klasseprototypevektorer for at tildele kategorier. Fordi semantisk lignende dokumenter har lignende vektororienteringer, grupperer denne tilgang effektivt relateret indhold og skelner mellem forskellige kategorier.