Hvad er klassificering?
binær klassificering er klassificering med to kategorier. Vi kan f.eks. mærke patienter som ikke-diabetiker eller diabetiker.
Klasseforudsigelsen foretages ved at bestemme sandsynlighed for hver mulige klasse som en værdi mellem 0 (umulig) og 1 (sikker). Den samlede sandsynlighed for alle klasser er altid 1, da patienten er absolut enten diabetiker eller ikke-diabetiker. Så hvis den forudsagte sandsynlighed for, at en patient er diabetiker, er 0,3, er der en tilsvarende sandsynlighed på 0,7, at patienten ikke er diabetiker.
En grænseværdi, ofte 0,5, bruges til at bestemme den forudsagte klasse. Hvis positiv klasse (i dette tilfælde diabetiker) har en forudsagt sandsynlighed, der er større end tærsklen, forudsiges en klassificering af diabetiker.
Oplæring og evaluering af en klassificeringsmodel
Klassificering er et eksempel på en overvåget maskinel indlæringsteknik, hvilket betyder, at den er afhængig af data, der omfatter kendte funktionsværdier værdier og kendte mærkat værdier. I dette eksempel er funktionsværdierne diagnosticeringsmålinger for patienter, og mærkatværdierne er en klassificering af ikke-diabetes eller diabetiker. En klassificeringsalgoritme bruges til at tilpasse et undersæt af dataene til en funktion, der kan beregne sandsynligheden for hver klassemærkat ud fra funktionsværdierne. De resterende data bruges til at evaluere modellen ved at sammenligne de forudsigelser, den genererer fra funktionerne, med de kendte klassemærkater.
Et simpelt eksempel
Lad os udforske et eksempel for at forklare de vigtigste principper. Lad os antage, at vi har følgende patientdata, som består af en enkelt funktion (blodglukoseniveau) og en klassemærkat 0 for ikke-diabetiker, 1 for diabetiker.
| Blood-Glucose | Diabetiker |
|---|---|
| 82 | 0 |
| 92 | 0 |
| 112 | 1 |
| 102 | 0 |
| 115 | 1 |
| 107 | 1 |
| 87 | 0 |
| 120 | 1 |
| 83 | 0 |
| 119 | 1 |
| 104 | 1 |
| 105 | 0 |
| 86 | 0 |
| 109 | 1 |
Vi bruger de første otte observationer til at oplære en klassificeringsmodel, og vi starter med at afbilde blodglukosefunktionen (x) og den forudsagte diabetiske etiket (y).
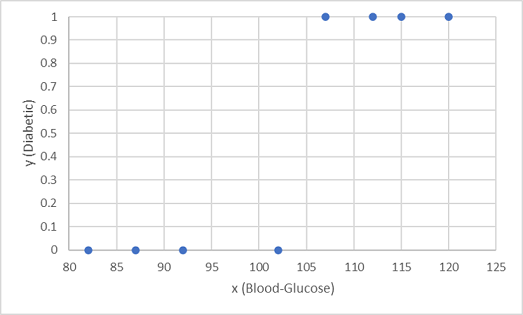
Det, vi har brug for, er en funktion, der beregner en sandsynlighedsværdi for y- baseret på x (med andre ord skal vi bruge funktionen f(x) = y). Du kan se fra diagrammet, at patienter med et lavt blodsukkerniveau alle ikke er diabetiker, mens patienter med et højere blodglukoseniveau er diabetiker. Jo højere glukoseniveauet er, jo mere sandsynligt er det, at en patient er diabetiker, hvor bøjningspunktet er et sted mellem 100 og 110. Vi skal tilpasse en funktion, der beregner en værdi mellem 0 og 1 for y til disse værdier.
En sådan funktion er en logistisk funktion, som danner en sigmoidal (S-formet) kurve.
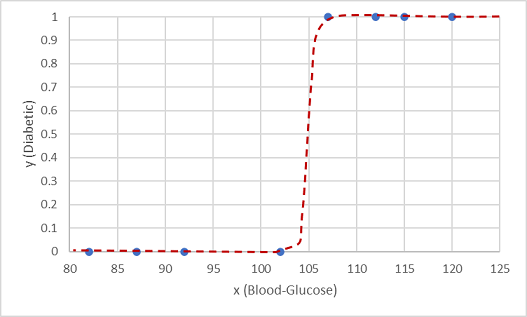
Nu kan vi bruge funktionen til at beregne en sandsynlighedsværdi, der y er positiv, hvilket betyder, at patienten er diabetiker fra en hvilken som helst værdi af x ved at finde punktet på funktionslinjen for x. Vi kan angive en grænseværdi på 0,5 som afskæringspunkt for forudsigelsen af klassemærkaten.
Lad os teste den med de to dataværdier, vi holdt tilbage.
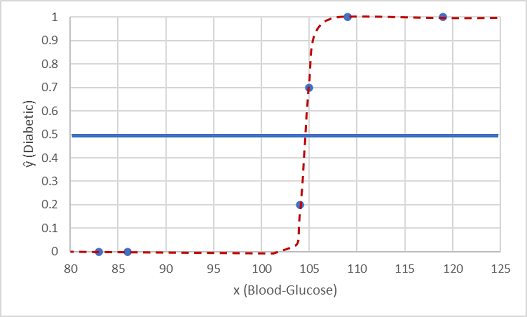
Punkter, der afbildes under tærskellinjen, giver en forudsagt klasse på 0 (ikke-diabetiker), og punkter over linjen forudsiges som 1 (diabetiker).
Nu kan vi sammenligne mærkatforudsigelserne (ŷeller "y-hat" baseret på den logistiske funktion, der er indkapslet i modellen, med de faktiske klassemærkater (y).
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |