Note
Access to this page requires authorization. You can try signing in or changing directories.
Access to this page requires authorization. You can try changing directories.
In this article you'll find a detailed theoretical explanation of the mathematical principles that make Grover's algorithm work.
For a practical implementation of Grover's algorithm to solve mathematical problems, see Implement Grover's search algorithm.
Statement of the problem
Grover's algorithm speeds up the solution to unstructured data searches (or search problem), running the search in fewer steps than any classical algorithm could. Any search task can be expressed with an abstract function $f(x)$ that accepts search items $x$. If the item $x$ is a solution to the search task, then $f(x)=1$. If the item $x$ isn't a solution, then $f(x)=0$. The search problem consists of finding any item $x_0$ such that $f(x_0)=1$.
Any problem that allows you to check whether a given value $x$ is a valid solution (a "yes or no problem") can be formulated in terms of the search problem. The following are some examples:
- Boolean satisfiability problem: Given a set of Boolean values, does the set satisfy a given Boolean formula?
- Traveling salesman problem: What is the shortest possible loop that connects all cities?
- Database search problem: Does a database table contain the record $x$?
- Integer factorization problem: Is the number $N$ divisible by the number $x$?
The task that Grover's algorithm aims to solve can be expressed as follows: given a classical function $f(x):\{0,1\}^n \rightarrow\{0,1\}$, where $n$ is the bit-size of the search space, find an input $x_0$ for which $f(x_0)=1$. The complexity of the algorithm is measured by the number of uses of the function $f(x)$. Classically, in the worst-case scenario, $f(x)$ has to be evaluated a total of $N-1$ times, where $N=2^n$, trying out all the possibilities. After $N-1$ elements, it must be the last element. Grover's quantum algorithm can solve this problem much faster, providing a quadratic speed up. Quadratic here implies that only about $\sqrt{N}$ evaluations would be required, compared to $N$.
Outline of the algorithm
Suppose there are $N=2^n$ eligible items for the search task and they are index by assigning each item an integer from $0$ to $N-1$. Further, suppose that there are $M$ different valid inputs, meaning that there are $M$ inputs for which $f(x)=1$. The steps of the algorithm are then as follows:
- Start with a register of $n$ qubits initialized in the state $\ket{0}$.
- Prepare the register into a uniform superposition by applying $H$ to each qubit of the register: $$|\text{register}\rangle=\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1}|x\rangle$$
- Apply the following operations to the register $N_{\text{optimal}}$ number of times:
- The phase oracle $O_f$ that applies a conditional phase shift of $-1$ for the solution items.
- Apply $H$ to each qubit in the register.
- A conditional phase shift of $-1$ to every computational basis state except $\ket{0}$. This can be represented by the unitary operation $-O_0$, as $O_0$ represents the conditional phase shift to $\ket{0}$ only.
- Apply $H$ to each qubit in the register.
- Measure the register to obtain the index of a item that's a solution with very high probability.
- Check if it's a valid solution. If not, start again.
$N_{\text{optimal}} = \left\lfloor \frac{\pi}{4}\sqrt{\frac{N}{M}}-\frac{1}{2} \right\rfloor$ is the optimal number of iterations that maximizes the likelihood of obtaining the correct item by measuring the register.
Note
The joint application of the steps 3.b, 3.c, and 3.d is usually known as Grover's diffusion operator.
The overall unitary operation applied to the register is:
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$
Following the register's state step by step
To illustrate the process, let's follow the mathematical transformations of the state of the register for a simple case in which there are only two qubits and the valid element is $\ket{01}.$
The register starts in the state:
$$\ket{\text{register}}=\ket{00}$$
After applying $H$ to each qubit the register's state transforms to:
$$\ket{\text{register}}= \frac{1}{\sqrt{4}} \sum_{i \in \lbrace 0,1 \rbrace}^2\ket{i}=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$
Then, the phase oracle is applied to get:
$$\ket{\text{register}} = \frac12(\ket{00}-\ket{01}+\ket{10}+\ket{11})$$
Then $H$ acts on each qubit again to give:
$$\ket{\text{register}} = \frac12(\ket{00}+\ket{01}-\ket{10}+\ket{11})$$
Now the conditional phase shift is applied on every state except $\ket{00}$:
$$\ket{\text{register}} = \frac12(\ket{00}-\ket{01}+\ket{10}-\ket{11})$$
Finally, the first Grover iteration ends by applying $H$ again to get:
$$\ket{\text{register}} = \ket{01}$$
By following the above steps, the valid item is found in a single iteration. As you will see later, this is because for N=4 and a single valid item, the optimal number of times is $N_{\text{optimal}} =1$.
Geometrical explanation
To see why Grover's algorithm works, let's study the algorithm from a geometrical perspective. Supposing there are $M$ valid solutions, the superposition of all quantum states that aren't a solution to the search problem:
$$\ket{\text{bad}}=\frac{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
The superposition of all states that are a solution to the search problem:
$$\ket{\text{good}}=\frac{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
Since good and bad are mutually exclusive sets because an item can't be valid and not valid, the states are orthogonal. Both states form the orthogonal basis of a plane in the vector space. One can use this plane to visualize the algorithm.
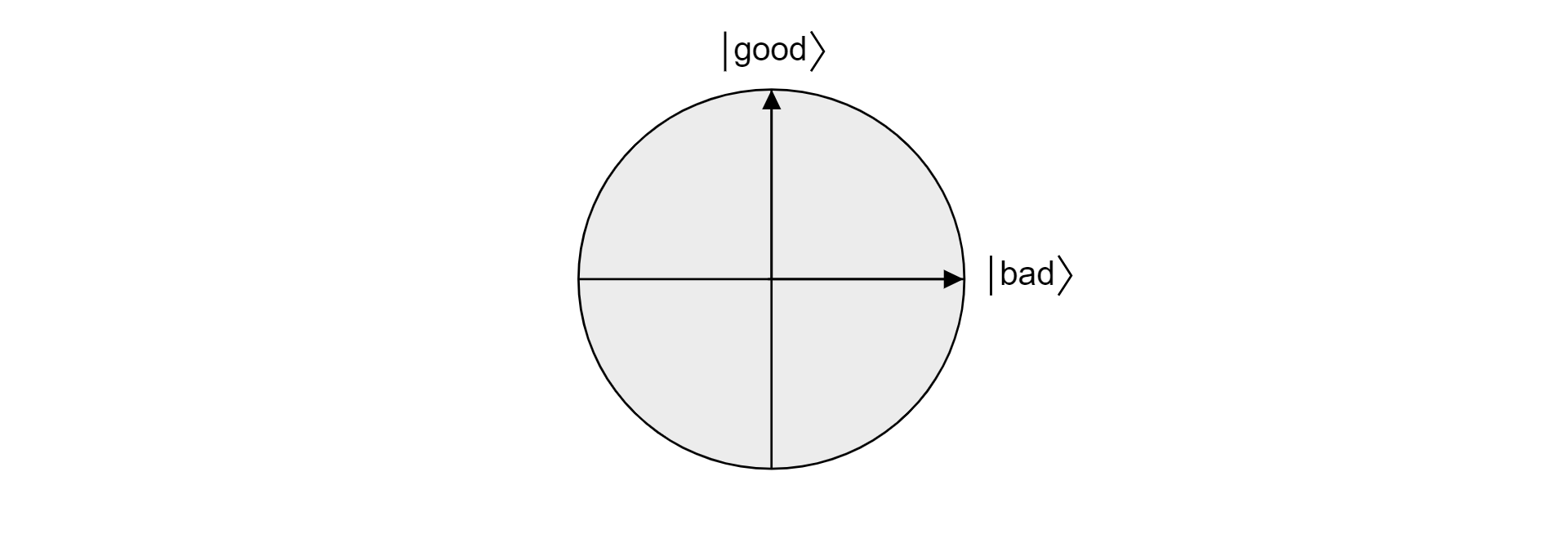
Now, suppose $\ket{\psi}$ is an arbitrary state that lives in the plane spanned by $\ket{\text{good}}$ and $\ket{\text{bad}}$. Any state living in that plane can be expressed as:
$$\ket{\psi} = \alpha \ket{\text{good}} + \beta \ket{\text{bad}}$$
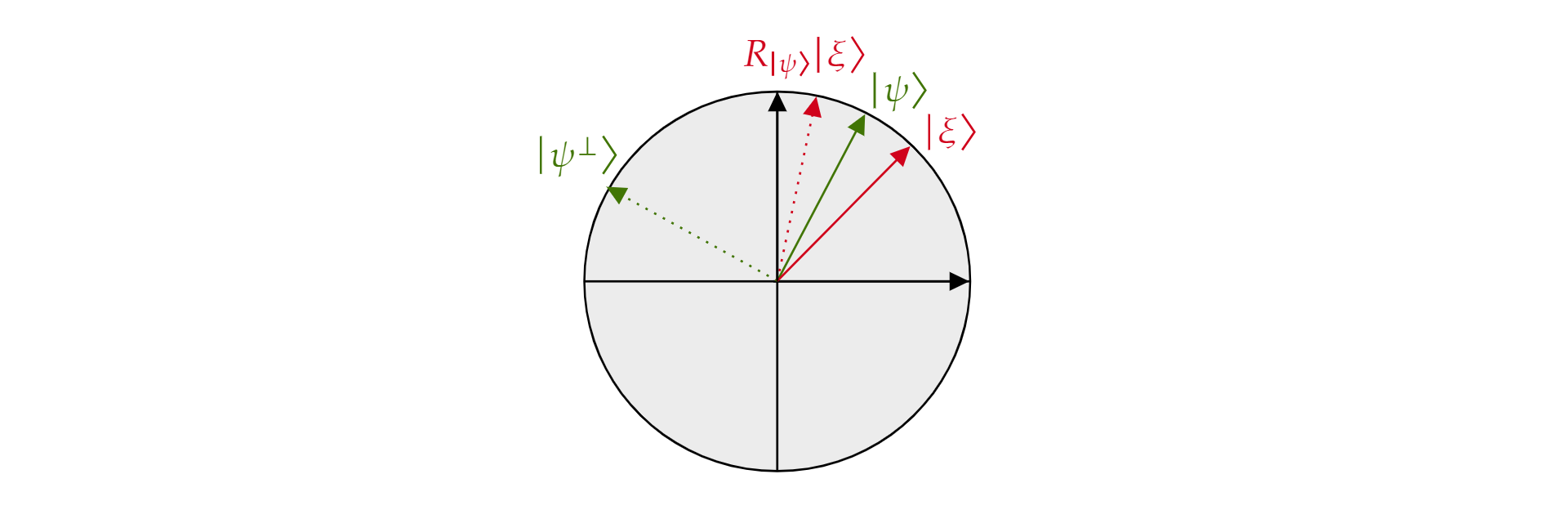
where $\alpha$ and $\beta$ are real numbers. Now, let's introduce the reflection operator $R_{\ket{\psi}}$, where $\ket{\psi}$ is any qubit state living in the plane. The operator is defined as:
$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$
It is called the reflection operator about $\ket{\psi}$ because it can be geometrically interpreted as reflection about the direction of $\ket{\psi}$. To see it, take the orthogonal basis of the plane formed by $\ket{\psi}$ and its orthogonal complement $\ket{\psi^{\perp}}$. Any state $\ket{\xi}$ of the plane can be decomposed in such basis:
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
If one applies the operator $R_{\ket{\psi}}$ to $\ket{\xi}$:
$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
The operator $R_{\ket{\psi}}$ inverts the component orthogonal to $\ket{\psi}$ but leaves the $\ket{\psi}$ component unchanged. Therefore, $R_{\ket{\psi}}$ is a reflection about $\ket{\psi}$.
Grover's algorithm, after the first application of $H$ to every qubit, starts with an uniform superposition of all states. This can be written as:
$$\ket{\text{all}} = \sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$
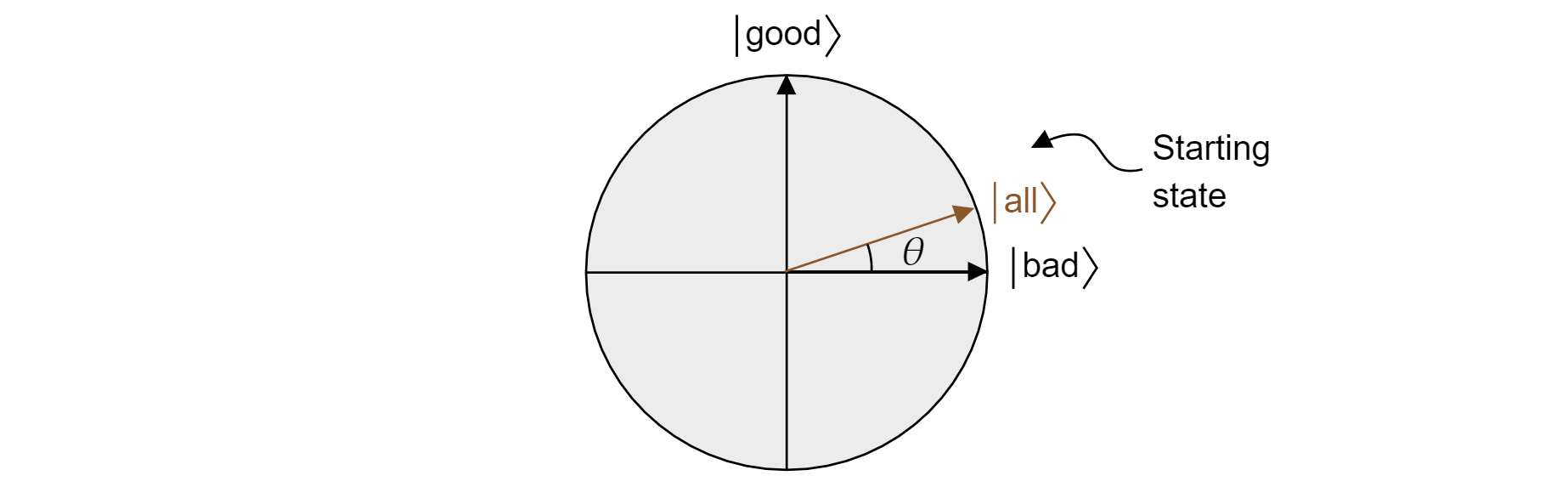
And thus the state lives in the plane. Note that the probability of obtaining a correct result when measuring from the equal superposition is just $|\bra{\text{good}}\ket{\text{all}}|^2=M/N$, which is what you would expect from a random guess.
The oracle $O_f$ adds a negative phase to any solution to the search problem. Therefore, it can be written as a reflection about the $\ket{\text{bad}}$ axis:
$$O_f = R_{\ket{\text{bad}}} = 2\ket{\text{bad}}\bra{\text{bad}} - \mathbb{I}$$
Analogously, the conditional phase shift $O_0$ is just an inverted reflection about the state $\ket{0}$:
$$O_{0} = R_{\ket{0}}= -2\ket{0}\bra{0} + \mathbb{I}$$
Knowing this fact, it's easy to check that the Grover diffusion operation $-H^{\otimes n} O_{0} H^{\otimes n}$ is also a reflection about the state $\ket{all}$. Just do:
$$-H^{\otimes n} O_{0} H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{0}H^{\otimes n} -H^{\otimes n}\mathbb{I}H^{\otimes n} = 2\ket{\text{all}}\bra{\text{all}} - \mathbb{I} = R_{\ket{\text{all}}}$$
It has been demonstrated that each iteration of Grover's algorithm is a composition of two reflections $R_{\ket{\text{bad}}}$ and $R_{\ket{\text{all}}}$.
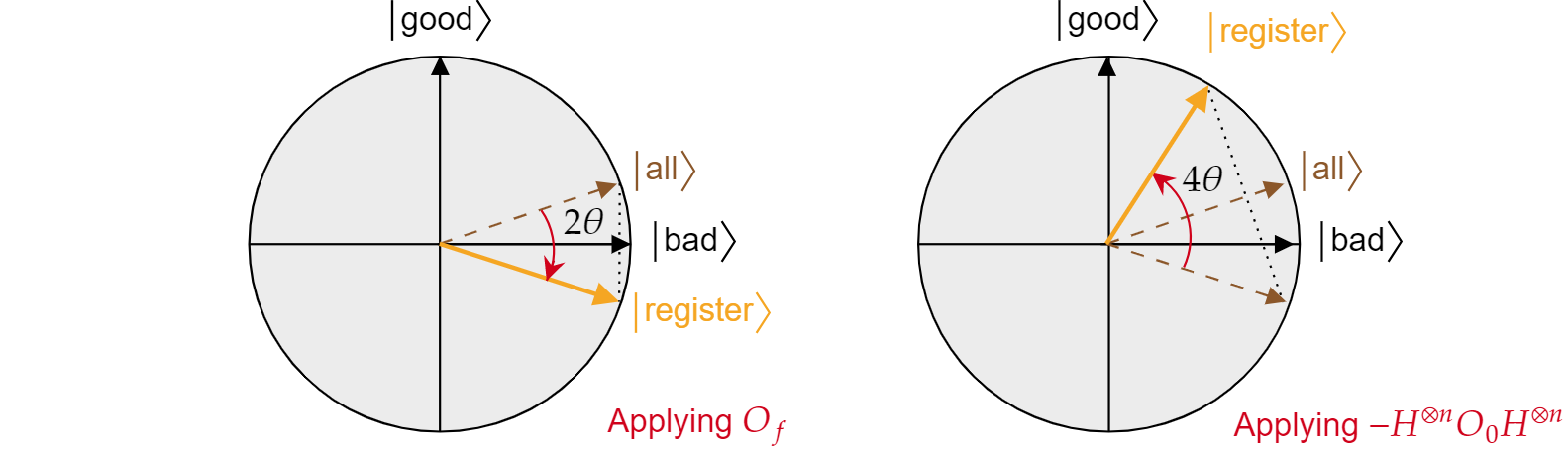
The combined effect of each Grover iteration is a counterclockwise rotation of an angle $2\theta$. Fortunately, the angle $\theta$ is easy to find. Since $\theta$ is just the angle between $\ket{\text{all}}$ and $\ket{\text{bad}}$, one can use the scalar product to find the angle. It is known that $\cos{\theta}=\braket{\text{all}|\text{bad}}$, so one needs to calculate $\braket{\text{all}|\text{bad}}$. From the decomposition of $\ket{\text{all}}$ in terms of $\ket{\text{bad}}$ and $\ket{\text{good}}$, it follows:
$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)} $$
The angle between the state of the register and the $\ket{\text{good}}$ state decreases with each iteration, resulting in a higher probability of measuring a valid result. To calculate this probability, you just need to calculate $|\braket{\text{good}|\text{register}}|^2$. The angle between $\ket{\text{good}}$ and $\ket{\text{register}}$ is denoted as $\gamma (k)$, where $k$ is the iteration count:
$$\gamma = \frac{\pi}{2}-\theta -2k\theta = \frac{\pi}{2} -(2k + 1) \theta $$
Therefore, the probability of success is:
$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
Optimal number of iterations
As the probability of success can be written as a function of the number of iterations, the optimal number of iterations $N_{\text{optimal}}$ can be found by computing the smallest positive integer that (approximately) maximizes the success probability function.
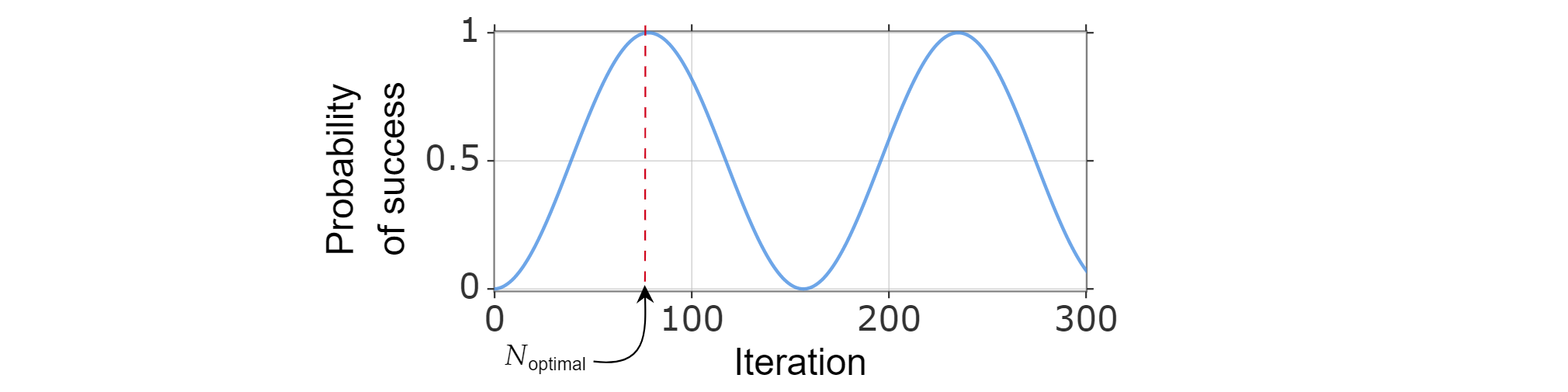
It is known that $\sin^2{x}$ reaches its first maximum for $x=\frac{\pi}{2}$, so:
$$\frac{\pi}{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}} \right)$$
This gives:
$$k_{\text{optimal}} = \frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 = \frac{\pi}{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$
Where in the last step, $\arccos \sqrt{1-x} = \sqrt{x} + O(x^{3/2})$.
Therefore, you can pick $N_{\text{optimal}} = \left\lfloor \frac{\pi}{4}\sqrt{\frac{N}{M}}-\frac{1}{2} \right\rfloor$.
Complexity analysis
From the previous analysis, $O\left(\sqrt{\frac{N}{M}}\right)$ queries of the oracle $O_f$ are needed to find a valid item. However, can the algorithm be implemented efficiently in terms of time complexity? $O_0$ is based on computing Boolean operations on $n$ bits and is known to be implementable using $O(n)$ gates. There are also two layers of $n$ Hadamard gates. Both of these components thus require only $O(n)$ gates per iteration. Because $N=2^n$, it follows that $O(n)=O(log(N))$. Therefore, if $O\left(\sqrt{\frac{N}{M}}\right)$ iterations and $O(log(N))$ gates per iteration are needed, the total time complexity (without taking into account the oracle implementation) is $O\left(\sqrt{\frac{N}{M}}log(N)\right)$.
The overall complexity of the algorithm ultimately depends on the complexity of the implementation of the oracle $O_f$. If a function evaluation is much more complicated on a quantum computer than on a classical one, the overall algorithm runtime will be longer in the quantum case, even though technically, it uses fewer queries.
References
If you want to continue learning about Grover's algorithm, you can check any of the following sources:
- Original paper by Lov K. Grover
- Quantum search algorithms section of Nielsen, M. A. & Chuang, I. L. (2010). Quantum Computation and Quantum Information.
- Grover's algorithm on Arxiv.org