Note
Access to this page requires authorization. You can try signing in or changing directories.
Access to this page requires authorization. You can try changing directories.
This article describes the role of T gates and T factories in fault tolerant quantum computing. Giving a quantum algorithm, the estimation of required resources for running the T gates and T factories becomes crucial to determine the feasibility of the algorithm. The Azure Quantum Resource Estimator calculates the number of T states needed to run the algorithm, the number of physical qubits for a single T factory, and the runtime of the T factory.
Universal set of quantum gates
According to DiVincenzo's criteria a scalable quantum computer must be able to implement a universal set of quantum gates. A universal set contains all the gates needed to perform any quantum computation, that is, any computation must decompose back into a finite sequence of universal gates. At a minimum, a quantum computer must be able to move single qubits to any position on the Bloch Sphere (using single-qubit gates), as well as introduce entanglement in the system, which requires a multi-qubit gate.
There are only four functions that map one bit to one bit on a classical computer. In contrast, there are an infinite number of unitary transformations on a single qubit on a quantum computer. Therefore, no finite set of primitive quantum operations or gates, can exactly replicate the infinite set of unitary transformations allowed in quantum computing. This means, unlike classical computing, it is impossible for a quantum computer to implement every possible quantum program exactly using a finite number of gates. Thus quantum computers cannot be universal in the same sense of classical computers. As a result, when we say that a set of gates is universal for quantum computing we actually mean something slightly weaker than we mean with classical computing.
For universality, it's required that a quantum computer only approximates every unitary matrix within a finite error using a finite length gate sequence.
In other words, a set of gates is a universal gate set if any unitary transformation can be approximately written as a product of gates from this set. It's required that for any prescribed error bound, there exist gates $G_{1}, G_{2}, \ldots, G_N$ from the gate set such that
$$ G_N G_{N-1} \cdots G_2 G_1 \approx U. $$
Because the convention for matrix multiplication is to multiply from right to left the first gate operation in this sequence, $G_N$, is actually the last one applied to the quantum state vector. More formally, such a gate set is said to be universal if for every error tolerance $\epsilon>0$ there exists $G_1, \ldots, G_N$ such that the distance between $G_N\ldots G_1$ and $U$ is at most $\epsilon$. Ideally the value of $N$ needed to reach this distance of $\epsilon$ should scale poly-logarithmically with $1/\epsilon$.
For example, the set formed by Hadamard, CNOT and T gates is a universal set, from which any quantum computation (on any number of qubits) can be generated. The Hadamard and the T gate set generates any single-qubit gate:
$$ H=\frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix}, \qquad T=\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4} \end{bmatrix}. $$
In a quantum computer, quantum gates can be classified into two categories: Clifford gates and non-Clifford gates, in this case, the T gate. Quantum programs made from only Clifford gates can be simulated efficiently using a classical computer, and therefore, non-Clifford gates are required to obtain quantum advantage. In many quantum error correction (QEC) schemes the so-called Clifford gates are easy to implement, that is they require very few resources in terms of operations and qubits to implement fault tolerantly, whereas non-Clifford gates are quite costly when requiring fault tolerance. In a universal quantum gate set, the T gate is commonly used as the non-Clifford gate.
The standard set of single-qubit Clifford gates, included by default in Q#, include
$$ H=\frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 &1 \\ 1& 0 \end{bmatrix}= HT^4H, $$
$$ Y = \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&0\\ 0&-1 \end{bmatrix}=T^4. $$
Together with the non-Clifford gate (the T gate), these operations can be composed to approximate any unitary transformation on a single qubit.
T factories in the Azure Quantum Resource Estimator
The non-Clifford T gate preparation is crucial because the other quantum gates are not sufficient for universal quantum computation. To implement non-Clifford operations for practical-scale algorithms, low error rate T gates (or T states) is required. However, they can be difficult to directly implement on logical qubits, and can also be difficult for some physical qubits.
In a fault tolerant quantum computer, the required low error rate T states are produced using a T state distillation factory, or T factory for short. These T factories typically involve a sequence of rounds of distillation, where each round takes in many noisy T states encoded in a smaller distance code, processes them using a distillation unit, and outputs fewer less noisy T states encoded in a larger distance code, with the number of rounds, distillation units, and distances all being parameters which can be varied. This procedure is iterated, where the output T states of one round are fed into the next round as inputs.
Based on the duration of the T factory, the Azure Quantum Resource Estimator determines how often a T factory can be invoked before it exceeds the total runtime of the algorithm, and thus how many T states can be produced during the algorithm runtime. Usually, more T states are required than what can be produced within the invocations of a single T factory during the algorithm runtime. In order to produce more T states, the Resource Estimator uses copies of the T factories.
T factory physical estimation
The Resource Estimator calculates the total number of T states needed to run the algorithm, and the number of physical qubits for a single T factory and its runtime.
The goal is to produce all T states within the algorithm runtime with as few T factory copies as possible. The following diagram shows an example of the runtime of the algorithm and the runtime of one T factory. You can see that the runtime of the T factory is shorter than the runtime of the algorithm. In this example, one T factory can distill one T state. Two questions arise:
- How often can the T factory be invoked before the end of the algorithm?
- How many copies of the T factory distillation round are necessary to create the number of T states required during the algorithm's runtime?
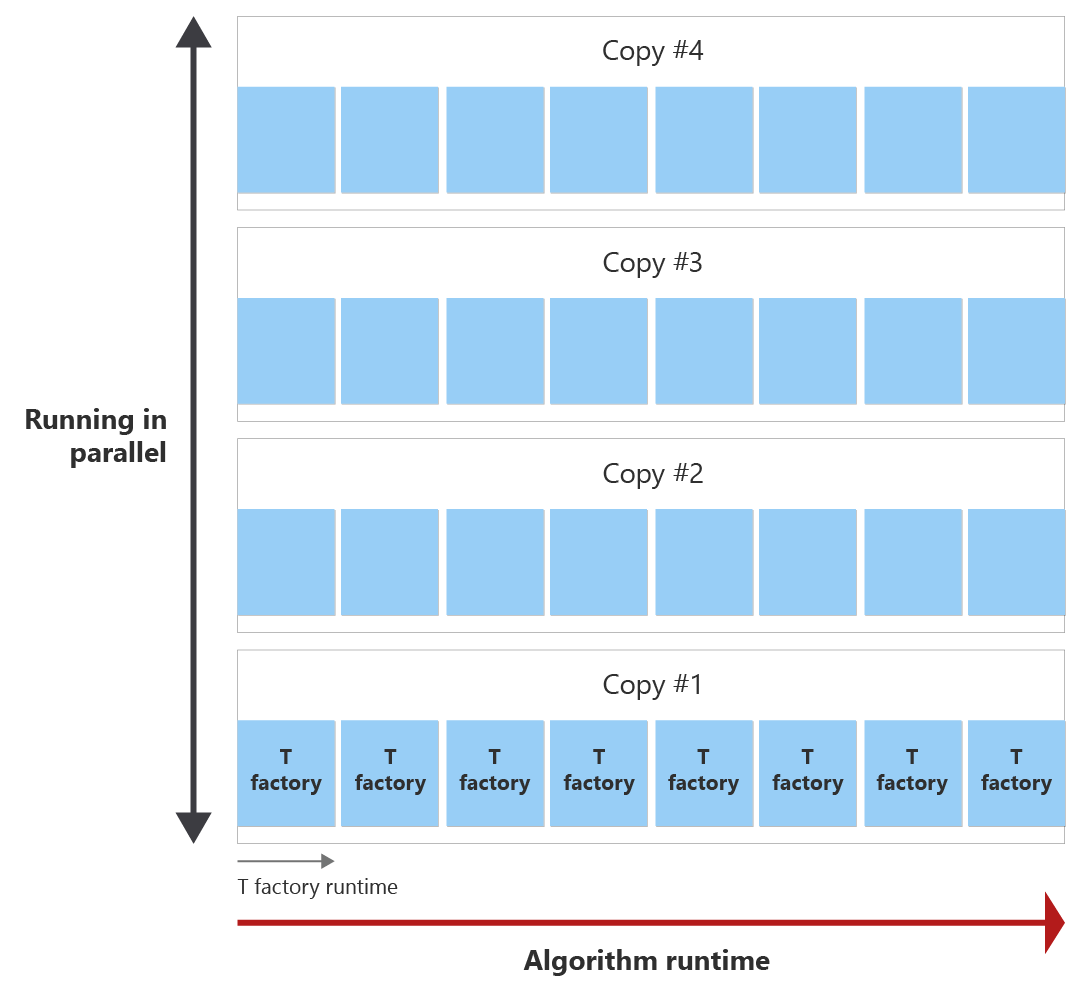
Before the end of the algorithm, the T factory can be invoked eight times, which is called a distillation round. For example, if you need 30 T states, a single T factory is invoked eight times during runtime of the algorithm and thus, it creates eight T states. Then you need four copies of the T factory distillation round running in parallel to distill the 30 T states needed.
Note
Note that T factory copies and T factory invocations aren't the same.
The T state distillation factories are implemented in a sequence of rounds, where each round consists of a set of copies of distillation units running in parallel. The Resource Estimator calculates how many physical qubits are needed to run one T factory and for how long the T factory runs, among other required parameters.
You can only do full invocations of a T factory. Therefore, there may be situations in which the accumulated runtime of all T factory invocations is less than the algorithm runtime. Since qubits are reused by different rounds, the number of physical qubits for one T factory is the maximum number of physical qubits used for one round. The runtime of the T factory is the sum of the runtime in all rounds.
Note
If the physical T gate error rate is lower than the required logical T state error rate, the Resource Estimator cannot perform a good resource estimation. When you submit a resource estimation job, you may encounter that the T factory cannot be found because the required logical T state error rate is either too low or too high.
For more information, see Appendix C of Assessing requirements to scale to practical quantum advantage.