Note
Access to this page requires authorization. You can try signing in or changing directories.
Access to this page requires authorization. You can try changing directories.
In this tutorial, you write a Q# program that prepares two qubits in a specific quantum state, operates on the qubits to entangle them with each other, and performs measurements to demonstrate the effects of superposition and entanglement. You build your Q# program piece-by-piece to introduce qubit states, quantum operations, and measurements.
Before you begin, review the following quantum computing concepts:
- Classical bits hold a single binary value such as a 0 or 1, but qubits can be in a superposition of the two states, 0 and 1. Each possible qubit state is described by a set of probability amplitudes.
- When you measure a qubit's state, you always get either 0 or 1. The probability of each result is determined by the probability amplitudes that define the superposition state when you make a measurement.
- Multiple qubits can be entangled such that you can't describe them independently from each other. When you measure one qubit in an entangled pair, you also get information about the other qubit without measuring it.
In this tutorial, you learn how to:
- Create Q# operations to initialize a qubit to a desired state.
- Put a qubit into a superposition state.
- Entangle a pair of qubits.
- Measure a qubit and observe the results.
Tip
If you want to accelerate your quantum computing journey, check out Code with Azure Quantum, a unique feature of the Microsoft Quantum website. Here, you can run built-in Q# samples or your own Q# programs, generate new Q# code from your prompts, open and run your code in VS Code for the Web with one click, and ask Copilot questions about quantum computing.
Prerequisites
To run the code sample with Copilot for Azure Quantum, you must have a Microsoft (MSA) email account.
For more information about Copilot for Azure Quantum, see Explore Azure Quantum.
Initialize a qubit to a known state
The first step is to define a Q# operation that initializes a qubit to a desired classical state, either 0 or 1. This operation measures a qubit in a general quantum state, which returns a Q# Result type value of either Zero or One. If the measurement result is different from the desired state, then the operation flips the state so that the operation returns the desired state 100% of the time.
Open Copilot for Azure Quantum, clear the default code, and then copy the following code into the code editor window. You can't run this code by itself because it isn't a complete Q# program yet.
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
The code example introduces two standard Q# operations, M and X, that transform the state of a qubit.
Here's a detailed description of how the SetQubitState operation works:
- Takes two parameters: a
Resulttype parameter nameddesiredthat represents the desired state for the qubit to be in (ZeroorOne), and aQubittype parameter. - Performs a measurement operation,
M, which measures the state of the qubit (ZeroorOne) and compares the result to the value that you pass fordesired. - If the measurement result doesn't match the value for
desired, then anXoperation is applied to the qubit. This operation flips the state of the qubit so that the measurement probabilities forZeroandOneare reversed.
Write a test operation to test the Bell state
To call the SetQubitState operation in your Q# program, create another operation named Main. This operation allocates two qubits, calls SetQubitState to set the first qubit to a known state, and then measures the qubits to see the results.
Copy the following code into the code editor window, after the SetQubitState operation.
operation Main() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = One;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
numOnesQ1 += 1;
}
if resultQ2 == One {
numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
In the code, the count and initial variables are set to 1000 and One respectively. This initializes the first qubit to One and measures each qubit 1000 times.
The Main operation does the following:
- Sets variables for the number of shots (
count) and the initial qubit state (One). - Calls the
usestatement to initialize two qubits. - Loops over the experiment
counttimes. - In the loop, calls
SetQubitStateto set the specifiedinitialvalue on the first qubit, and then callsSetQubitStateagain to set the second qubit to theZerostate. - In the loop, applies the
Moperation to measure each qubit, and then stores the number of measurements for each qubit that returnOne. - After the loop completes, calls
SetQubitStateagain to reset the qubits to a known state (Zero). You must reset qubits that you allocate with theusestatement. - Calls the
Messagefunction to print your results in the output window.
Run the code in Copilot for Azure Quantum
Before you write code for superposition and entanglement, test your current program to see the initialization and measurement of the qubits.
To run your code as a standalone program, the Q# compiler in Copilot needs to know where to start the program. Because you didn't specify a namespace, the compiler recognizes the default entry point as the Main operation. For more information, see Projects and implicit namespaces.
Your Q# program now looks like this:
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
operation Main() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = One;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
numOnesQ1 += 1;
}
if resultQ2 == One {
numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
Copy and paste the complete code sample into the Copilot for Azure Quantum code window, set the slider for the number of shots to "1", and then choose Run. The results display in the histogram and in the Results fields.
Q1 - Zeros: 0
Q1 - Ones: 1000
Q2 - Zeros: 1000
Q2 - Ones: 0
Your program doesn't modify the qubit states yet, so measurement of the first qubit always returns One, and the second qubit always returns Zero.
If you change the value of initial to Zero and run the program again, then the first qubit also always returns Zero.
Q1 - Zeros: 1000
Q1 - Ones: 0
Q2 - Zeros: 1000
Q2 - Ones: 0
Put a qubit into a superposition state
Currently, the qubits in your program are in a classical state, either 1 or 0, just like bits on a regular computer. To entangle the qubits, you must first put one of the qubits into an equal superposition state. Measurement of a qubit in an equal superposition state has a 50% to return Zero and a 50% chance to return One.
To put a qubit into a superposition state, use the Q# H, or Hadamard, operation. The H operation converts a qubit that's in a pure Zero or One state into a sort of halfway state between Zero and One.
Modify your code in the Main operation. Reset the initial value to One and insert a line for the H operation:
for test in 1..count {
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
H(q1); // Add the H operation after initialization and before measurement
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
...
Run your program again. Because the first qubit is in an equal superposition when you measure it, you get close to a 50/50 result for Zero and One. For example, your output looks similar to this:
Q1 - Zeros: 523
Q1 - Ones: 477
Q2 - Zeros: 1000
Q2 - Ones: 0
Every time you run the program, the results for the first qubit vary slightly, but are close to 50% One and 50% Zero, while the results for the second qubit are still always Zero.
Initialize the first qubit to Zero instead of One and run the program again. You get similar results because the H operation turns both a pure Zero state and a pure One state into an equal superposition state.
Note
To see how the superposition results vary over the distribution of the shots, move the slider in Copilot for Azure Quantum and increase the number of shots.
Entangle two qubits
Entangled qubits are correlated such that they can't be described independently from each other. When you measure the state of one entangled qubit, you also know the state of the other qubit without measuring it. This tutorial uses an example with two entangled qubits, but you can entangle three or more qubits too.
To create an entangled state, use the Q# CNOT, or Controlled-NOT, operation. When you apply CNOT to two qubits, one qubit is the control qubit and the other is the target qubit. If the state of the control qubit is One, then the CNOT operation flips the state of the target qubit. Otherwise, CNOT does nothing to the qubits.
Add the CNOT operation to your program immediately after the H operation. Your full program looks like this:
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
operation Main() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = Zero;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
H(q1);
CNOT(q1, q2); // Add the CNOT operation after the H operation
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
numOnesQ1 += 1;
}
if resultQ2 == One {
numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
Run the program and view the output. Your results very slightly each time you run the program.
Q1 - Zeros: 502
Q1 - Ones: 498
Q2 - Zeros: 502
Q2 - Ones: 498
The statistics for the first qubit still show about a 50% chance to measure both One and Zero, but the measurement results for the second qubit aren't always Zero now. Each qubit has the same number of Zero results and One results. The measurement result for the second qubit is always the same as the result for the first qubit because the two qubits are entangled. If the first qubit is measured to be Zero, then the entangled qubit must also be Zero. If the first qubit is measured to be One, then the entangled qubit must also be One.
Prerequisites
To develop and run the code sample in your local development environment, install the following tools:
- The latest version of Visual Studio Code (VS Code) or open VS Code for the Web.
- The latest version of the Azure Quantum Development Kit (QDK) extension. For installation details, see Set up the QDK extension.
Create a new Q# file
- In VS Code, open the File menu and choose New Text File to create a new file.
- Save the file as
CreateBellStates.qs. This file is where you write the Q# code for your program.
Initialize a qubit to a known state
The first step is to define a Q# operation that initializes a qubit to a desired classical state, either 0 or 1. This operation measures a qubit in a general quantum state, which returns a Q# Result type value of either Zero or One. If the measurement result is different from the desired state, then the operation flips the state so that the operation returns the desired state 100% of the time.
Open CreateBellStates.qs and copy the following code:
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
The code example introduces two standard Q# operations, M and X, that transform the state of a qubit.
Here's a detailed description of how the SetQubitState operation works:
- Takes two parameters: a
Resulttype parameter nameddesiredthat represents the desired state for the qubit to be in (ZeroorOne), and aQubittype parameter. - Performs a measurement operation,
M, which measures the state of the qubit (ZeroorOne) and compares the result to the value that you pass fordesired. - If the measurement result doesn't match the value for
desired, then anXoperation is applied to the qubit. This operation flips the state of the qubit so that the measurement probabilities forZeroandOneare reversed.
Write a test operation to test the Bell state
To call the SetQubitState operation in your Q# program, create another operation named Main. This operation allocates two qubits, calls SetQubitState to set the first qubit to a known state, and then measures the qubits to see the results.
Add the following operation to your CreateBellStates.qs file after the SetQubitState operation:
operation Main() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = One;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
numOnesQ1 += 1;
}
if resultQ2 == One {
numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
In the code, the count and initial variables are set to 1000 and One respectively. This initializes the first qubit to One and measures each qubit 1000 times.
The Main operation does the following:
- Sets variables for the number of shots (
count) and the initial qubit state (One). - Calls the
usestatement to initialize two qubits. - Loops over the experiment
counttimes. - In the loop, calls
SetQubitStateto set the specifiedinitialvalue on the first qubit, and then callsSetQubitStateagain to set the second qubit to theZerostate. - In the loop, applies the
Moperation to measure each qubit, and then stores the number of measurements for each qubit that returnOne. - After the loop completes, calls
SetQubitStateagain to reset the qubits to a known state (Zero). You must reset qubits that you allocate with theusestatement. - Calls the
Messagefunction to print your results in the console.
Run the code
Before you write code for superposition and entanglement, test your current program to see the initialization and measurement of the qubits.
To run the code as a standalone program, the Q# compiler needs to know where to start the program. Because you didn't specify a namespace, the compiler recognizes the default entry point as the Main operation. For more information, see Projects and implicit namespaces.
Your CreateBellStates.qs file now looks like this:
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
operation Main() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = One;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
numOnesQ1 += 1;
}
if resultQ2 == One {
numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
To run the program, choose the Run command from the code lens that precedes the Main operation, or enter Ctrl + F5. The program runs the Main operation on the default simulator.
Your output appears in the debug console.
Q1 - Zeros: 0
Q1 - Ones: 1000
Q2 - Zeros: 1000
Q2 - Ones: 0
Your program doesn't modify the qubit states yet, so measurement of the first qubit always returns One, and the second qubit always returns Zero.
If you change the value of initial to Zero and run the program again, then the first qubit also always returns Zero.
Q1 - Zeros: 1000
Q1 - Ones: 0
Q2 - Zeros: 1000
Q2 - Ones: 0
Put a qubit into a superposition state
Currently, the qubits in your program are in a classical state, either 1 or 0, just like bits on a regular computer. To entangle the qubits, you must first put one of the qubits into an equal superposition state. Measurement of a qubit in an equal superposition state has a 50% to return Zero and a 50% chance to return One.
To put a qubit into a superposition state, use the Q# H, or Hadamard, operation. The H operation converts a qubit that's in a pure Zero or One state into a sort of halfway state between Zero and One.
Modify your code in the Main operation. Reset the initial value to One and insert a line for the H operation:
for test in 1..count {
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
H(q1); // Add the H operation after initialization and before measurement
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
...
Run your program again. Because the first qubit is in an equal superposition when you measure it, you get close to a 50/50 result for Zero and One. For example, your output looks similar to this:
Q1 - Zeros: 523
Q1 - Ones: 477
Q2 - Zeros: 1000
Q2 - Ones: 0
Every time you run the program, the results for the first qubit vary slightly, but are close to 50% One and 50% Zero, while the results for the second qubit are still always Zero.
Initialize the first qubit to Zero instead of One and run the program again. You get similar results because the H operation turns both a pure Zero state and a pure One state into an equal superposition state.
Entangle two qubits
Entangled qubits are correlated such that they can't be described independently from each other. When you measure the state of one entangled qubit, you also know the state of the other qubit without measuring it. This tutorial uses an example with two entangled qubits, but you can entangle three or more qubits too.
To create an entangled state, use the Q# CNOT, or Controlled-NOT, operation. When you apply CNOT to two qubits, one qubit is the control qubit and the other is the target qubit. If the state of the control qubit is One, then the CNOT operation flips the state of the target qubit. Otherwise, CNOT does nothing to the qubits.
Add the CNOT operation to your program immediately after the H operation. Your full program looks like this:
operation SetQubitState(desired : Result, target : Qubit) : Unit {
if desired != M(target) {
X(target);
}
}
operation Main() : (Int, Int, Int, Int) {
mutable numOnesQ1 = 0;
mutable numOnesQ2 = 0;
let count = 1000;
let initial = Zero;
// allocate the qubits
use (q1, q2) = (Qubit(), Qubit());
for test in 1..count {
SetQubitState(initial, q1);
SetQubitState(Zero, q2);
H(q1);
CNOT(q1, q2); // Add the CNOT operation after the H operation
// measure each qubit
let resultQ1 = M(q1);
let resultQ2 = M(q2);
// Count the number of 'Ones' returned:
if resultQ1 == One {
numOnesQ1 += 1;
}
if resultQ2 == One {
numOnesQ2 += 1;
}
}
// reset the qubits
SetQubitState(Zero, q1);
SetQubitState(Zero, q2);
// Display the times that |0> is returned, and times that |1> is returned
Message($"Q1 - Zeros: {count - numOnesQ1}");
Message($"Q1 - Ones: {numOnesQ1}");
Message($"Q2 - Zeros: {count - numOnesQ2}");
Message($"Q2 - Ones: {numOnesQ2}");
return (count - numOnesQ1, numOnesQ1, count - numOnesQ2, numOnesQ2 );
}
Run the program and view the output. Your results very slightly each time you run the program.
Q1 - Zeros: 502
Q1 - Ones: 498
Q2 - Zeros: 502
Q2 - Ones: 498
The statistics for the first qubit still show about a 50% chance to measure both One and Zero, but the measurement results for the second qubit aren't always Zero now. Each qubit has the same number of Zero results and One results. The measurement result for the second qubit is always the same as the result for the first qubit because the two qubits are entangled. If the first qubit is measured to be Zero, then the entangled qubit must also be Zero. If the first qubit is measured to be One, then the entangled qubit must also be One.
Plot the frequency histogram
To plot a frequency histogram that shows the distribution of results when you run your program multiple times, complete the following steps:
Open your
CreateBellStates.qsfile in VS Code.Open the View menu and choose Command Palette.
Enter histogram to bring up the QDK: Run file and show histogram option. Or, choose the Histogram command from the code lens option that precedes the
Mainoperation. Then, enter a number of shots (for example, 100). The Q# histogram opens in a new tab.Each bar in the histogram corresponds to a possible outcome when the entanglement circuit runs 1000 times. The height of a bar represents the number of times that outcome occurs. For example, the following histogram shows a distribution with 50 unique results. Note that for each outcome, the measurement results for the first and the second qubit are always the same.
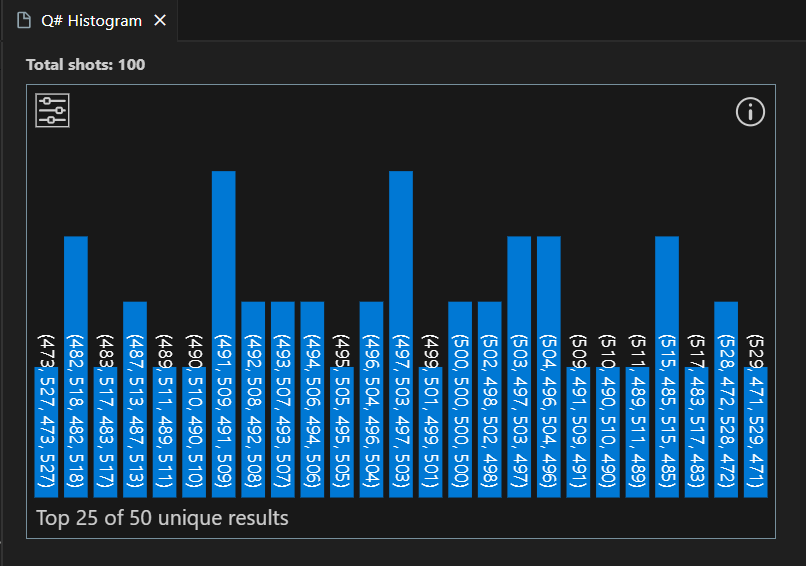
Tip
To zoom in on the histogram, use the mouse scroll wheel or a trackpad gesture. To pan the chart when you're zoomed in, hold Alt while you scroll.
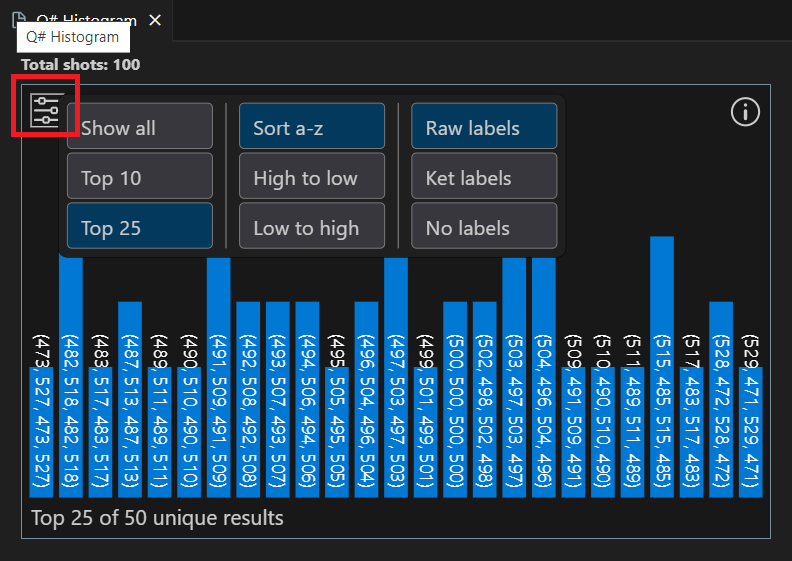
Choose a bar to display the percentage of total shots that produced that outcome.
Choose the settings icon in the top-left to display visualization options.
Run the code again, but this time with 1000 shots. As the number of shots increases, the distribution of results approaches a normal distribution.
Related content
Explore other Q# tutorials:
- Grover's search algorithm shows how to write a Q# program that uses Grover's search algorithm.
- Quantum Fourier Transform explores how to write a Q# program that directly addresses specific qubits.
- The Quantum Katas are self-paced tutorials and programming exercises that teach the elements of quantum computing and Q# programming at the same time.