What is superposition in quantum computing?
In the classical world, real objects like the cat and the box can only be in one state at a time. But in the quantum world, particles can exist in a superposition of all their possible states.
Unfortunately, there aren't any quantum computers that use cats to perform calculations. Instead, actual quantum computers use qubits, short for quantum bits. Just like how a bit is the basic unit of information in classical computing, a qubit is the basic unit of information in quantum computing. And just like how bits can take either one of two possible values, 0 and 1, a qubit also has a value of 0 or 1 when we measure it.
There are many physical representations of qubits. For example, the polarization of a photon or the spin of an electron can both be used as qubits because photons have two distinct polarization states and electrons have two distinct spin states when we measure them. We can represent one of those states as 0 and the other state as 1, and the qubit will always give 0 or 1 when we measure it.
But how do we represent superposition in a qubit? And what is the probability that we find a qubit to be in a particular state when we take a measurement?
Bloch sphere representation of superposition for single qubits
A qubit is a quantum particle that is in one of two possible states when we measure the qubit. Regardless of the physical nature of the qubit, we label the two states as 0 and 1. A qubit can be in the state 0, in the state 1, or in an infinite number of superpositions of both the 0 and 1 states. How do we represent these superpositions in quantum computing?
A helpful geometric representation of the superposition state of a single qubit is the Bloch sphere.
Imagine that you draw a circle with a unit radius (radius length equal to 1). Then, draw a vertical and horizontal axis such that the two axes intersect at the center of the circle. Now, let's define the 0 state to be where the vertical axis meets the top of the circle and the 1 state to be where the vertical axis meets the bottom of the circle. On this circle, the 0 and 1 states are $180^\circ$, or $\pi$ radians, from each other.
How does this representation relate to the state of a qubit? We can represent the qubit's state with an arrow (or vector) of unit length that's drawn from the center of the circle to the edge of the circle. When the vector points vertically up, the qubit is in the 0 state, and when the vector points vertically down, the qubit is in the 1 state. In this representation, a classical bit would be a vector that is always pointing straight up or straight down, but never in any other direction.
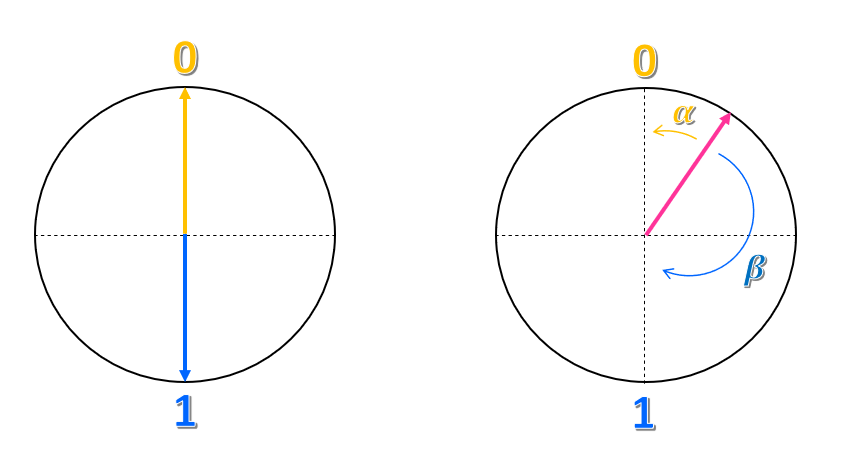
For a qubit, the vector can point anywhere on the circle. Each location on the circle, other than straight up or straight down, represents a superposition state. For example, we call the angle that the vector makes with the 0 state $\alpha$, and the angle that the vector makes with the 1 state $\beta$. Then, we represent the superposition state of the qubit as $\alpha 0 + \beta 1$.
Similar to the example of the cat and the box, the superposition state of a qubit is the sum of the individual states, 0 and 1, weighted by the numbers $\alpha$ and $\beta$. However, in the cat-and-box system the weights are real numbers, but in the qubit system the weights $\alpha$ and $\beta$ are complex numbers.
Because the amplitudes $\alpha$ and $\beta$ are complex numbers, we need another circle in our diagram that's in a plane perpendicular to the first circle to truly represent any superposition state of the qubit. These two circles exist in three dimensions to produce the Bloch sphere.
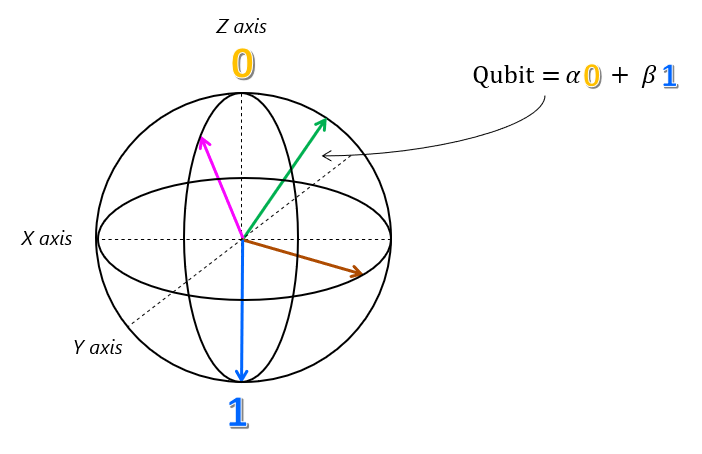
This Bloch sphere is an accurate geometrical representation of every possible superposition state for a single qubit. The qubit state is represented by the location on the sphere's surface that the vector points at. As useful as the Bloch sphere is, it unfortunately can't be extended to systems with multiple qubits.
Tip
The Bloch sphere is a powerful tool because the operations that we perform on a qubit during quantum computation are represented as rotations about one of the Bloch sphere's cardinal axes. This geometric representation helps to build intuition about how operations work in quantum computing, but it's challenging to use this intuition to design and describe algorithms. Q# helps by providing a language to describe such rotations.
What is the probability of finding a qubit in a particular state?
In the cat-and-box system from the previous unit, the weights for each state are real numbers that directly correspond to the probability that we find the system in each state. In the qubit system, the numbers $\alpha$ and $\beta$ are in general complex numbers that don't directly give the probabilities of finding the qubit in the 0 and 1 states. Instead, these numbers are called probability amplitudes (or just amplitudes).
The actual probabilities are calculated from the squares of the magnitudes of the probability amplitudes. The probability that a measurement finds the qubit in the 0 state is $|\alpha|^2$, and the probability that a measurement finds the qubit in the 1 state is $|\beta|^2$. In general, $\alpha + \beta$ doesn't sum to 100%, but $|\alpha|^2 + |\beta|^2$ always does. The constraint that $|\alpha|^2 + |\beta|^2 = 1$ is called the normalization condition, and every valid quantum state must meet this condition.