What is classification?
Binary classification is classification with two categories. For example, we could label patients as non-diabetic or diabetic.
The class prediction is made by determining the probability for each possible class as a value between 0 (impossible) and 1 (certain). The total probability for all classes is always 1, as the patient is definitely either diabetic or non-diabetic. So, if the predicted probability of a patient being diabetic is 0.3, then there's a corresponding probability of 0.7 that the patient is non-diabetic.
A threshold value, often 0.5, is used to determine the predicted class. If the positive class (in this case, diabetic) has a predicted probability greater than the threshold, then a classification of diabetic is predicted.
Training and evaluating a classification model
Classification is an example of a supervised machine learning technique, which means it relies on data that includes known feature values and known label values. In this example, the feature values are diagnostic measurements for patients, and the label values are a classification of non-diabetic or diabetic. A classification algorithm is used to fit a subset of the data into a function that can calculate the probability for each class label from the feature values. The remaining data is used to evaluate the model by comparing the predictions it generates from the features to the known class labels.
A simple example
Let's explore an example to help explain the key principles. Suppose we have the following patient data, which consists of a single feature (blood glucose level) and a class label 0 for non-diabetic, 1 for diabetic.
| Blood-Glucose | Diabetic |
|---|---|
| 82 | 0 |
| 92 | 0 |
| 112 | 1 |
| 102 | 0 |
| 115 | 1 |
| 107 | 1 |
| 87 | 0 |
| 120 | 1 |
| 83 | 0 |
| 119 | 1 |
| 104 | 1 |
| 105 | 0 |
| 86 | 0 |
| 109 | 1 |
We use the first eight observations to train a classification model, and we start by plotting the blood glucose feature (x) and the predicted diabetic label (y).
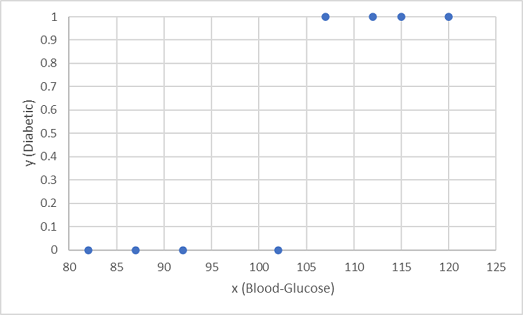
What we need is a function that calculates a probability value for y based on x (in other words, we need the function f(x) = y). You can see from the chart that patients with a low blood-glucose level are all non-diabetic, while patients with a higher blood-glucose level are diabetic. It seems like the higher the blood-glucose level, the more probable it is that a patient is diabetic, with the inflection point being somewhere between 100 and 110. We need to fit a function that calculates a value between 0 and 1 for y to these values.
One such function is a logistic function, which forms a sigmoidal (S-shaped) curve.
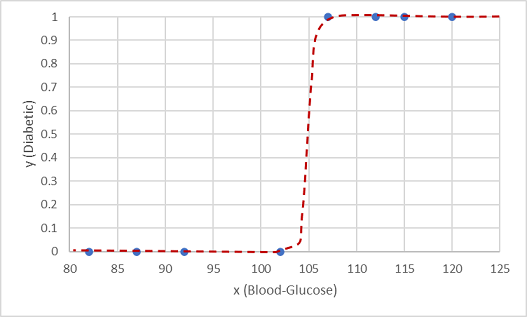
Now we can use the function to calculate a probability value that y is positive, meaning the patient is diabetic, from any value of x by finding the point on the function line for x. We can set a threshold value of 0.5 as the cut-off point for the class label prediction.
Let's test it with the two data values we held back.
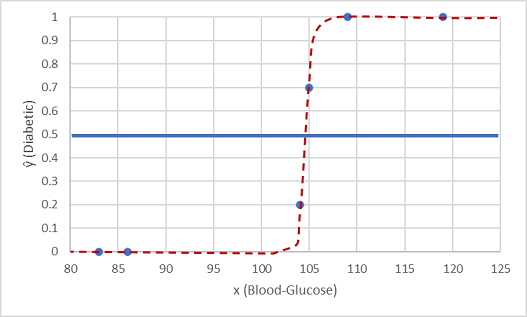
Points plotted below the threshold line yield a predicted class of 0 (non-diabetic) and points above the line are predicted as 1 (diabetic).
Now we can compare the label predictions (ŷ, or "y-hat"), based on the logistic function encapsulated in the model, to the actual class labels (y).
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |