Compartir a través de

Información general sobre transformaciones

  • Artículo

En este tema se describen los conceptos básicos de las transformaciones de Direct2D e incluye ejemplos de diversas transformaciones. Contiene las siguientes partes:

¿Qué es una transformación de Direct2D?

Una transformación especifica cómo asignar los puntos de un objeto de un espacio de coordenadas a otro o desde una posición a otra dentro del mismo espacio de coordenadas. Esta asignación se describe mediante una matriz de transformación, definida como una colección de tres filas con tres columnas de valores FLOAT, como se muestra en la tabla siguiente.

     
M11Default: 1.0 M12Default: 0.0 0,0
M21Default: 0.0 M22Default: 1.0 0,0
M31OffsetX: 0.0 M32OffsetY: 0.0 1.0

 

En esta matriz, los miembros M11, M12, M21 y M22 definen una transformación lineal que puede escalar, girar o sesgar un objeto; Los miembros OffsetX y OffsetY definen la traducción que se aplicará después de que se haya realizado la transformación lineal. Para las transformaciones affine, los valores de la tercera columna siempre son 0,0, 0,0 y 1,0.

Dado que Direct2D solo admite transformaciones affine (lineales), su matriz de transformación se define como una matriz de 3 a 2, omitiendo la tercera columna de la matriz de transformación anterior. En la tabla siguiente se muestra el diseño de la matriz de transformación Direct2D.

   
M11Default: 1.0 M12Default: 0.0
M21Default: 0.0 M22Default: 1.0
M31OffsetX: 0.0 M32OffsetY: 0.0

 

En Direct2D, esta matriz de 3 a 2 se representa mediante la estructura D2D1_MATRIX_3X2 . Para simplificar las operaciones comunes de matriz, Direct2D también proporciona una clase denominada Matrix3x2F, que se deriva de la estructura de D2D1_MATRIX_3X2 .

El constructor predeterminado de Matrix3x2F deja el objeto sin inicializar. Para recuperar una matriz de identidades, use Matrix3x2F::Identity.

Cuando se aplica una transformación de identidad a un objeto, no cambia la posición, la forma ni el tamaño del objeto. Es similar a la forma en que multiplicar un número por 1 no cambia el número. En otras palabras, la transformación de identidad deja solo las coordenadas de los puntos y no desplaza los puntos a una nueva posición. Cualquier transformación distinta de la transformación de identidad modificará la posición, la forma o el tamaño de los objetos.

Las transformaciones se refieren a las coordenadas y la comprensión del espacio de coordenadas de Direct2D es importante para comprender el uso de transformaciones.

Espacio de coordenadas de Direct2D

Direct2D usa un espacio de coordenadas izquierdo; es decir, los valores positivos del eje X aumentan a la derecha y los valores positivos del eje Y aumentan hacia abajo. Todo en la pantalla se coloca en relación con el origen, que es el punto en el que el eje X y el eje Y se intersecan (0, 0), como se muestra en la ilustración siguiente. Los destinos de representación de Direct2D usan este espacio de coordenadas.

ilustración del eje X y del eje Y de un espacio de coordenadas a la izquierda

Mediante la manipulación de valores en una matriz de transformación, puede girar, escalar, asimetría y mover (traducir) un objeto. Por ejemplo, si establece OffsetX en 100 y OffsetY en 200, mueve el objeto a la derecha de 100 píxeles y 200 píxeles hacia abajo.

Para mostrar el efecto del movimiento del objeto, debe aplicar la transformación de traducción para representar destinos, pinceles o geometrías. La aplicación de una transformación para representar destinos afecta a toda la pantalla, mientras que la aplicación de una transformación a un pincel o una geometría solo afecta a ese pincel o geometría específicos. Para crear una matriz de transformación, use la clase Matrix3x2F .

Creación de matrices de transformación

Para crear transformaciones de rotación, escala, asimetría y traducción, la clase Matrix3x2F proporciona los métodos estáticos que se muestran en la tabla siguiente. La columna Ejemplo de la tabla contiene vínculos a los temas de procedimientos que muestran cómo usar cada método de transformación.

Método Descripción Ejemplo Ilustración
matrix3x2f::rotate crea una transformación de rotación que tiene el ángulo y el punto central especificados. cómo rotar un objeto ilustración de un cuadrado girado de 45 grados en el sentido de las agujas del reloj sobre el centro del cuadrado original
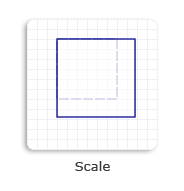
matrix3x2f::scale crea una transformación de escala que tiene los factores de escala y el punto central especificados. escalado de un objeto ilustración de un cuadrado escalado del 130 %
matrix3x2f::skew crea una transformación de asimetría que tiene los valores de eje x e y y especificados y el punto central. cómo sesgar un objeto ilustración de una asimetría cuadrada de 30 grados en sentido contrario a las agujas del reloj desde el eje Y
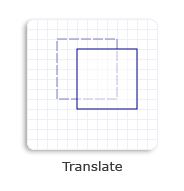
matrix3x2f::translation crea una transformación de traducción y especifica los desplazamientos en la dirección del eje X y del eje Y. cómo traducir un objeto ilustración de un cuadrado movido 20 unidades a lo largo del eje X positivo y 10 unidades a lo largo del eje Y positivo

 

Transformaciones de destino de representación

Un destino de representación es un recurso que hereda de la interfaz ID2D1RenderTarget . Crea recursos para dibujar y realiza operaciones de dibujo reales. También proporciona métodos para transformar el espacio de coordenadas. Puede llamar al método ID2D1RenderTarget::SetTransform para aplicar la transformación especificada al destino de representación. Todas las operaciones de dibujo posteriores se producen en el espacio transformado.

Para representar contenido, use los métodos de dibujo del destino de representación. Antes de empezar a dibujar, llame al método BeginDraw . Para finalizar la representación del contenido, llame al método EndDraw . Para obtener un ejemplo, vea Cómo aplicar varias transformaciones a un objeto.

Transformaciones de pincel

Puede ajustar la transformación en el pincel llamando a SetTransform. Para esta transformación, puede considerar el pincel como una gran pieza de papel y de los diferentes primitivos de representación (texto, geometría, rectángulo, etc.) como galerías de símbolos. Cuando ajustas la transformación del pincel, es como si deslizaste el papel grande debajo de la galería de símbolos, sin cambiar la posición de la galería de símbolos. Puede usar esta técnica para hacer que el texto se desvanezca de amarillo a negro en el espacio 3D.

Cuando la transformación de pincel es la transformación de identidad, los pinceles aparecen en el mismo espacio de coordenadas que el destino de representación en el que se dibujan. La transformación de pincel permite a un autor de la llamada modificar cómo se asignan las coordenadas del pincel a este espacio.

El espacio de pincel se especifica de forma diferente en Direct2D que en Windows Presentation Foundation (WPF). En Direct2D, el espacio de pincel no es relativo al objeto que se dibuja, sino que es el sistema de coordenadas actual del destino de representación, transformado por la transformación de pincel, si hay uno. Para que el pincel rellene un objeto tal como se hizo en WPF, debe traducir el origen del espacio del pincel a la esquina superior izquierda del cuadro de límite del objeto y, a continuación, escalar el espacio del pincel para que el icono base rellene el cuadro de límite del objeto.

Para obtener más información sobre las transformaciones de pincel, consulte Información general sobre pinceles de Direct2D.

Transformaciones de geometría

Al escalar, mover, traducir o sesgar geometrías, puede aplicar directamente una transformación a una geometría específica, no a una transformación de destino de representación que afectaría a toda la pantalla. Una transformación de destino de representación generalmente afecta al trazo y al relleno de una geometría. Por el contrario, una transformación de geometría solo afecta al relleno de una geometría, ya que la transformación se aplica a una geometría antes de que se trazos.

Nota

A partir de Windows 8, la transformación del mundo no afecta al trazo si establece el tipo de trazo en D2D1_STROKE_TRANSFORM_TYPE_FIXED o D2D1_STROKE_TRANSFORM_TYPE_HAIRLINE.

 

Puede ajustar la transformación en una geometría llamando a ID2D1Factory::CreateTransformedGeometry para crear un objeto ID2D1TransformedGeometry . Para obtener más información sobre las transformaciones de geometría, consulte Información general sobre geometrías de Direct2D.

Cómo afecta una transformación de destino de representación a los clips

La transformación en un destino de representación afecta a cómo se calcula el rectángulo delimitador de un clip alineado con el eje. Cuando se llama a PushAxisAlignedClip , el parámetro clipRect se transforma mediante la transformación del mundo actual que se establece en el destino de representación. Después de aplicar la transformación al clipRect, se calcula el rectángulo de límite alineado con el eje para clipRect . Para mejorar la eficacia, el contenido se recorta en este rectángulo de límite alineado con el eje y no en el clipRect original que se pasa. En los diagramas siguientes se muestra cómo se aplica una transformación de rotación al destino de representación, el clipRect resultante y un cuadro de límite alineado con el eje calculado.

  1. Supongamos que el rectángulo de la ilustración siguiente es un destino de representación que está alineado con los píxeles de pantalla.

    ilustración de un rectángulo (destino de representación)

  2. Aplique una transformación de rotación al destino de representación. En la ilustración siguiente, el rectángulo negro representa el destino de representación original y el rectángulo discontinuo rojo representa el destino de representación transformado.

    ilustración del rectángulo original y un rectángulo girado (destino de representación transformado)

  3. Después de llamar a PushAxisAlignedClip , la transformación de rotación se aplica a clipRect. En la ilustración siguiente, el rectángulo azul representa el clipRect transformado.

    ilustración de un rectángulo azul más pequeño (cliprect) dentro del rectángulo girado (destino de representación transformado)

  4. Se calcula el rectángulo de límite alineado con el eje. En la ilustración siguiente, el rectángulo de guiones verde representa el rectángulo delimitador. Todo el contenido se recorta en este rectángulo de límite alineado con el eje.

    ilustración de un cuadro de límite verde en el rectángulo azul pequeño (cliprect)

Resumen

Direct2D facilita la transformación de objetos bidimensionales con espacios de coordenadas simplificados y clases relacionadas. Mediante el uso de varios tipos de transformaciones, puede traducir, rotar, asimetría y escalar los objetos para lograr muchos efectos visuales impresionantes.

Referencia de Direct2D