Koneoppimismallien tulokset

Tämä artikkeli sisältää tietoja sekaannusmatriiseista, luokitteluongelmista ja koneoppimismallien tarkkuudesta. Tarkoitus on parantaa koneoppimisennusteiden tulosten ymmärtämistä. Kohdeyleisöä ovat insinöörit, analysoijat ja esimiehet, jotka haluavat parantaa tietämystään ja taitojaan datatieteen parissa.

Sekaannusmatriisi

Kun valvottu koneoppimisen ongelma on koulutettu aiempien tietojen joukon avulla, se testataan käyttämällä koulutusprosessin tietoja. Näin voidaan vertailla koulutetun mallin ja todellisten arvojen ennusteita. Sekaannusmatriisin avulla voidaan arvioida, miten onnistunut luokitteluongelma on ja missä se tekee virheitä (eli missä kohdassa tapahtuu sekaannus).

Ajatellaan esimerkiksi, että tavoitteena on ennustaa joidenkin fyysisten määritteiden ja toimintamääritteiden avulla, onko lemmikki koira vai kissa. Jos testitietojoukossa on 30 koiraa ja 20 kissaa, sekaannusmatriisi saattaa muistuttaa alla olevaa kuvaa.

Vihreiden solujen numerot edustavat oikeita ennusteita. Kuten näemme, malli ennusti korkeamman prosenttiosuuden kuin kissoja todella on. Mallin yleinen tarkkuus on helppo laskea. Tässä tapauksessa se on 42 ÷ 50 tai 0,84.

Usean luokan luokittelijat sekaannusmatriisissa

Useimmat sekaannusmatriiseja koskevat keskustelut keskittyvät binaarisiin luokittelijoihin edellä olevan esimerkin mukaisesti. Tämä tapaus on erityistapaus, jossa voidaan ottaa huomioon muut mittarit, kuten herkkyys ja peruutus.

Seuraavaksi tarkastellaan kolme tilaa omaavan talousskenarion luokitteluongelmaa. Malli ennustaa, maksetaanko myyntilasku kerralla, myöhässä vai erittäin paljon myöhässä. Esimerkiksi 100 testilaskun joukosta 50 maksetaan ajallaan, 35 myöhässä ja 15 erittäin paljon myöhässä. Tässä tapauksessa malli voi muodostaa sekaannusmatriisin, joka muistuttaa seuraavaa kuvaa.

]

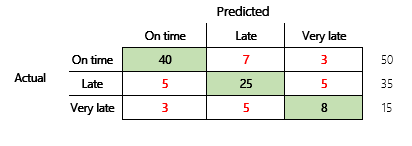Sekaannusmalli sisältää paljon enemmän tietoja kuin yksinkertainen tarkkuusmittari. Siitä huolimatta matriisi on suhteellisen helposti ymmärrettävä. Sekaannusmatriisi kertoo, onko tietojoukko tasapainossa ja ovatko tulostusluokkien määrät samat. Moniluokkainen skenaario kertoo, miten kaukana ennuste voi olla, kun tulostusluokat ovat ordinaaleja, kuten edellä olevassa asiakasmaksuesimerkissä.

Mallin tarkkuus

Eri tarkkuusmittareiden etu on mallin laadun kvantifioiminen.

Koska tarkkuus on helposti ymmärrettävä mittari, se on hyvä aloituskohta esiteltäessä mallia muille henkilöille. Näin erityisesti, jos he eivät ole datatieteilijöitä. Mallin tarkkuuden ymmärtäminen ei edellytä tilastojen ymmärtämistä. Sekaannusmatriisi sisältää lisätietoja mallin suorituskyvystä.

Perinpohjainen ymmärtäminen edellyttää kuitenkin, että tarkkuuteen liittyvät haasteet tulee ottaa huomioon. Mittarin hyödyllisyys riippuu ongelman kontekstista. Mallin suorituskyvyn yhteydessä halutaan usein tietää, miten hyvä malli on. Vastaus tähän kysymykseen ei kuitenkaan välttämättä ole yksinkertainen. Ota huomioon seuraava sekaannusmatriisi (malli 2).

Nopea laskenta osoittaa, että tämän mallin tarkkuus on (70 + 10 + 3) ÷ 100 tai 0,83. Nopeasti ajateltuna näyttää siltä, että tämä on parempi tulos kuin edellisessä usean luokan mallissa (malli 1), jonka tarkkuus on 0,73. Mutta onko tämä parempi?

Ota tämän kysymyksen tarkastelussa huomioon luonnollisen arvauksen tarkkuus. Luokitteluongelmassa yksinkertainen arvaus ennustaa aina yleisimmän luokan. Mallissa 1 tämä arvaus on "ajoissa". Se tuottaa tarkkuudeksi 0,50. Mallissa 2 tämä arvaus on myös "ajoissa". Se tuottaa tarkkuudeksi 0,80. Koska malli 1 parantaa luonnollista arvausta arvolla 0,73 – 0,50 = 0,23 ja malli 2 arvolla 0,83 – 0,80 = 0,03, malli 1 on näistä parempi, vaikka sen tarkkuus on alhaisempi. Laskelma paljastaa, että mallin laadun tehokas arviointi edellyttää tarkkuusarvoa enemmän tietoja.

Toinen näkökulma tulee ottaa huomioon. Ota huomioon skenaario, jossa potilaan sairauden havaitsemisessa käytetään lääketieteellistä testiä. Tämä ongelma on binaarinen luokitteluongelma, jossa positiivinen tulos osoittaa, että potilaalla on kyseinen sairaus. Tässä skenaariossa on otettava huomioon seuraavien virheiden vaikutus:

• Virheelliset positiiviset, joissa testi osoittaa potilaan olevan sairas, mutta oikeasti hän ei ole sairas.
• Virheelliset negatiiviset, joissa testi osoittaa, että potilas ei ole sairas, vaikka tämä oikeasti on.

On selvää, että kumpikaan tapaus ei ole toivottu tulos, mutta kumpi on pahempi? Tämä riippuu tilanteesta. Jos kysymyksessä on henkeä uhkaava sairaus, joka edellyttää nopeaa hoitoa, virheellisten negatiivisten minimoiminen (toivottavasti lisätestien jälkeen) on tärkeintä. Muissa vähemmän kriittisissä tilanteissa mallien tekijät voivat minimoida virheelliset positiiviset sen sijaan. Joka tapauksessa on perusteltua sanoa, että mallin laadun määrittäminen tehokkaasti edellyttää, että tietoja on tarkkuusmittaria enemmän.

Suositukset

Tarkkuus on tärkeä työkalu kommunikoitaessa domain-asiantuntijoiden kanssa, jotka eivät tunne tilastoja. Jotta tiedoista on hyötyä, on tärkeää antaa lisätietoja tarkkuuden arvon kanssa.

Maksuennusteskenaariossa koneoppimismallille voidaan asettaa tavoite, joka sisältää eri maksutoiminnan tekijöitä. Tavoite on, että mallin tulisi parantaa luonnollista arvausta vähentämällä virheellisten vastausten määrää vähintään 50 prosentilla. Toisin sanoen halutaan, että kohdetavoite jakaa eron luonnollisen arvauksen ja 100 prosentin välillä.

Seuraavassa taulukossa on yhteenveto tämän artikkelin sekaannusmatriisien periaatteesta.

Malli	Luonnollinen arvaus	Kohde	Mallin tarkkuus	Onko tavoite täyttynyt?
Malli 1	0.50	0.75	0.73	Lähes. Tämä malli parantaa arvauksia huomattavasti.
Malli 2	0.80	0.90	0.83	Nro Parannus on tarpeen.

Luokituksen F1-tarkkuus

Tässä artikkelissa käsitellään luokituksen koneoppimisen suorituskyvyn lisämittaria, joka on nyt nimeltään F1-tarkkuus.

Ennen kuin F1-tarkkuus voidaan määrittää, on otettava käyttöön kaksi lisämittaria: tarkkuus ja saanti. Tarkkuus ilmaisee, kuinka monta positiiviseksi määritettyä ennustetta on määritetty oikein. Tätä mittaria kutsutaan myös positiiviseksi ennakoivaksi arvoksi. Saanti on niiden todellisten positiivisten tapausten määrä, jotka ennustettiin oikein. Tätä mittaria kutsutaan myös herkkyydeksi.

Edellä olevan kuvan sekaannusmatriisissa nämä mittarit lasketaan seuraavalla tavalla:

• Tarkkuus = TP ÷ (TP + FP)
• Saanti = TP ÷ (TP + FN)

F1-mittari yhdistää tarkkuuden ja saannin. Tuloksena on kahden arvon harmoninen keskiarvo. Se lasketaan seuraavalla tavalla:

• F1 = 2 × (tarkkuus × saanti) ÷ (tarkkuus + saanti)

Alla on konkreettinen esimerkki. Aiemmin tässä artikkelissa oli esimerkki, jossa ennustettiin eläin koiraksi tai kissaksi. Kuva näytetään myös tässä.

Tässä ovat tulokset, jos koira on positiivinen vastaus.

• Tarkkuus = 24 ÷ (24 + 2) = 0,9231
• Saanti = 24 ÷ (24 + 6) = 0,8
• F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572

Kuten nähdään, F1-arvo on tarkkuuden ja saannin välissä.

Vaikka F1-tarkkuuden ymmärtäminen ei ole helppoa, se tuo lisäarvoa tarkkuuden perusarvoon. Se voi myös auttaa epätasapainossa olevien tietojoukkojen käsittelemisessä seuraavan keskustelun tapaan.

Tämän artikkelin Mallin tarkkuus -osassa vertailtiin seuraavaa kahta sekaannusmatriisia. Vaikka ensimmäisen mallin tarkkuus on toista alhaisempi, se arvotettiin hyödyllisemmäksi malliksi, koska se näytti enemmän parannuksia kuin ajallaan tehdyn maksun oletusarvaus.

Katsotaan, miten näitä kahta mallia verrataan, kun käytetään F1-pisteitä. F1-pisteitä käytetään kunkin tilan tarkkuudessa ja saannissa. F1-makrolaskelma määrittää F1-pisteiden keskiarvot tiloissa, jotta saadaan selville yleiset F1-pisteet. F1-muuttujia on muitakin, mutta makroversioon keskittyminen on kiinnostavinta, koska kaikkia kolmea tilaa käsitellään yhtä paljon.

Laskelmien yksinkertaistamiseksi on luotu mallitaulukoita, jotka vastaavat todellisia ja ennustettuja arvoja. Näissä taulukoissa käytettiin Pythonin sklearn-mittarikirjastoa arvojen laskemisessa. Tulos näyttää tältä.

Malli	Luonnollinen arvaus	Tarkkuus	F1-makro
Malli 1	0.5	0.73	0.67
Malli 2	0.80	0.83	0.66

Lisätietoja tämän laskelman toiminnasta on tässä mallin 1 sklearn-mittareiden luokitteluraportissa. Nämä kolme tilaa (Ajoissa, Myöhässä ja Erittäin paljon myöhässä) kuvataan riveillä 1, 2 ja 3. Makron keskiarvo on f1-pisteet-sarakkeen keskiarvo.

	tarkkuus	saanti	f1-pisteet
1	0.83	0.80	0.82
2	0.68	0.71	0.69
3	0.50	0.50	0.50

Näiden kahden mallin F1-makron tarkkuuspisteet ovat lähes samat, kuten tuloksista nähdään. Tässä ja useassa muussa tapauksessa F1-tarkkuus on muita osoittimia parempi mallin ominaisuuden osoitin. Tulosten tulkinta tarkkuuden osalta edellyttää, että käyttäjä ymmärtää mallin tärkeimmät ominaisuudet.