Binaariluokitus

Valmis

Huomautus

Katso lisätietoja Teksti ja kuvat -välilehdeltä!

Luokitus, kuten regressio, on valvottu koneoppimistekniikka. ja sen vuoksi noudattaa samaa toistuvaa mallien koulutus-, validointi- ja arviointiprosessia. Regressiomallin kaltaisten numeeristen arvojen laskemisen sijaan luokitusmallien kouluttamiseen käytettävät algoritmit laskevat luokkamäärityksen todennäköisyysarvot ja arviointimittarit, joita käytetään mallin suorituskyvyn arvioimiseen, vertaavat ennustettuja luokkia todellisiin luokkiin.

Binaariluokitusalgoritmien avulla harjoitetaan malli, joka ennustaa yhden luokan kahdesta mahdollisesta selitteistä. Ennusta käytännössä totuusarvoja tosi tai epätosi. Todellisissa tilanteissa mallin harjoittamiseen ja vahvistamiseen käytetyt tietohavainnot koostuvat useista ominaisuusarvoista (x) ja y-arvosta , joka on joko 1 tai 0.

Esimerkki – binaariluokitus

Jotta voidaan ymmärtää, miten binaariluokitus toimii, tarkastelemme yksinkertaistettua esimerkkiä, jossa käytetään yksittäistä ominaisuutta (x) ennustamaan, onko otsikko 1 vai 0. Tässä esimerkissä käytetään potilaan verensokeria sen ennustamiseen, onko potilaalla diabetes. Tässä ovat tiedot, joilla harjoitamme mallin:

verensokeri (x)	Diabeetikko? (k)
67	0
103	1
114	1
72	0
116	1
65	0

Binaariluokitusmallin harjoittaminen

Mallin harjoittamiseksi käytämme algoritmia, joka sovittaa harjoitustiedot funktioon, joka laskee luokan selitteen todennäköisyydenolevan tosi (toisin sanoen, että potilaalla on diabetes). Todennäköisyys mitataan arvona välillä 0,0–1,0 siten, että kaikkien mahdollisten luokkien kokonaistodennäköisyys on 1,0. Jos esimerkiksi potilaan diabetestodennäköisyys on 0,7, vastaava todennäköisyys on 0,3, ettei potilas ole diabeetinen.

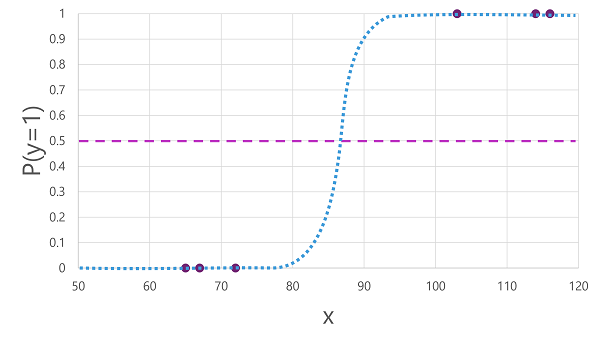
Binaariluokitukseen voidaan käyttää monia algoritmeja, kuten logistinen regressio, joka johtaa sigmoid-funktion (S-muotoinen), jonka arvot ovat välillä 0,0–1,0, kuten tämä:

Huomautus

Nimestään huolimatta koneoppimisen logistista regressiota käytetään luokituksessa, ei regressiossa. Tärkeää on sen tuottaman funktion logistinen luonne, joka kuvaa S-muotoisen käyrän alemman ja ylimmän arvon (0,0 ja 1,0, kun käytetään binaariluokitusta) välillä.

Algoritmin tuottama funktio kuvaa y:n todennäköisyyden olevan tosi (y=1) tietylle x-arvolle. Matemaattisesti voit ilmaista funktion seuraavasti:

f(x) = P(y=1 | x)

Koulutustietojen kuudesta havainnoista kolmelle tiedämme, että y on ehdottomasti tosi, joten todennäköisyys näille havainnoille , että y= 1 on 1,0 , ja kolmelle muulle tiedämme, että y on ehdottomasti epätosi, joten todennäköisyys, että y= 1 on 0,0. S-muotoinen käyrä kuvaa todennäköisyyden jakauman niin, että arvon x piirtäminen riville tunnistaa vastaavan todennäköisyyden sille, että y on 1.

Kaavio sisältää myös vaakasuuntaisen viivan, joka ilmaisee raja-arvon , jonka kohdalla tähän funktioon perustuva malli ennustaa arvon tosi (1) tai epätosi (0). Raja-arvo on y :n keskellä (P(y) = 0,5). Malli ennustaa arvon tosi (1) tämän tai korkeamman arvon osalta. vaikka tämän kohdan alapuolella olevia arvoja käytettäessä se ennustaa false (0). Esimerkiksi potilaan, jonka verensokeri on 90, funktion todennäköisyysarvo olisi 0,9. Koska 0,9 on korkeampi kuin raja-arvo 0,5, malli ennustaa arvoa tosi (1) - toisin sanoen potilaalla ennustetaan olevan diabetes.

Binaariluokitusmallin arviointi

Regression tavoin binaariluokitusmallia harjoittaessasi pidät painettuna satunnaista tietojen alijoukkoa, jonka avulla harjoitettu malli vahvistetaan. Oletetaan, että pidättelimme seuraavia tietoja diabetesluokituksen vahvistamiseksi:

verensokeri (x)	Diabeetikko? (k)
66	0
107	1
112	1
71	0
87	1
89	1

Käyttämällä aiemmin x-arvoihin johdettua logistista funktiota tuloksena on seuraava piirto.

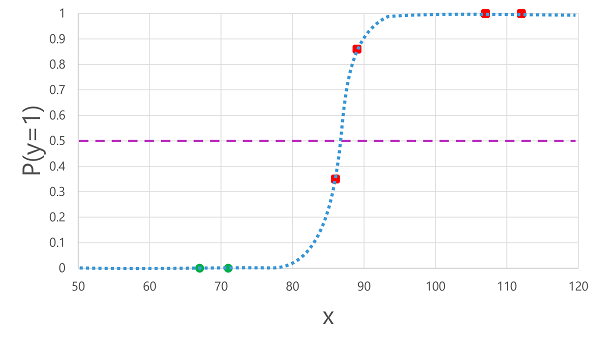
Sen perusteella, onko funktion laskema todennäköisyys raja-arvon ylä- vai alapuolella, malli luo kullekin havainnolle ennustetun otsikon 1 tai 0. Voimme sitten verrata ennustettuja luokkaotsikoita () todellisiin luokkaotsikoihin (y) seuraavassa esitetyllä tavalla:

verensokeri (x)	Todellinen diabetesdiagnoosi (y)	Ennustettu diabetesdiagnoosi ()
66	0	0
107	1	1
112	1	1
71	0	0
87	1	0
89	1	1

Binaariluokituksen arvioinnin mittarit

Ensimmäinen vaihe binaariluokitusmallin arviointitietojen laskennassa on yleensä luoda matriisi, jossa on oikeat ja virheelliset ennusteet kullekin mahdolliselle luokkaotsikolle:

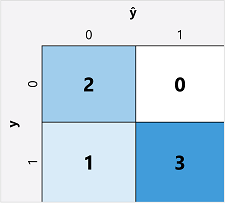
Tätä visualisointia kutsutaan sekaannusmatriisiksi, ja se näyttää ennusteen kokonaissummat, joissa:

• =0 ja y=0: True-negatiiviset (TN)
• =1 ja y=0: False-positiiviset (FP)
• =0 ja y=1: False-negatiiviset (FN)
• =1 ja y=1: True-positiiviset (TP)

Sekaannusmatriisin järjestely on sellainen, että oikeat (tosi) ennusteet näytetään lävistäjällä vasemmalta alaoikealle. Usein väri-intensiteettiä käytetään ilmaisemaan ennusteiden määrä kussakin solussa, joten nopealla silmäyksellä malliin, joka ennustaa hyvää, pitäisi paljastaa syvälle varjostettu lävistäjän trendi.

Tarkkuus

Yksinkertaisin arvo, jonka voit laskea sekaannusmatriisista, on tarkkuus – mallin oikeiden ennusteiden osuus. Tarkkuus lasketaan seuraavasti:

(TN+ TP) ÷ (TN + FN + FP + TP)

Diabetesesimerkin kohdalla laskutoimitus on:

(2+3) ÷ (2+1+0+3)

= 5 ÷ 6

= 0.83

Diabetesluokitusmalli tuotti validointitiedoillamme oikeat ennusteet 83% ajan.

Tarkkuus voi aluksi tuntua hyvältä mittarilta mallin arvioimiseksi, mutta harkitse tätä. Oletetaan, että 11% väestöllä on diabetes. Voit luoda mallin, joka ennustaa aina 0, ja sen tarkkuus olisi 89%, vaikka sillä ei ole todellista yritystä erottaa potilaita niiden ominaisuuksien arvioinnin avulla. Tarvitsemme syvempää ymmärrystä siitä, miten malli suoriutuu ennustamaan 1 positiivisissa tapauksissa ja 0 negatiivisissa tapauksissa.

Muistaa

Recall on mittari, joka mittaa mallin tunnistamien positiivisten tapausten osuuden oikein. Toisin sanoen, verrattuna niiden potilaiden määrään, joilla on diabetes, kuinka monta malli ennusti diabetekseen?

Paikannuskaava on seuraava:

TP ÷ (TP + FN)

Esimerkki diabeteksesta:

3 ÷ (3+1)

= 3 ÷ 4

= 0.75

Niinpä mallimme tunnisti oikein 75% potilaista, joilla on diabetes.

Tarkkuus

Tarkkuus on samanlainen mittausarvo kuin paikannus, mutta mittaa niiden positiivisten tapausten osuuden, joissa tosi-otsikko on todellisuudessa positiivinen. Toisin sanoen, mikä osuus mallin ennustamista potilaista on diabetes?

Tarkkuuden kaava on seuraava:

TP ÷ (TP + FP)

Esimerkki diabeteksesta:

3 ÷ (3+0)

= 3 ÷ 3

= 1.0

Niinpä 100% potilaista, joiden mallimme on ennustanut olevan diabetes, on itse asiassa diabetes.

F1-pisteet

F1-pistemäärä on yleinen mittausarvo, joka yhdistää paikannukset ja tarkkuuden. F1-pistemäärän kaava on seuraava:

(2 x tarkkuus x paikannus) ÷ (Tarkkuus + paikannus)

Esimerkki diabeteksesta:

(2 x 1,0 x 0,75) ÷ (1,0 + 0,75)

= 1,5 ÷ 1,75

= 0,86

Käyrän alla oleva alue (AUC)

Toinen paikannuksen nimi on true-positiivinen korko (TPR), ja käytössä on vastaava mittausarvo, jota kutsutaan false-positiiviseksi prosenttimääräksi (FPR), joka lasketaan kaavalla FP÷(FP+ TN). Tiedämme jo, että mallin TPR-arvo 0,5:n raja-arvoa käytettäessä on 0,75, ja voimme laskea FPR-kaavan avulla arvon 0÷2 = 0.

Jos luonnollisesti muutamme kynnysarvoa, jonka yläpuolelle malli ennustaa arvon tosi (1), se vaikuttaisi positiivisten ja negatiivisten ennusteiden määrään. ja siksi muuttaa TPR- ja FPR-mittareita. Näitä mittareita käytetään usein mallin arvioimiseen piirtämällä vastaanotetun operaattorin ominaisuuden (ROC) käyrä, joka vertaa TPR:ää ja FPR:ää jokaiseen mahdolliseen raja-arvoon välillä 0,0–1,0:

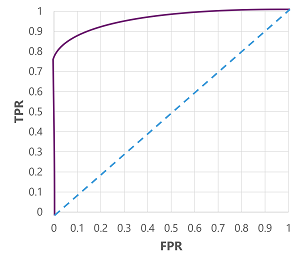
Täydellisen mallin ROC-käyrä menisi suoraan vasemmalla olevalle TPR-akselille ja sitten ylimmälle FPR-akselille. Koska käyrän piirtoalue mittaa 1x1, tämän täydellisen käyrän alla oleva alue olisi 1,0 (eli malli on oikea 100% ajan). Sen sijaan vinoviiva vasemmasta alakulmasta oikeaan yläkulmaan edustaa tuloksia, jotka saavutettaisiin satunnaisarvaamalla binaariotsikko. tuottamalla 0,5-käyrän alla olevan alueen. Toisin sanoen, kun annetaan kaksi mahdollista luokkatunnistetta, voit kohtuullisesti odottaa arvailevasi oikein 50% ajan.

Diabetesmallin tapauksessa tuotetaan yllä oleva käyrä ja käyrän alla oleva alue (AUC) mittari on 0,875. Koska AUC on suurempi kuin 0,5, voimme päätellä, että malli toimii paremmin ennustamaan, onko potilaalla diabetes vai ei, kuin satunnaisesti arvailemalla.