Théorie de l’algorithme de recherche de Grover
Dans cet article, vous trouverez une explication théorique détaillée des principes mathématiques qui décrivent le fonctionnement de l’algorithme de Grover.
Pour une implémentation pratique de l’algorithme de Grover pour résoudre les problèmes mathématiques, consultez l’algorithme de recherche de Grover.
Énoncé du problème
L’algorithme de Grover accélère la solution aux recherches de données non structurées (ou problème de recherche), en exécutant la recherche en moins d’étapes que n’importe quel algorithme classique. Toute tâche de recherche peut être exprimée à l’aide d’une fonction abstraite $f(x)$ qui accepte des éléments de recherche $x$. Si l’élément $x$ est une solution à la tâche de recherche, alors $f(x)=1$. Si l’élément $x$ n’est pas une solution, alors $f(x)=0$. Le problème de recherche consiste à trouver tout élément $x_0$ tel que $f(x_0)=1$.
En effet, tout problème qui vous permet de vérifier si une valeur $donnée x$ est une solution valide (un &guillemet ; Oui ou aucun guillemet de problème& ;) peut être formulé en termes de problème de recherche. Voici quelques exemples :
- Problème de satisfiabilité booléenne : l’ensemble de valeurs $booléennes x$ une interprétation (une affectation de valeurs à des variables) qui satisfait à la formule booléenne donnée ?
- Problème des vendeurs itinérants : X$ décrit-t-il $la boucle la plus courte possible qui connecte toutes les villes ?
- Problème de recherche de base de données : la table de base de données contient-elle un enregistrement $x$ ?
- Problème de factorisation d’entier : le nombre $fixe N$ divise-t-il par le nombre $x$ ?
La tâche que l’algorithme de Grover vise à résoudre peut être exprimée comme suit : étant donné une fonction classique $f(x):{0,1}^n \rightarrow\{0,1\}$, où $n$ est la taille de l’espace de recherche, recherchez une entrée $x_0$ pour laquelle $f(x_0)=1$. La complexité de l’algorithme est mesurée par le nombre d’utilisations de la fonction $f(x)$. Traditionnellement, dans le pire des cas, nous devons évaluer $f(x)$ un total de $n-1$ fois, où $N=2^n$, en essayant toutes les possibilités. Après $N-1$ éléments, il doit s’agir du dernier élément. L’algorithme quantique de Grover peut résoudre ce problème beaucoup plus rapidement, en offrant une accélération quadratique. Quadratique ici implique que seules $\sqrt{ évaluations N}$ environ sont requises, par rapport à $N$.
Structure de l’algorithme
Supposons que nous avons $N=2^n$ éléments éligibles pour la tâche de recherche et que nous les indexons en affectant à chaque élément un entier compris entre $0$ et $N-1$. Par ailleurs, supposons qu’il y a $M$ entrées valides différentes, ce qui signifie qu’il y a $M$ entrées pour lesquelles $f(x)=1$. Les étapes de l’algorithme sont les suivantes :
- Commencez avec un registre de $n$ qubits initié dans l’état $\ket{0}$.
- Préparez le registre en une superposition uniforme en appliquant $H$ à chaque qubit du registre : $$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
- Appliquez les opérations suivantes au registre $N_{\text{ heures optimales}}$ :
- La phase Oracle $O_f$ qui applique un décalage de phase conditionnel de $-1$ pour les éléments de la solution.
- Appliquez $H$ à chaque qubit dans le registre.
- Un décalage de phase conditionnel de $-1$ à chaque état de base de calcul, sauf $\ket{0}$. Cela peut être représenté par l’opération unitaire $-O_0$, car $O_0$ représente le décalage de phase conditionnel sur $\ket{0}$ uniquement.
- Appliquez $H$ à chaque qubit dans le registre.
- Mesurez le registre pour obtenir l’index d’un élément qui est une solution avec une très grande probabilité.
- Vérifier s’il s’agit d’une solution valide. Si ce n’est pas le cas, recommencer.
$N_\text{optimal}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{{2}\right\rfloor$ est le nombre optimal d’itérations qui optimise la probabilité d’obtention de l’élément correct en mesurant le registre.
Remarque
L’application conjointe des étapes 3.b, 3.c et 3.d est généralement connue dans la littérature comme opérateur de diffusion de Grover.
L’opération d’unité globale appliquée au registre est la suivante :
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$
Suivre l’état du registre, étape par étape
Pour illustrer le processus, nous allons suivre les transformations mathématiques de l’état du registre pour un cas simple dans lequel il y a uniquement deux qubits et où l’élément valide est $\ket{01}.$
Le registre commence à l’état : $$|\text{register}\rangle=|00\rangle$$
Après l’application de $H$ à chaque qubit, l’état du registre se transforme en : $$|\text{register}\rangle=\frac{{1}{\sqrt{{4}}\sum_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$
La phase d’oracle est ensuite appliquée pour obtenir : $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$
Ensuite, $H$ agit à nouveau sur chaque qubit pour donner : $$|\text{register}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$
À présent, le décalage de phase conditionnel est appliqué à chaque état sauf $\ket{00}$ : $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$
Enfin, nous terminons la première itération Grover en appliquant $H$ à nouveau pour obtenir : $$|\text{register}\rangle=\ket{{01}$$
En suivant les étapes ci-dessus, l’élément valide est trouvé en une seule itération. Comme vous le verrez plus tard, c’est parce que pour N=4 et un seul élément valide, $N_\text{optimal}=1$.
Explication géométrique
Pour comprendre le fonctionnement de l’algorithme de Grover, nous allons étudier l’algorithme d’un point de vue géométrique. Nommons $\ket{\text{}}$ la superposition de tous les états qui ne constituent pas une solution au problème de recherche. En supposant qu’il y a $M$ solutions valides :
$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
L’état $\ket{\text{good}}$ est défini comme la superposition de tous les états qui sont une solution au problème de recherche :
$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
Comme good et bad sont des jeux mutuellement exclusifs, car un élément ne peut pas être valide et non valide, les états $\ket{\text{}}$et$\ket{\text{}}$sont orthogonaux. Les deux états forment la base orthogonale d’un plan dans l’espace de vectoriel. Nous pouvons utiliser ce plan pour visualiser l’algorithme.
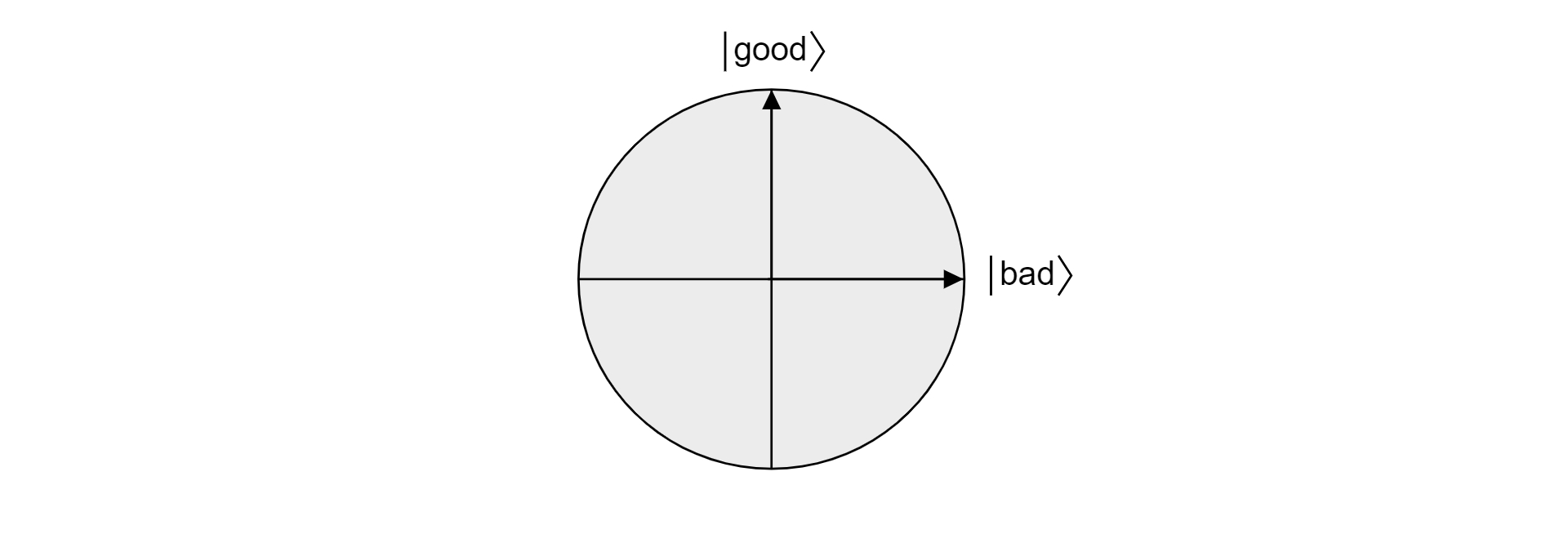
Prenons maintenant $\ket{\psi}$, un état arbitraire qui réside dans le plan couvert par $\ket{\text{good}}$ et $\ket{\text{bad}}$. Tout état vivant dans ce plan peut être exprimé comme suit :
$$\ket{\psi}=\alpha\ket{\text{good}} + \beta\ket{\text{bad}}$$
où $\alpha$ et $\beta$ sont des nombres réels. À présent, nous allons introduire l’opérateur de réflexion $R_{\ket{\psi}}$, où $\ket{\psi}$ est tout état qubit vivant dans le plan. L’opérateur est défini ainsi :
$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$
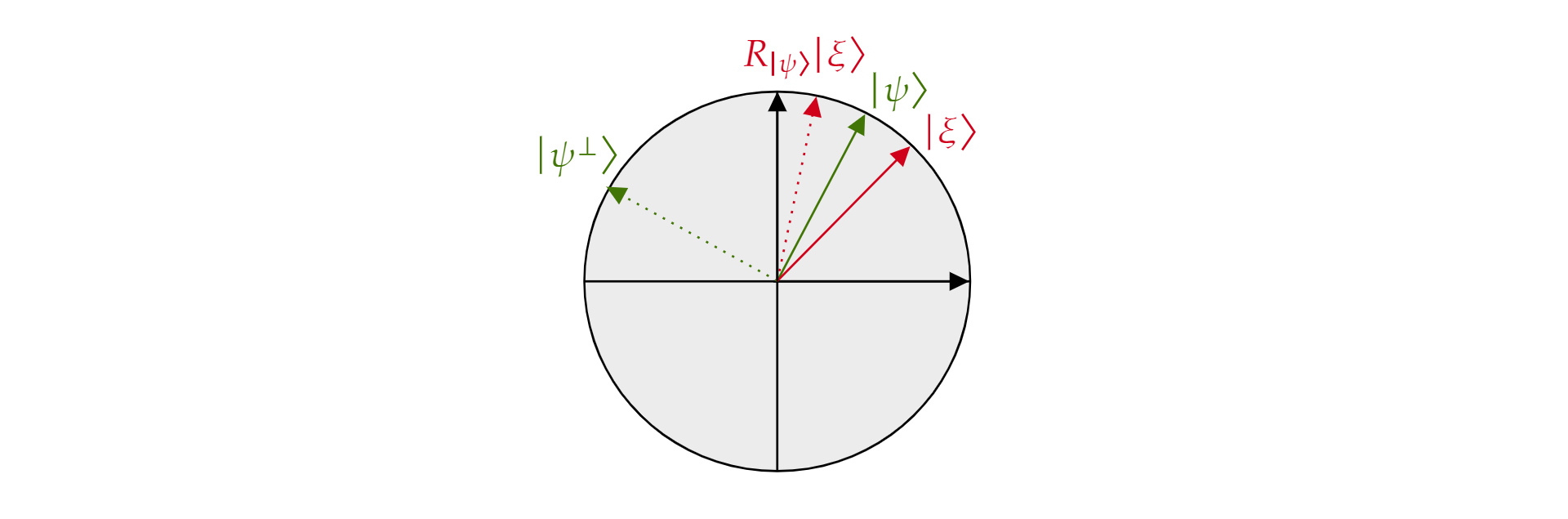
On parle d’opérateur de réflexion sur $\ket{\psi}$, car il peut être interprété géométriquement comme une réflexion sur la direction de $\ket{\psi}$. Pour le voir, prenez la base orthogonale du plan formé par $\ket{\psi}$ et son complément orthogonal $\ket{\psi^{\perp}}$. Tous état $\ket{\xi}$ du plan peut être décomposé de la manière suivante :
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
Si l’opérateur $R_{\ket{\psi}}$ est appliqué à $\ket{\xi}$ :
$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
L’opérateur $R_\ket{\psi}$ inverse le composant orthogonal à $\ket{\psi}$, mais laisse le composant $\ket{\psi}$ inchangé. Par conséquent, $R_\ket{\psi}$ est une réflexion sur $\ket{\psi}$.
L’algorithme de Grover, après la première application de $H$ à chaque qubit, commence par une superposition uniforme de tous les états. Cela peut être écrit comme suit :
$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$
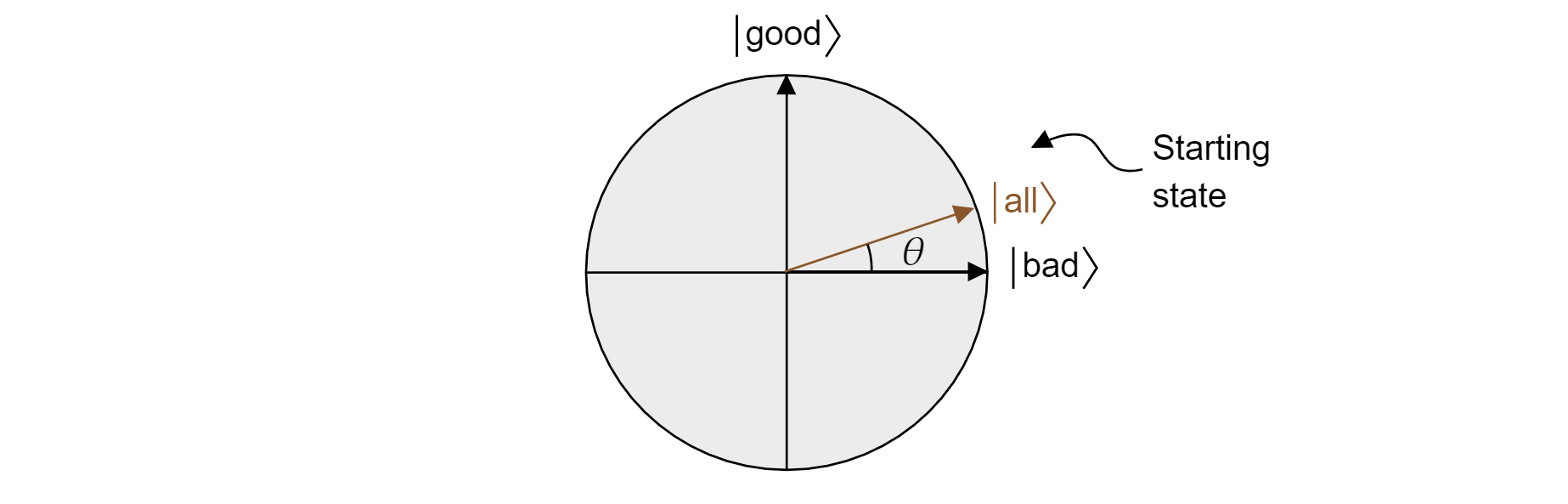
Par conséquent, l’état vit dans le plan. Notez que la probabilité d’obtenir un résultat correct lors de la mesure à partir de la superposition égale est juste bonne}|{\text{toutes$|\braket{\text{^}}}|2=M/N$, c’est-à-dire ce que vous attendez d’une estimation aléatoire.
L’oracle $O_f$ ajoute une phase négative à toute solution au problème de recherche. Par conséquent, il peut être écrit comme une réflexion sur l’axe $\ket{\text{bad}}$ :
$$O_f = R_{\ket{\text{bad}}}= 2\ket{\text{bad}}\bra{\text{bad}} - \mathcal{I}$$
De même, le changement de phase conditionnelle $O_0$ est simplement une réflexion inversée sur l’état $\ket{0}$ :
$$O_0 = R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I}$$
En connaissant ce fait, il est facile de vérifier que l’opération de diffusion de Grover $-H^{\otimes n} O_0 H^{\otimes n}$ est également une réflexion sur l’état $\ket{all}$. Il suffit d’effectuer :
$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{all}} - \mathcal{I}= R_{\ket{\text{all}}}$$
Nous venons de démontrer que chaque itération de l’algorithme de Grover est une composition de deux réflexions, $R_\ket{\text{bad}}$ et $R_\ket{\text{all}}$.
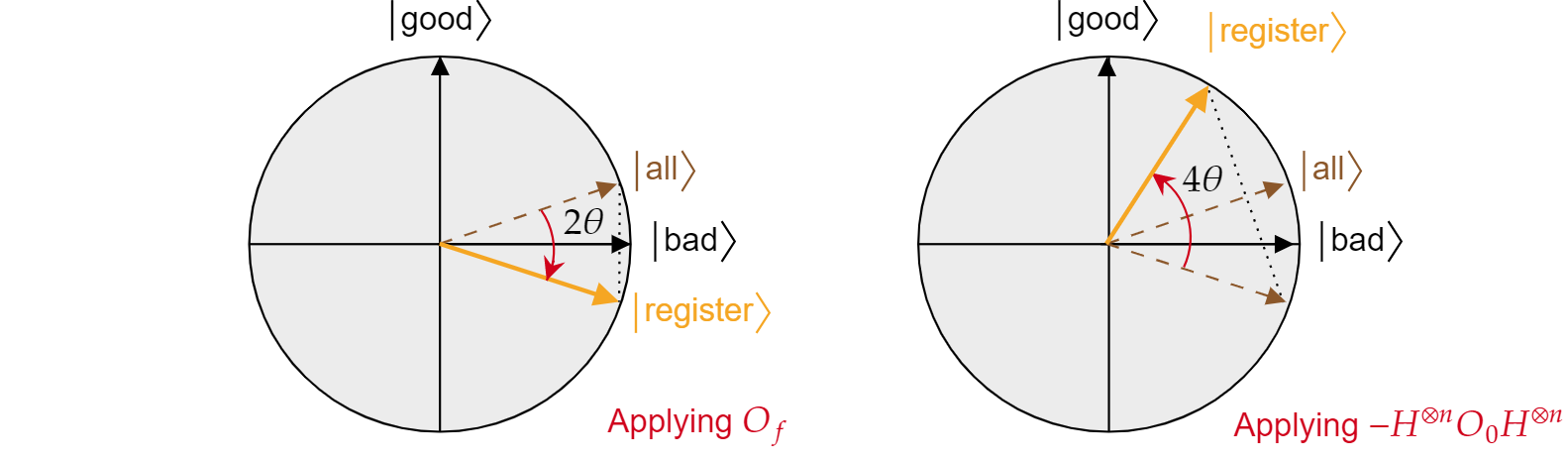
L’effet combiné de chaque itération de Grover est une rotation dans le sens horaire inverse d’un angle $2\theta$. Heureusement, l’angle $\theta $ est facile à trouver. Étant donné que $\theta$ est juste l’angle entre $\ket{\text{all}}$ et $\ket{\text{bad}}$, nous pouvons utiliser le produit scalaire pour trouver l’angle. Nous savons que $\cos{\theta}=\braket{\text{all}|\text{bad}}$, donc nous devons calculer $\braket{\text{all}|\text{bad}}$. De la décomposition de $\ket{\text{all}}$ en $\ket{\text{bad}}$ et $\ket{\text{good}}$, nous obtenons ceci :
$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
L’angle entre l’état du registre et le $\ket{\text{bon}}$ état diminue avec chaque itération, ce qui entraîne une probabilité plus élevée de mesurer un résultat valide. Pour calculer cette probabilité, vous devez simplement calculer $|\braket{\text{le bon}|\text{registre}}|^2$. En indiquant l’angle entre $\ket{\text{good}}$ et $\ket{\text{register}}$$\gamma (k)$, où $k$ est le nombre d’itérations :
$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$
Par conséquent, la probabilité de réussite est :
$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
Nombre optimal d’itérations
Étant donné que la probabilité de réussite peut être écrite en fonction du nombre d’itérations, nous pouvons trouver le nombre optimal d’itérations $N_{\text{optimal}}$ en calculant le plus petit entier positif (approximativement) qui maximise la fonction de probabilité de réussite.
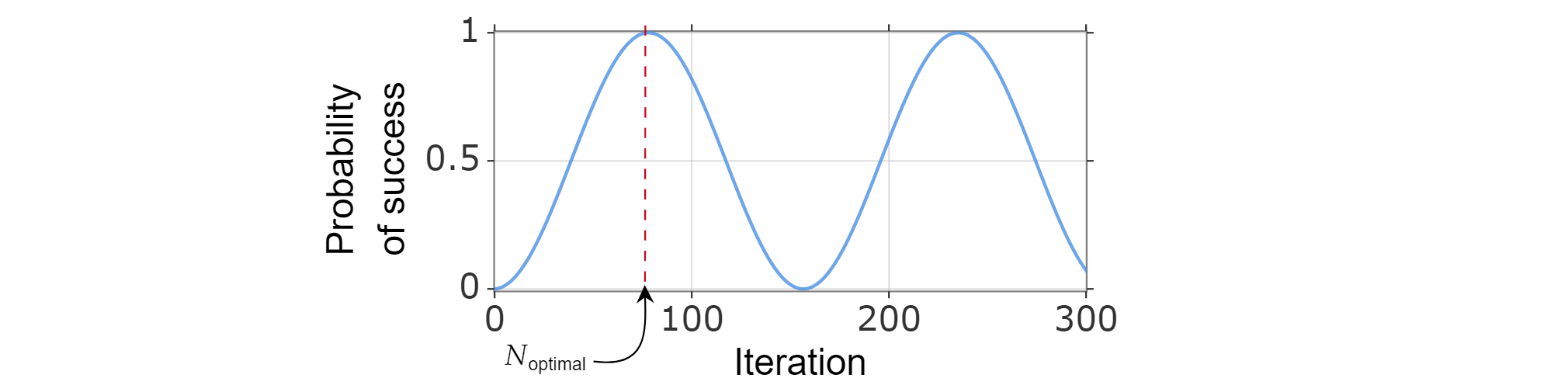
Nous savons que $\sin^2{x}$ atteint sa première valeur maximale pour $x=\frac{\pi}{2}$, donc :
$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$
Cela donne :
$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$
Où, dans la dernière étape, $\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$.
Par conséquent, vous pouvez choisir N_optimal}$ à N_\text{$optimal}=\left\lfloor \frac{\pi{4}\sqrt{\frac{}{N M}}}{-\right\frac{{1}{2}\rfloor.$\text{$
Analyse de complexité
À partir de l’analyse précédente, $O\left(\sqrt{\frac{N}{M}}\right)$ requêtes de l’oracle $O_f$ sont nécessaires pour trouver un élément valide. Toutefois, l’algorithme peut-il être implémenté efficacement en termes de complexité temporelle ? $O_0$ est basé sur le calcul d’opérations booléennes sur $n$ bits et est connu pour être implémenté à l’aide de $O(n)$ portes. Nous avons également deux couches de $n$ portes de Hadarmard. Ces deux composants nécessitent donc uniquement des $O(n)$ portes par itération. Comme $N=2^n$, nous avons $O(n)=O(log(N))$. Par conséquent, si $O\left(\sqrt{\frac{N}{M}}\right)$ itérations et de $O(log(N))$ portes par itération sont nécessaires, la complexité temporelle totale (sans tenir compte de l’implémentation de l’oracle) est $O\left(\sqrt{\frac{N}{M}}log(N)\right)$.
La complexité globale de l’algorithme dépend finalement de la complexité de l’implémentation de l’oracle $O_f$. Si une évaluation de fonction est beaucoup plus compliquée sur un ordinateur quantique que sur un ordinateur classique, le runtime d’algorithme global sera plus long dans le cas quantique, même si techniquement, il utilise moins de requêtes.
Références
Si vous souhaitez poursuivre l’apprentissage de l’algorithme de Grover, vous pouvez consulter les sources suivantes :
- Papier d’origine par Lov K. Grover
- Section Algorithmes de recherche quantique de Nielsen, M. A. &ère; Chuang, I. L. (2010). Informations sur le calcul quantique et le quantum.
- Algorithme de Grover sur Arxiv.org