Différentes façons d’exécuter l’estimateur de ressources

Dans cet article, vous allez apprendre à utiliser l’estimateur de ressources Azure Quantum. L’estimateur de ressources fait partie du Kit de développement Quantum et est disponible dans différentes plateformes et IDE.

Si vous exécutez un programme Q#, l’estimateur de ressources est disponible dans Visual Studio Code avec l’extension Quantum Development Kit. Vous n’avez pas besoin d’un abonnement Azure pour utiliser l’estimateur de ressources dans Visual Studio Code.

Si vous exécutez un programme Qiskit ou QIR, l’estimateur de ressources est disponible dans le Portail Azure et vous avez besoin d’un abonnement Azure pour l’utiliser.

Le tableau suivant montre les différentes façons d’exécuter l’estimateur de ressources.

Scénario utilisateur	Plateforme	Didacticiel
Estimer les ressources d’un programme Q#	Visual Studio Code	Sélectionnez Q# dans VS Code en haut de la page
Estimer les ressources d’un programme Q# (avancé)	Jupyter Notebook dans Visual Studio Code	Sélectionnez Q# dans Jupyter Notebook en haut de la page
Estimer les ressources d’un programme Qiskit	Portail Azure	Sélectionnez Qiskit dans Portail Azure en haut de la page
Estimer les ressources d’un programme QIR	Portail Azure	Envoyer le QIR
Utiliser des fichiers FCIDUMP comme paramètres d’argument (avancé)	Visual Studio Code	Soumettre un problème de chimie quantique

Conditions préalables pour VS Code

• La dernière version de Visual Studio Code ou ouvrir VS Code sur le web.
• La dernière version de l’extension Kit de développement Azure Quantum. Pour plus d’informations sur l’installation, consultez Installation du QDK sur VS Code.

Conseil

Vous n’avez pas besoin d’avoir un compte Azure pour exécuter l’estimateur de ressource local.

Créer un fichier Q#

1. Ouvrez Visual Studio Code et sélectionnez Fichier > Nouveau fichier texte pour créer un fichier.
2. Enregistrez le fichier sous le nom ShorRE.qs. Ce fichier contient le code Q# de votre programme.

Créer l’algorithme quantique

Copiez le code suivant dans le fichier ShorRE.qs :

    import Std.Arrays.*;
    import Std.Canon.*;
    import Std.Convert.*;
    import Std.Diagnostics.*;
    import Std.Math.*;
    import Std.Measurement.*;
    import Microsoft.Quantum.Unstable.Arithmetic.*;
    import Std.ResourceEstimation.*;

    operation Main() : Unit {
        let bitsize = 31;

        // When choosing parameters for `EstimateFrequency`, make sure that
        // generator and modules are not co-prime
        let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
    }

    // In this sample we concentrate on costing the `EstimateFrequency`
    // operation, which is the core quantum operation in Shors algorithm, and
    // we omit the classical pre- and post-processing.

    /// # Summary
    /// Estimates the frequency of a generator
    /// in the residue ring Z mod `modulus`.
    ///
    /// # Input
    /// ## generator
    /// The unsigned integer multiplicative order (period)
    /// of which is being estimated. Must be co-prime to `modulus`.
    /// ## modulus
    /// The modulus which defines the residue ring Z mod `modulus`
    /// in which the multiplicative order of `generator` is being estimated.
    /// ## bitsize
    /// Number of bits needed to represent the modulus.
    ///
    /// # Output
    /// The numerator k of dyadic fraction k/2^bitsPrecision
    /// approximating s/r.
    operation EstimateFrequency(
        generator : Int,
        modulus : Int,
        bitsize : Int
    )
    : Int {
        mutable frequencyEstimate = 0;
        let bitsPrecision =  2 * bitsize + 1;

        // Allocate qubits for the superposition of eigenstates of
        // the oracle that is used in period finding.
        use eigenstateRegister = Qubit[bitsize];

        // Initialize eigenstateRegister to 1, which is a superposition of
        // the eigenstates we are estimating the phases of.
        // We first interpret the register as encoding an unsigned integer
        // in little endian encoding.
        ApplyXorInPlace(1, eigenstateRegister);
        let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);

        // Use phase estimation with a semiclassical Fourier transform to
        // estimate the frequency.
        use c = Qubit();
        for idx in bitsPrecision - 1..-1..0 {
            within {
                H(c);
            } apply {
                // `BeginEstimateCaching` and `EndEstimateCaching` are the operations
                // exposed by Azure Quantum Resource Estimator. These will instruct
                // resource counting such that the if-block will be executed
                // only once, its resources will be cached, and appended in
                // every other iteration.
                if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
                    Controlled oracle([c], (1 <<< idx, eigenstateRegister));
                    EndEstimateCaching();
                }
                R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
            }
            if MResetZ(c) == One {
                set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
            }
        }

        // Return all the qubits used for oracles eigenstate back to 0 state
        // using Microsoft.Quantum.Intrinsic.ResetAll.
        ResetAll(eigenstateRegister);

        return frequencyEstimate;
    }

    /// # Summary
    /// Interprets `target` as encoding unsigned little-endian integer k
    /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
    /// p is `power`, g is `generator` and N is `modulus`.
    ///
    /// # Input
    /// ## generator
    /// The unsigned integer multiplicative order ( period )
    /// of which is being estimated. Must be co-prime to `modulus`.
    /// ## modulus
    /// The modulus which defines the residue ring Z mod `modulus`
    /// in which the multiplicative order of `generator` is being estimated.
    /// ## power
    /// Power of `generator` by which `target` is multiplied.
    /// ## target
    /// Register interpreted as little endian encoded which is multiplied by
    /// given power of the generator. The multiplication is performed modulo
    /// `modulus`.
    internal operation ApplyOrderFindingOracle(
        generator : Int, modulus : Int, power : Int, target : Qubit[]
    )
    : Unit
    is Adj + Ctl {
        // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
        // also use `ExpModI` to compute a by which x must be multiplied. Also
        // note that we interpret target as unsigned integer in little-endian
        // encoding.
        ModularMultiplyByConstant(modulus,
                                    ExpModI(generator, power, modulus),
                                    target);
    }

    /// # Summary
    /// Performs modular in-place multiplication by a classical constant.
    ///
    /// # Description
    /// Given the classical constants `c` and `modulus`, and an input
    /// quantum register  |𝑦⟩, this operation
    /// computes `(c*x) % modulus` into |𝑦⟩.
    ///
    /// # Input
    /// ## modulus
    /// Modulus to use for modular multiplication
    /// ## c
    /// Constant by which to multiply |𝑦⟩
    /// ## y
    /// Quantum register of target
    internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
    : Unit is Adj + Ctl {
        use qs = Qubit[Length(y)];
        for (idx, yq) in Enumerated(y) {
            let shiftedC = (c <<< idx) % modulus;
            Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
        }
        ApplyToEachCA(SWAP, Zipped(y, qs));
        let invC = InverseModI(c, modulus);
        for (idx, yq) in Enumerated(y) {
            let shiftedC = (invC <<< idx) % modulus;
            Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
        }
    }

    /// # Summary
    /// Performs modular in-place addition of a classical constant into a
    /// quantum register.
    ///
    /// # Description
    /// Given the classical constants `c` and `modulus`, and an input
    /// quantum register  |𝑦⟩, this operation
    /// computes `(x+c) % modulus` into |𝑦⟩.
    ///
    /// # Input
    /// ## modulus
    /// Modulus to use for modular addition
    /// ## c
    /// Constant to add to |𝑦⟩
    /// ## y
    /// Quantum register of target
    internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
    : Unit is Adj + Ctl {
        body (...) {
            Controlled ModularAddConstant([], (modulus, c, y));
        }
        controlled (ctrls, ...) {
            // We apply a custom strategy to control this operation instead of
            // letting the compiler create the controlled variant for us in which
            // the `Controlled` functor would be distributed over each operation
            // in the body.
            //
            // Here we can use some scratch memory to save ensure that at most one
            // control qubit is used for costly operations such as `AddConstant`
            // and `CompareGreaterThenOrEqualConstant`.
            if Length(ctrls) >= 2 {
                use control = Qubit();
                within {
                    Controlled X(ctrls, control);
                } apply {
                    Controlled ModularAddConstant([control], (modulus, c, y));
                }
            } else {
                use carry = Qubit();
                Controlled AddConstant(ctrls, (c, y + [carry]));
                Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
                Controlled AddConstant([carry], (modulus, y));
                Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
            }
        }
    }

    /// # Summary
    /// Performs in-place addition of a constant into a quantum register.
    ///
    /// # Description
    /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
    /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
    ///
    /// # Input
    /// ## c
    /// Constant number to add to |𝑦⟩.
    /// ## y
    /// Quantum register of second summand and target; must not be empty.
    internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
        // We are using this version instead of the library version that is based
        // on Fourier angles to show an advantage of sparse simulation in this sample.

        let n = Length(y);
        Fact(n > 0, "Bit width must be at least 1");

        Fact(c >= 0, "constant must not be negative");
        Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");

        if c != 0 {
            // If c has j trailing zeroes than the j least significant bits
            // of y won't be affected by the addition and can therefore be
            // ignored by applying the addition only to the other qubits and
            // shifting c accordingly.
            let j = NTrailingZeroes(c);
            use x = Qubit[n - j];
            within {
                ApplyXorInPlace(c >>> j, x);
            } apply {
                IncByLE(x, y[j...]);
            }
        }
    }

    /// # Summary
    /// Performs greater-than-or-equals comparison to a constant.
    ///
    /// # Description
    /// Toggles output qubit `target` if and only if input register `x`
    /// is greater than or equal to `c`.
    ///
    /// # Input
    /// ## c
    /// Constant value for comparison.
    /// ## x
    /// Quantum register to compare against.
    /// ## target
    /// Target qubit for comparison result.
    ///
    /// # Reference
    /// This construction is described in [Lemma 3, arXiv:2201.10200]
    internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
    : Unit is Adj+Ctl {
        let bitWidth = Length(x);

        if c == 0 {
            X(target);
        } elif c >= 2 ^ bitWidth {
            // do nothing
        } elif c == 2 ^ (bitWidth - 1) {
            ApplyLowTCNOT(Tail(x), target);
        } else {
            // normalize constant
            let l = NTrailingZeroes(c);

            let cNormalized = c >>> l;
            let xNormalized = x[l...];
            let bitWidthNormalized = Length(xNormalized);
            let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));

            use qs = Qubit[bitWidthNormalized - 1];
            let cs1 = [Head(xNormalized)] + Most(qs);
            let cs2 = Rest(xNormalized);

            within {
                for i in IndexRange(gates) {
                    (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
                }
            } apply {
                ApplyLowTCNOT(Tail(qs), target);
            }
        }
    }

    /// # Summary
    /// Internal operation used in the implementation of GreaterThanOrEqualConstant.
    internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
        within {
            ApplyToEachA(X, [control1, control2]);
        } apply {
            ApplyAnd(control1, control2, target);
            X(target);
        }
    }

    internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
    : Unit is Adj {
        body (...) {
            CCNOT(control1, control2, target);
        }
        adjoint (...) {
            H(target);
            if (M(target) == One) {
                X(target);
                CZ(control1, control2);
            }
        }
    }


    /// # Summary
    /// Returns the number of trailing zeroes of a number
    ///
    /// ## Example
    /// ```qsharp
    /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
    /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
    /// ```
    internal function NTrailingZeroes(number : Int) : Int {
        mutable nZeroes = 0;
        mutable copy = number;
        while (copy % 2 == 0) {
            set nZeroes += 1;
            set copy /= 2;
        }
        return nZeroes;
    }

    /// # Summary
    /// An implementation for `CNOT` that when controlled using a single control uses
    /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
    internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
        body (...) {
            CNOT(a, b);
        }

        adjoint self;

        controlled (ctls, ...) {
            // In this application this operation is used in a way that
            // it is controlled by at most one qubit.
            Fact(Length(ctls) <= 1, "At most one control line allowed");

            if IsEmpty(ctls) {
                CNOT(a, b);
            } else {
                use q = Qubit();
                within {
                    ApplyAnd(Head(ctls), a, q);
                } apply {
                    CNOT(q, b);
                }
            }
        }

        controlled adjoint self;
    }

Exécuter l’estimateur de ressources

L’estimateur de ressources offre six paramètres qubit prédéfinis, dont quatre ont des jeux d’instructions basés sur la porte et deux qui ont un jeu d’instructions Majorana. Il offre également deux codes de correction d’erreur quantique et surface_code floquet_code.

Dans cet exemple, vous exécutez l’estimateur de ressources à l’aide du paramètre qubit qubit_gate_us_e3 et du code de correction d’erreur quantique surface_code.

1. Sélectionnez Affichage -> Palette de commandes et tapez « ressource » qui doit afficher l’option Q# : Calculer les estimations des ressources. Vous pouvez également cliquer sur Estimer dans la liste des commandes affichées juste avant l’opération Main . Sélectionnez cette option pour ouvrir la fenêtre Estimateur de ressource.

   

2. Vous pouvez sélectionner un ou plusieurs types de paramètre Qubit + Code de correction d’erreur pour lesquels estimer les ressources. Pour cet exemple, sélectionnez qubit_gate_us_e3, puis cliquez sur OK.

   

3. Spécifiez le budget d’erreur ou acceptez la valeur par défaut : 0,001. Pour cet exemple, laissez la valeur par défaut et appuyez sur Entrée.

4. Appuyez sur Entrée pour accepter le nom de résultat par défaut en fonction du nom de fichier, dans ce cas, ShorRE.

Afficher les résultats

L’estimateur de ressources fournit plusieurs estimations pour le même algorithme, chacune affichant des compromis entre le nombre de qubits et le runtime. Comprendre le compromis entre l’exécution et la mise à l’échelle du système est l’un des aspects les plus importants de l’estimation des ressources.

Le résultat de l’estimation des ressources s’affiche dans la fenêtre Estimation Q#.

1. L’onglet Résultats affiche un résumé de l’estimation des ressources. Cliquez sur l’icône en regard de la première ligne pour sélectionner les colonnes à afficher. Vous pouvez sélectionner parmi le nom d’exécution, le type d’estimation, le type qubit, le schéma qec, le budget d’erreur, les qubits logiques, la profondeur logique, la distance du code, les états T, les fabriques T, la fraction de fabrique T, le runtime, rQOPS et les qubits physiques.

   

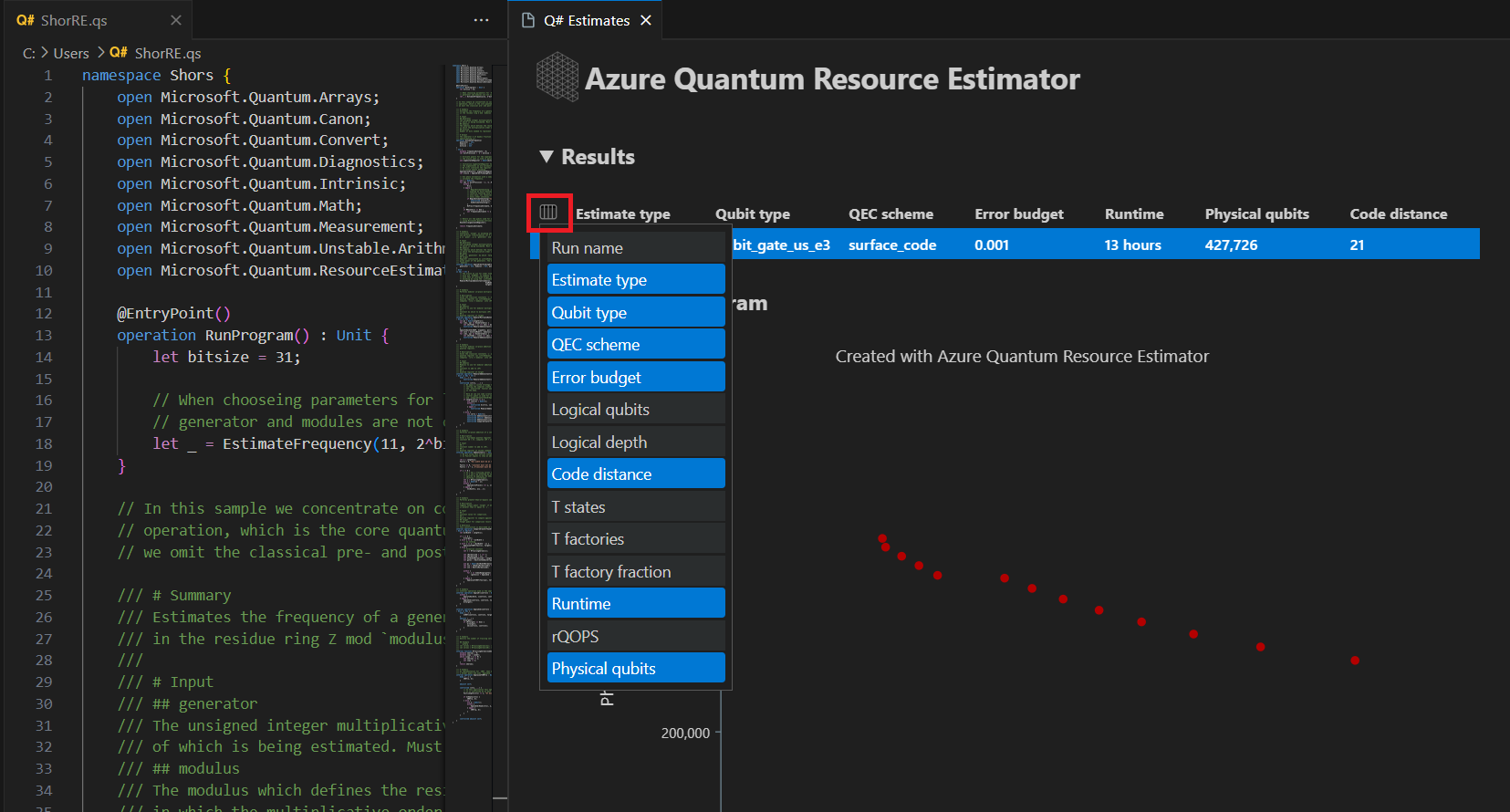
   Dans la colonne Estimer le type de la table de résultats, vous pouvez voir le nombre de combinaisons optimales de {nombre de qubits, runtime} pour votre algorithme. Ces combinaisons sont visibles dans le diagramme d’espace-temps.

2. Le diagramme espace-temps montre les compromis entre le nombre de qubits physiques et le runtime de l’algorithme. Dans ce cas, l’estimateur de ressources trouve 13 combinaisons optimales différentes sur plusieurs milliers possibles. Vous pouvez pointer sur chaque {nombre de qubits, runtime} point pour afficher les détails de l’estimation des ressources à ce stade.

   

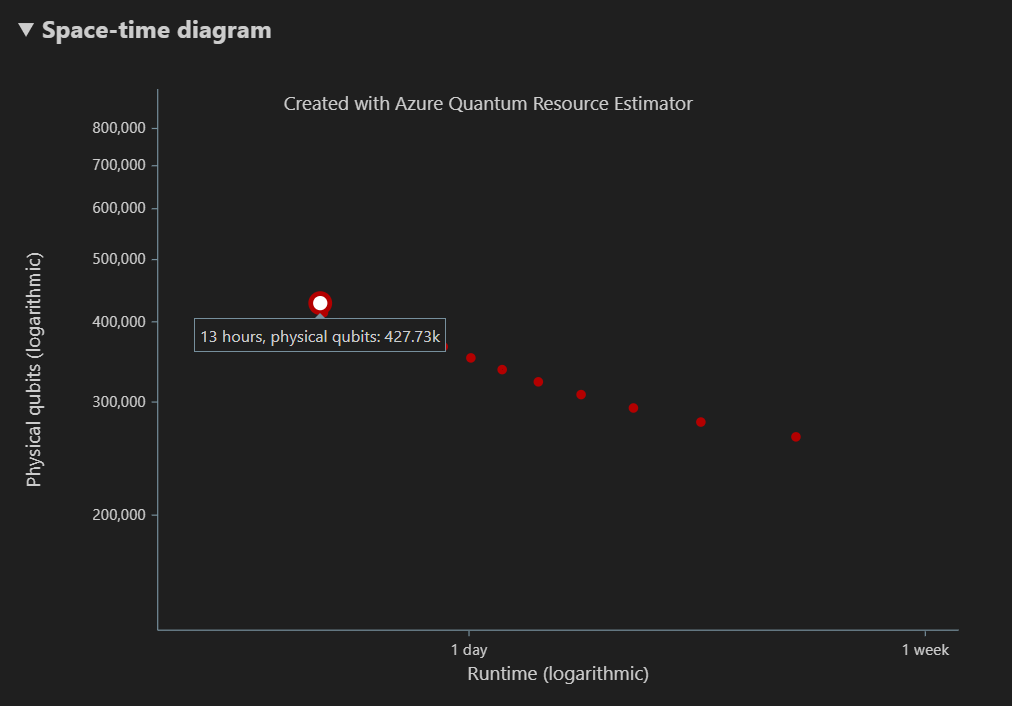
   Pour plus d’informations, consultez le diagramme espace-temps.

   Remarque

   Vous devez cliquer sur un point du diagramme espace-temps, qui est un {nombre de qubits, paire runtime}, pour afficher le diagramme d’espace et les détails de l’estimation de ressource correspondant à ce point.

3. Le diagramme d’espace montre la distribution des qubits physiques utilisés pour l’algorithme et les fabriques T, correspondant à un {nombre de qubits, paire runtime}. Par exemple, si vous sélectionnez le point le plus à gauche dans le diagramme espace-temps, le nombre de qubits physiques nécessaires à l’exécution de l’algorithme est 427726, 196686 dont les qubits d’algorithme et 231040 sont des qubits de fabrique T.

   

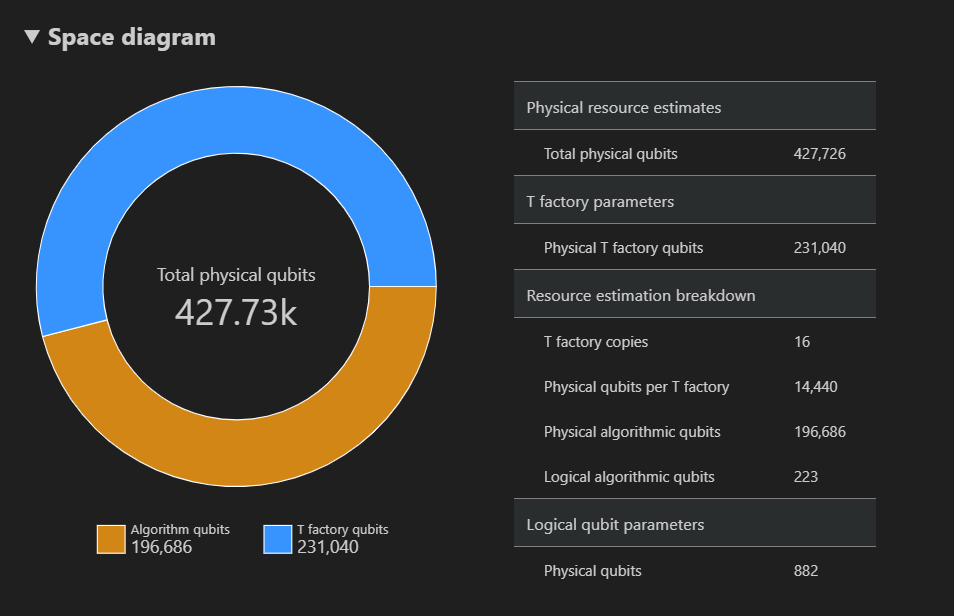
4. Enfin, l’onglet Estimations des ressources affiche la liste complète des données de sortie pour l’estimateur de ressources correspondant à un {nombre de qubits, paire runtime} . Vous pouvez examiner les détails des coûts en réduisant les groupes, qui ont plus d’informations. Par exemple, sélectionnez le point le plus à gauche dans le diagramme d’espace-temps et réduisez le groupe de paramètres qubit logique.

   Paramètre des qubits logiques	Valeur
   Schéma QEC	surface_code
   Distance du code	21
   Qubits physiques	882
   Durée de cycle logique	13 millisecs
   Taux d’erreur des qubits logiques	3,00E-13
   Préfacteur de croisement	0,03
   Seuil de correction d’erreurs	0,01
   Formule de durée de cycle logique	(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance
   Formule des qubits physiques	2 * codeDistance * codeDistance

   Conseil

   Cliquez sur Afficher les lignes détaillées pour afficher la description de chaque sortie des données du rapport.

   Pour plus d’informations, consultez les données de rapport complètes de l’estimateur de ressources.

Modifier les target paramètres

Vous pouvez estimer le coût du même programme Q# à l’aide d’un autre type qubit, d’un code de correction d’erreur et d’un budget d’erreur. Ouvrez la fenêtre Estimateur de ressources en sélectionnant Affichage -> Palette de commandes, puis tapez Q#: Calculate Resource Estimates.

Sélectionnez une autre configuration, par exemple le paramètre qubit basé sur Majorana. qubit_maj_ns_e6 Acceptez la valeur de budget d’erreur par défaut ou entrez-en une nouvelle, puis appuyez sur Entrée. L’estimateur de ressources réexécute l’estimation avec les nouveaux target paramètres.

Pour plus d’informations, consultez Target les paramètres de l’estimateur de ressource.

Exécuter plusieurs configurations de paramètres

L’estimateur de ressources Azure Quantum peut exécuter plusieurs configurations de target paramètres et comparer les résultats d’estimation des ressources.

1. Sélectionnez Affichage -> Palette de commandes, ou appuyez sur Ctrl+Maj+P, puis tapez Q#: Calculate Resource Estimates.

2. Sélectionnez qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code, puis qubit_maj_ns_e6 + floquet_code, puis cliquez sur OK.

3. Acceptez la valeur budgétaire d’erreur par défaut 0.001, puis appuyez sur Entrée.

4. Appuyez sur Entrée pour accepter le fichier d’entrée, dans ce cas, ShorRE.qs.

5. Dans le cas de plusieurs configurations de paramètres, les résultats sont affichés dans différentes lignes de l’onglet Résultats .

6. Le diagramme espace-temps affiche les résultats de toutes les configurations de paramètres. La première colonne de la table de résultats affiche la légende pour chaque configuration de paramètres. Vous pouvez pointer sur chaque point pour afficher les détails de l’estimation des ressources à ce stade.

   

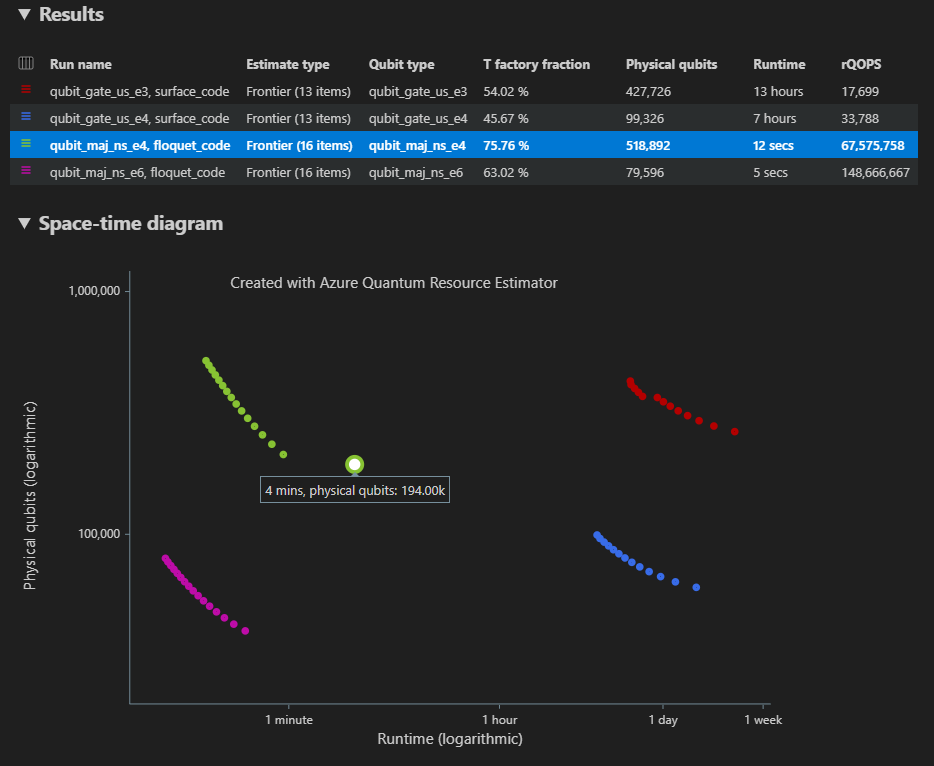
7. Cliquez sur un {nombre de qubits, runtime} point du diagramme espace-temps pour afficher le diagramme d’espace et les données de rapport correspondantes.

Conditions préalables pour Jupyter Notebook dans VS Code

• Un environnement Python avec Python et Pip installés.

• La dernière version de Visual Studio Code ou ouvrir VS Code sur le web.

• VS Code avec les extensions Azure Quantum Development Kit, Python et Jupyter installées.

• Les derniers packages et qsharp-widgets Azure Quantumqsharp.

  python -m pip install --upgrade qsharp qsharp-widgets 
  

Conseil

Vous n’avez pas besoin d’avoir un compte Azure pour exécuter l’estimateur de ressource local.

Créer l’algorithme quantique

1. Dans VS Code, sélectionnez Affichage > Palette de commandes, puis sélectionnez Créer : Notebook Jupyter.

2. En haut à droite, VS Code détecte et affiche la version de Python et l’environnement Python virtuel sélectionné pour le notebook. Si vous avez plusieurs environnements Python, vous devrez peut-être sélectionner un noyau à l’aide du sélecteur de noyau en haut à droite. Si aucun environnement n’a été détecté, consultez Jupyter Notebooks dans VS Code pour obtenir des informations de configuration.

3. Dans la première cellule du notebook, importez le package qsharp.

   import qsharp
   

4. Ajoutez une nouvelle cellule, puis copiez le code suivant.

   %%qsharp
   import Std.Arrays.*;
   import Std.Canon.*;
   import Std.Convert.*;
   import Std.Diagnostics.*;
   import Std.Math.*;
   import Std.Measurement.*;
   import Microsoft.Quantum.Unstable.Arithmetic.*;
   import Std.ResourceEstimation.*;
   
   operation RunProgram() : Unit {
       let bitsize = 31;
   
       // When choosing parameters for `EstimateFrequency`, make sure that
       // generator and modules are not co-prime
       let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
   }
   
   
   // In this sample we concentrate on costing the `EstimateFrequency`
   // operation, which is the core quantum operation in Shors algorithm, and
   // we omit the classical pre- and post-processing.
   
   /// # Summary
   /// Estimates the frequency of a generator
   /// in the residue ring Z mod `modulus`.
   ///
   /// # Input
   /// ## generator
   /// The unsigned integer multiplicative order (period)
   /// of which is being estimated. Must be co-prime to `modulus`.
   /// ## modulus
   /// The modulus which defines the residue ring Z mod `modulus`
   /// in which the multiplicative order of `generator` is being estimated.
   /// ## bitsize
   /// Number of bits needed to represent the modulus.
   ///
   /// # Output
   /// The numerator k of dyadic fraction k/2^bitsPrecision
   /// approximating s/r.
   operation EstimateFrequency(
       generator : Int,
       modulus : Int,
       bitsize : Int
   )
   : Int {
       mutable frequencyEstimate = 0;
       let bitsPrecision =  2 * bitsize + 1;
   
       // Allocate qubits for the superposition of eigenstates of
       // the oracle that is used in period finding.
       use eigenstateRegister = Qubit[bitsize];
   
       // Initialize eigenstateRegister to 1, which is a superposition of
       // the eigenstates we are estimating the phases of.
       // We first interpret the register as encoding an unsigned integer
       // in little endian encoding.
       ApplyXorInPlace(1, eigenstateRegister);
       let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
   
       // Use phase estimation with a semiclassical Fourier transform to
       // estimate the frequency.
       use c = Qubit();
       for idx in bitsPrecision - 1..-1..0 {
           within {
               H(c);
           } apply {
               // `BeginEstimateCaching` and `EndEstimateCaching` are the operations
               // exposed by Azure Quantum Resource Estimator. These will instruct
               // resource counting such that the if-block will be executed
               // only once, its resources will be cached, and appended in
               // every other iteration.
               if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
                   Controlled oracle([c], (1 <<< idx, eigenstateRegister));
                   EndEstimateCaching();
               }
               R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
           }
           if MResetZ(c) == One {
               set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
           }
       }
   
       // Return all the qubits used for oracle eigenstate back to 0 state
       // using Microsoft.Quantum.Intrinsic.ResetAll.
       ResetAll(eigenstateRegister);
   
       return frequencyEstimate;
   }
   
   /// # Summary
   /// Interprets `target` as encoding unsigned little-endian integer k
   /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
   /// p is `power`, g is `generator` and N is `modulus`.
   ///
   /// # Input
   /// ## generator
   /// The unsigned integer multiplicative order ( period )
   /// of which is being estimated. Must be co-prime to `modulus`.
   /// ## modulus
   /// The modulus which defines the residue ring Z mod `modulus`
   /// in which the multiplicative order of `generator` is being estimated.
   /// ## power
   /// Power of `generator` by which `target` is multiplied.
   /// ## target
   /// Register interpreted as little endian encoded which is multiplied by
   /// given power of the generator. The multiplication is performed modulo
   /// `modulus`.
   internal operation ApplyOrderFindingOracle(
       generator : Int, modulus : Int, power : Int, target : Qubit[]
   )
   : Unit
   is Adj + Ctl {
       // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
       // also use `ExpModI` to compute a by which x must be multiplied. Also
       // note that we interpret target as unsigned integer in little-endian
       // encoding.
       ModularMultiplyByConstant(modulus,
                                   ExpModI(generator, power, modulus),
                                   target);
   }
   
   /// # Summary
   /// Performs modular in-place multiplication by a classical constant.
   ///
   /// # Description
   /// Given the classical constants `c` and `modulus`, and an input
   /// quantum register |𝑦⟩, this operation
   /// computes `(c*x) % modulus` into |𝑦⟩.
   ///
   /// # Input
   /// ## modulus
   /// Modulus to use for modular multiplication
   /// ## c
   /// Constant by which to multiply |𝑦⟩
   /// ## y
   /// Quantum register of target
   internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
   : Unit is Adj + Ctl {
       use qs = Qubit[Length(y)];
       for (idx, yq) in Enumerated(y) {
           let shiftedC = (c <<< idx) % modulus;
           Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
       }
       ApplyToEachCA(SWAP, Zipped(y, qs));
       let invC = InverseModI(c, modulus);
       for (idx, yq) in Enumerated(y) {
           let shiftedC = (invC <<< idx) % modulus;
           Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
       }
   }
   
   /// # Summary
   /// Performs modular in-place addition of a classical constant into a
   /// quantum register.
   ///
   /// # Description
   /// Given the classical constants `c` and `modulus`, and an input
   /// quantum register  |𝑦⟩, this operation
   /// computes `(x+c) % modulus` into |𝑦⟩.
   ///
   /// # Input
   /// ## modulus
   /// Modulus to use for modular addition
   /// ## c
   /// Constant to add to |𝑦⟩
   /// ## y
   /// Quantum register of target
   internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
   : Unit is Adj + Ctl {
       body (...) {
           Controlled ModularAddConstant([], (modulus, c, y));
       }
       controlled (ctrls, ...) {
           // We apply a custom strategy to control this operation instead of
           // letting the compiler create the controlled variant for us in which
           // the `Controlled` functor would be distributed over each operation
           // in the body.
           //
           // Here we can use some scratch memory to save ensure that at most one
           // control qubit is used for costly operations such as `AddConstant`
           // and `CompareGreaterThenOrEqualConstant`.
           if Length(ctrls) >= 2 {
               use control = Qubit();
               within {
                   Controlled X(ctrls, control);
               } apply {
                   Controlled ModularAddConstant([control], (modulus, c, y));
               }
           } else {
               use carry = Qubit();
               Controlled AddConstant(ctrls, (c, y + [carry]));
               Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
               Controlled AddConstant([carry], (modulus, y));
               Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
           }
       }
   }
   
   /// # Summary
   /// Performs in-place addition of a constant into a quantum register.
   ///
   /// # Description
   /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
   /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
   ///
   /// # Input
   /// ## c
   /// Constant number to add to |𝑦⟩.
   /// ## y
   /// Quantum register of second summand and target; must not be empty.
   internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
       // We are using this version instead of the library version that is based
       // on Fourier angles to show an advantage of sparse simulation in this sample.
   
       let n = Length(y);
       Fact(n > 0, "Bit width must be at least 1");
   
       Fact(c >= 0, "constant must not be negative");
       Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
   
       if c != 0 {
           // If c has j trailing zeroes than the j least significant bits
           // of y will not be affected by the addition and can therefore be
           // ignored by applying the addition only to the other qubits and
           // shifting c accordingly.
           let j = NTrailingZeroes(c);
           use x = Qubit[n - j];
           within {
               ApplyXorInPlace(c >>> j, x);
           } apply {
               IncByLE(x, y[j...]);
           }
       }
   }
   
   /// # Summary
   /// Performs greater-than-or-equals comparison to a constant.
   ///
   /// # Description
   /// Toggles output qubit `target` if and only if input register `x`
   /// is greater than or equal to `c`.
   ///
   /// # Input
   /// ## c
   /// Constant value for comparison.
   /// ## x
   /// Quantum register to compare against.
   /// ## target
   /// Target qubit for comparison result.
   ///
   /// # Reference
   /// This construction is described in [Lemma 3, arXiv:2201.10200]
   internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
   : Unit is Adj+Ctl {
       let bitWidth = Length(x);
   
       if c == 0 {
           X(target);
       } elif c >= 2 ^ bitWidth {
           // do nothing
       } elif c == 2 ^ (bitWidth - 1) {
           ApplyLowTCNOT(Tail(x), target);
       } else {
           // normalize constant
           let l = NTrailingZeroes(c);
   
           let cNormalized = c >>> l;
           let xNormalized = x[l...];
           let bitWidthNormalized = Length(xNormalized);
           let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
   
           use qs = Qubit[bitWidthNormalized - 1];
           let cs1 = [Head(xNormalized)] + Most(qs);
           let cs2 = Rest(xNormalized);
   
           within {
               for i in IndexRange(gates) {
                   (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
               }
           } apply {
               ApplyLowTCNOT(Tail(qs), target);
           }
       }
   }
   
   /// # Summary
   /// Internal operation used in the implementation of GreaterThanOrEqualConstant.
   internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
       within {
           ApplyToEachA(X, [control1, control2]);
       } apply {
           ApplyAnd(control1, control2, target);
           X(target);
       }
   }
   
   internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
   : Unit is Adj {
       body (...) {
           CCNOT(control1, control2, target);
       }
       adjoint (...) {
           H(target);
           if (M(target) == One) {
               X(target);
               CZ(control1, control2);
           }
       }
   }
   
   
   /// # Summary
   /// Returns the number of trailing zeroes of a number
   ///
   /// ## Example
   /// ```qsharp
   /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
   /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
   /// ```
   internal function NTrailingZeroes(number : Int) : Int {
       mutable nZeroes = 0;
       mutable copy = number;
       while (copy % 2 == 0) {
           set nZeroes += 1;
           set copy /= 2;
       }
       return nZeroes;
   }
   
   /// # Summary
   /// An implementation for `CNOT` that when controlled using a single control uses
   /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
   internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
       body (...) {
           CNOT(a, b);
       }
   
       adjoint self;
   
       controlled (ctls, ...) {
           // In this application this operation is used in a way that
           // it is controlled by at most one qubit.
           Fact(Length(ctls) <= 1, "At most one control line allowed");
   
           if IsEmpty(ctls) {
               CNOT(a, b);
           } else {
               use q = Qubit();
               within {
                   ApplyAnd(Head(ctls), a, q);
               } apply {
                   CNOT(q, b);
               }
           }
       }
   
       controlled adjoint self;
   }
   

Estimer l’algorithme quantique

À présent, vous allez estimer les ressources physiques de l’opération RunProgram à l’aide des hypothèses par défaut. Ajoutez une nouvelle cellule, puis copiez le code suivant.

result = qsharp.estimate("RunProgram()")
result

La fonction qsharp.estimate crée un objet de résultat, qui permet d’afficher un tableau avec le nombre global de ressources physiques. Vous pouvez examiner les détails des coûts en réduisant les groupes, qui ont plus d’informations. Pour plus d’informations, consultez les données de rapport complètes de l’estimateur de ressources.

Par exemple, réduisez le groupe Paramètres des qubits logiques pour voir que la distance de code est de 21, et que le nombre de qubits physiques est de 882.

Paramètre des qubits logiques	Valeur
Schéma QEC	surface_code
Distance du code	21
Qubits physiques	882
Durée de cycle logique	8 millisecs
Taux d’erreur des qubits logiques	3,00E-13
Préfacteur de croisement	0,03
Seuil de correction d’erreurs	0,01
Formule de durée de cycle logique	(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance
Formule des qubits physiques	2 * codeDistance * codeDistance

Conseil

Pour une version plus compacte de la table de sortie, vous pouvez utiliser result.summary.

Diagramme d’espace

La distribution des qubits physiques utilisés pour l’algorithme et les fabriques T est un facteur qui peut impacter la conception de votre algorithme. Vous pouvez utiliser le package qsharp-widgets pour visualiser cette distribution afin de mieux comprendre l’estimation de l’espace nécessaire à l’algorithme.

from qsharp-widgets import SpaceChart, EstimateDetails
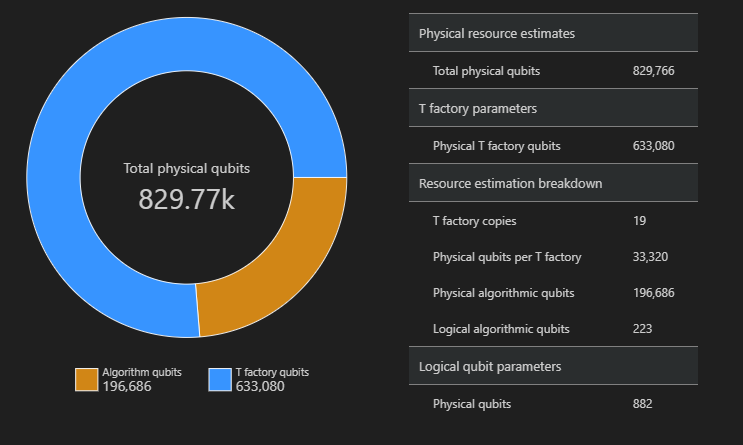
SpaceChart(result)

Dans cet exemple, le nombre de qubits physiques nécessaires à l’exécution de l’algorithme est de 829 766, dont 196 686 sont des qubits d’algorithme et 633 080 sont des qubits de fabrique T.

Modifier les valeurs par défaut et estimer l’algorithme

Lorsque vous soumettez une requête d'estimation des ressources pour votre programme, vous pouvez spécifier certains paramètres facultatifs. Utilisez le jobParams champ pour accéder à tous les target paramètres qui peuvent être passés à l’exécution du travail et voir quelles valeurs par défaut ont été supposées :

result['jobParams']

{'errorBudget': 0.001,
 'qecScheme': {'crossingPrefactor': 0.03,
  'errorCorrectionThreshold': 0.01,
  'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
  'name': 'surface_code',
  'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
 'qubitParams': {'instructionSet': 'GateBased',
  'name': 'qubit_gate_ns_e3',
  'oneQubitGateErrorRate': 0.001,
  'oneQubitGateTime': '50 ns',
  'oneQubitMeasurementErrorRate': 0.001,
  'oneQubitMeasurementTime': '100 ns',
  'tGateErrorRate': 0.001,
  'tGateTime': '50 ns',
  'twoQubitGateErrorRate': 0.001,
  'twoQubitGateTime': '50 ns'}}

Vous pouvez voir que l’estimateur de ressources prend le modèle qubit qubit_gate_ns_e3, le code de correction d’erreur surface_code et le budget d’erreur 0,001 comme valeurs par défaut pour l’estimation.

Voici les target paramètres qui peuvent être personnalisés :

• errorBudget : l’erreur globale de budget autorisée pour l’algorithme
• qecScheme : le schéma de correction des erreurs quantiques (QEC)
• qubitParams : les paramètres qubit physiques
• constraints : contraintes au niveau du composant
• distillationUnitSpecifications : les spécifications des algorithmes de distillation pour les fabriques T
• estimateType : unique ou frontière

Pour plus d’informations, consultez Target les paramètres de l’estimateur de ressource.

Modifier le modèle de qubit

Vous pouvez estimer le coût pour le même algorithme à l’aide du paramètre qubit basé sur Majorana, qubitParams, « qubit_maj_ns_e6 ».

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                }})
EstimateDetails(result_maj)

Modifier le schéma de correction des erreurs quantiques

Vous pouvez réexécuter le travail d’estimation des ressources pour le même exemple sur les paramètres qubit basés sur Majorana avec un schéma QEC floqué, qecScheme.

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                },
                "qecScheme": {
                    "name": "floquet_code"
                }})
EstimateDetails(result_maj)

Modifier le budget d’erreur

Ensuite, réexécutez le même circuit quantique avec une errorBudget de 10 %.

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                },
                "qecScheme": {
                    "name": "floquet_code"
                },
                "errorBudget": 0.1})
EstimateDetails(result_maj)

Traitement par lots avec l’estimateur de ressources

L’estimateur de target ressources Azure Quantum vous permet d’exécuter plusieurs paramètres et de comparer les résultats. Cela est utile quand vous souhaitez comparer le coût de différents modèles de qubits, schémas QEC ou budgets d’erreur.

1. Vous pouvez effectuer une estimation par lot en passant une liste de target paramètres au params paramètre de la qsharp.estimate fonction. Par exemple, exécutez le même algorithme avec les paramètres par défaut et les paramètres qubit basés sur Majorana avec un schéma QEC floquet.

   result_batch = qsharp.estimate("RunProgram()", params=
                   [{}, # Default parameters
                   {
                       "qubitParams": {
                           "name": "qubit_maj_ns_e6"
                       },
                       "qecScheme": {
                           "name": "floquet_code"
                       }
                   }])
   result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])
   

   Modèle	Qubits logiques	Profondeur logique	États T	Distance du code	Fabriques T	Fraction de fabrique T	Qubits physiques	rQOPS	Temps d’exécution physique
   Basé sur une porte, ns, 10⁻³	223	3,64 M	4,70 M	21	19	76.30 %	829,77k	26,55 M	31 secondes
   Majorana ns, 10⁻⁶	223	3,64 M	4,70 M	5	19	63.02 %	79,60k	148,67 M	5 secondes

2. Vous pouvez également construire une liste de paramètres d’estimation à l’aide de la EstimatorParams classe.

   from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts
   
   labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"]
   
   params = EstimatorParams(num_items=6)
   params.error_budget = 0.333
   params.items[0].qubit_params.name = QubitParams.GATE_US_E3
   params.items[1].qubit_params.name = QubitParams.GATE_US_E4
   params.items[2].qubit_params.name = QubitParams.GATE_NS_E3
   params.items[3].qubit_params.name = QubitParams.GATE_NS_E4
   params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4
   params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE
   params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6
   params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODE
   

   qsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)
   

   Modèle	Qubits logiques	Profondeur logique	États T	Distance du code	Fabriques T	Fraction de fabrique T	Qubits physiques	rQOPS	Temps d’exécution physique
   Basé sur une porte, µs, 10⁻³	223 3,64 M	4,70 M	17	13	40,54 %	216,77 k	21,86 k	10 heures
   Basé sur une porte, µs, 10⁻⁴	223	3,64 M	4,70 M	9	14	43,17 %	63,57 k	41,30 k	5 heures
   Basé sur une porte, ns, 10⁻³	223 3,64 M	4,70 M	17	16	69,08 %	416,89 k	32,79 M	25 s
   Basé sur une porte, ns, 10⁻⁴	223 3,64 M	4,70 M	9	14	43,17 %	63,57 k	61,94 M	13 s
   Majorana ns, 10⁻⁴	223 3,64 M	4,70 M	9	19	82,75 %	501,48 k	82,59 M	10 s
   Majorana ns, 10⁻⁶	223 3,64 M	4,70 M	5	13	31,47 %	42,96 k	148,67 M	5 secondes

Exécution de l’estimation de la frontière pareto

Lors de l’estimation des ressources d’un algorithme, il est important de prendre en compte le compromis entre le nombre de qubits physiques et le runtime de l’algorithme. Vous pouvez envisager d’allouer autant de qubits physiques que possible pour réduire le runtime de l’algorithme. Toutefois, le nombre de qubits physiques est limité par le nombre de qubits physiques disponibles dans le matériel quantique.

L’estimation de la frontière Pareto fournit plusieurs estimations pour le même algorithme, chacune avec un compromis entre le nombre de qubits et le runtime.

1. Pour exécuter l’estimateur de ressources à l’aide de l’estimation de la frontière Pareto, vous devez spécifier le "estimateType"target paramètre en tant que "frontier". Par exemple, exécutez le même algorithme avec les paramètres qubit basés sur Majorana avec un code surface à l’aide de l’estimation de la frontière Pareto.

   result = qsharp.estimate("RunProgram()", params=
                               {"qubitParams": { "name": "qubit_maj_ns_e4" },
                               "qecScheme": { "name": "surface_code" },
                               "estimateType": "frontier", # frontier estimation
                               }
                           )
   

2. Vous pouvez utiliser la EstimatesOverview fonction pour afficher une table avec le nombre global de ressources physiques. Cliquez sur l’icône en regard de la première ligne pour sélectionner les colonnes à afficher. Vous pouvez sélectionner parmi le nom d’exécution, le type d’estimation, le type qubit, le schéma qec, le budget d’erreur, les qubits logiques, la profondeur logique, la distance du code, les états T, les fabriques T, la fraction de fabrique T, le runtime, rQOPS et les qubits physiques.

   from qsharp_widgets import EstimatesOverview
   EstimatesOverview(result)
   

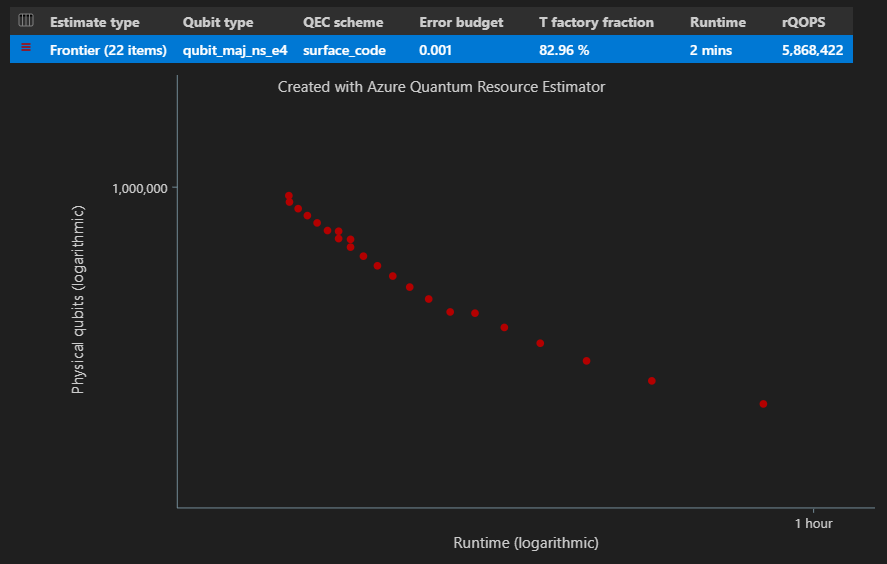
Dans la colonne Estimer le type de la table de résultats, vous pouvez voir le nombre de combinaisons différentes de {nombre de qubits, runtime} pour votre algorithme. Dans ce cas, l’estimateur de ressources trouve 22 combinaisons optimales différentes sur plusieurs milliers possibles.

Diagramme d’espace-temps

La EstimatesOverview fonction affiche également le diagramme d’espace-temps de l’estimateur de ressources.

Le diagramme espace-temps montre le nombre de qubits physiques et le runtime de l’algorithme pour chaque {nombre de qubits, paire runtime}. Vous pouvez pointer sur chaque point pour afficher les détails de l’estimation des ressources à ce stade.

Traitement par lots avec estimation de la frontière Pareto

1. Pour estimer et comparer plusieurs configurations de target paramètres avec estimation de frontière, ajoutez-y "estimateType": "frontier", .

   result = qsharp.estimate(
       "RunProgram()",
       [
           {
           "qubitParams": { "name": "qubit_maj_ns_e4" },
           "qecScheme": { "name": "surface_code" },
           "estimateType": "frontier", # Pareto frontier estimation
           },
           {
           "qubitParams": { "name": "qubit_maj_ns_e6" },
           "qecScheme": { "name": "floquet_code" },
           "estimateType": "frontier", # Pareto frontier estimation
           },
       ]
   )
   
   EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])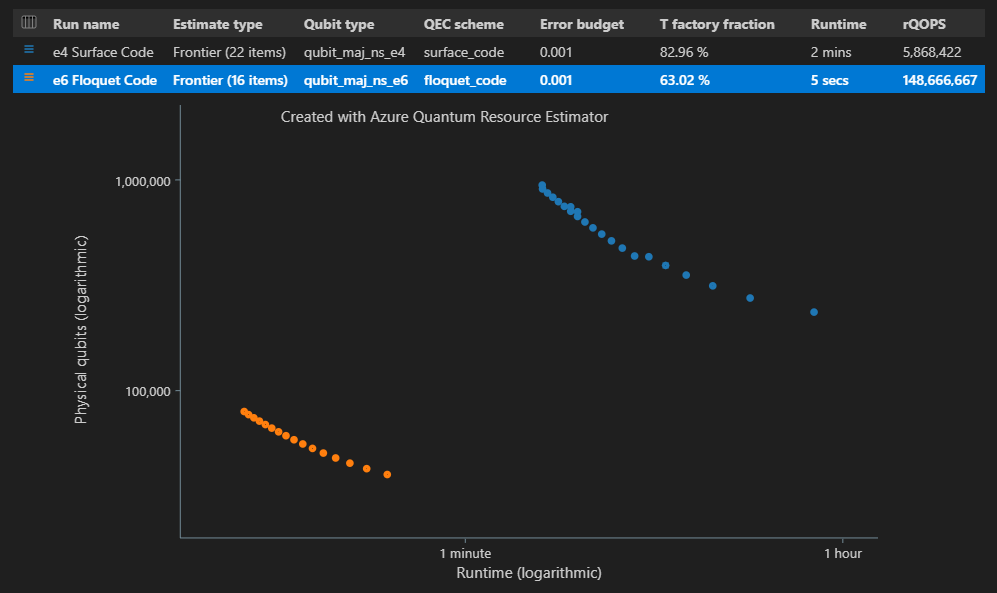
   

   

   Remarque

   Vous pouvez définir des couleurs et exécuter des noms pour le diagramme qubit-time à l’aide de la EstimatesOverview fonction.

2. Lors de l’exécution de plusieurs configurations de paramètres à l’aide de target l’estimation de frontière Pareto, vous pouvez voir les estimations de ressources pour un point spécifique du diagramme espace-temps, c’est-à-dire pour chaque {nombre de qubits, paire runtime}. Par exemple, le code suivant montre l’utilisation des détails d’estimation pour la deuxième exécution (estimation index=0) et le quatrième (index de point=3) runtime le plus court.

   EstimateDetails(result[1], 4)
   

3. Vous pouvez également voir le diagramme d’espace pour un point spécifique du diagramme d’espace-temps. Par exemple, le code suivant montre le diagramme d’espace pour la première série de combinaisons (estimate index=0) et le troisième runtime le plus court (point index=2).

   SpaceChart(result[0], 2)
   

Conditions préalables pour Qiskit

• Un compte Azure avec un abonnement actif. Si vous n’avez pas de compte Azure, inscrivez-vous gratuitement et inscrivez-vous à un abonnement de paiement à l’utilisation.
• Un espace de travail Azure Quantum. Pour plus d’informations, consultez Créer un espace de travail Azure Quantum.

Activer l’estimateur target de ressources Azure Quantum dans votre espace de travail

L’estimateur de ressources est un target fournisseur Microsoft Quantum Computing. Si vous avez créé un espace de travail depuis la publication de l’estimateur de ressources, le fournisseur Microsoft Quantum Computing a été ajouté automatiquement à votre espace de travail.

Si vous utilisez un espace de travail Azure Quantum existant :

1. Ouvrez votre espace de travail dans le portail Azure.
2. Dans le panneau de gauche, sous Opérations, sélectionnez Fournisseurs.
3. Sélectionnez + Ajouter un fournisseur.
4. Sélectionnez + Ajouter pour Microsoft Quantum Computing.
5. Sélectionnez Learn &Développer et sélectionnez Ajouter.

Créer un notebook dans votre espace de travail

1. Connectez-vous au Portail Azure et sélectionnez votre espace de travail Quantum Azure.
2. Sous Opérations, sélectionnez Notebooks
3. Cliquez sur Mes blocs-notes , puis cliquez sur Ajouter un nouveau
4. Dans Type de noyau, sélectionnez IPython.
5. Tapez un nom pour le fichier, puis cliquez sur Créer un fichier.

Quand votre nouveau notebook s’ouvre, il crée automatiquement le code de la première cellule, en fonction de vos informations d’abonnement et d’espace de travail.

from azure.quantum import Workspace
workspace = Workspace ( 
    resource_id = "", # Your resource_id 
    location = ""  # Your workspace location (for example, "westus") 
)

Remarque

Sauf indication contraire, vous devez exécuter chaque cellule dans l’ordre de création pour éviter les problèmes de compilation.

Cliquez sur l’icône triangulaire « lecture » à gauche de la cellule pour exécuter le code.

Charger les importations requises

Tout d’abord, vous devez importer des modules supplémentaires à partir d’azure-quantum et qiskit.

Cliquez sur + Code pour ajouter une nouvelle cellule, puis ajoutez et exécutez le code suivant :

from azure.quantum.qiskit import AzureQuantumProvider
from qiskit import QuantumCircuit, transpile
from qiskit.circuit.library import RGQFTMultiplier

Se connecter au service Azure Quantum

Ensuite, créez un objet AzureQuantumProvider à l’aide de l’objet workspace de la cellule précédente pour vous connecter à votre espace de travail Azure Quantum. Vous créez une instance back-end et définissez l’estimateur de ressource comme votre target.

provider = AzureQuantumProvider(workspace)
backend = provider.get_backend('microsoft.estimator')

Créer l’algorithme quantique

Dans cet exemple, vous créez un circuit quantique pour un multiplicateur basé sur la construction présentée dans Ruiz-Perez et Garcia-Escartin (arXiv :1411.5949) qui utilise la transformation de Fourier quantique pour implémenter l’arithmétique.

Vous pouvez ajuster la taille du multiplicateur en modifiant la bitwidth variable. La génération de circuit est encapsulée dans une fonction qui peut être appelée avec la bitwidth valeur du multiplicateur. L’opération aura deux registres d’entrée, chacune la taille du registre spécifié bitwidthet un registre de sortie qui est deux fois la taille de l’objet spécifié bitwidth. La fonction imprime également certains nombres de ressources logiques pour le multiplicateur extrait directement du circuit quantique.

def create_algorithm(bitwidth):
    print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
    
    # Print a warning for large bitwidths that will require some time to generate and
    # transpile the circuit.
    if bitwidth > 18:
        print(f"[WARN] It will take more than one minute generate a quantum circuit with a bitwidth larger than 18")

    circ = RGQFTMultiplier(num_state_qubits=bitwidth, num_result_qubits=2 * bitwidth)

    # One could further reduce the resource estimates by increasing the optimization_level,
    # however, this will also increase the runtime to construct the algorithm.  Note, that
    # it does not affect the runtime for resource estimation.
    print(f"[INFO] Decompose circuit into intrinsic quantum operations")

    circ = transpile(circ, basis_gates=SUPPORTED_INSTRUCTIONS, optimization_level=0)

    # print some statistics
    print(f"[INFO]   qubit count: {circ.num_qubits}")
    print("[INFO]   gate counts")
    for gate, count in circ.count_ops().items():
        print(f"[INFO]   - {gate}: {count}")

    return circ

Remarque

Vous pouvez envoyer des travaux d’estimation de ressources physiques pour les algorithmes qui n’ont aucun état T, mais qui ont au moins une mesure.

Estimer l’algorithme quantique

Créez une instance de votre algorithme à l’aide de la create_algorithm fonction. Vous pouvez ajuster la taille du multiplicateur en modifiant la bitwidth variable.

bitwidth = 4

circ = create_algorithm(bitwidth)

Estimer les ressources physiques de cette opération à l’aide des hypothèses par défaut. Vous pouvez envoyer le circuit au serveur principal de l’estimateur de ressources à l’aide de la run méthode, puis exécuter job.result() pour attendre que le travail se termine et retourne les résultats.

job = backend.run(circ)
result = job.result()
result

Cela crée une table qui affiche le nombre global de ressources physiques. Vous pouvez examiner les détails des coûts en réduisant les groupes, qui ont plus d’informations.

Conseil

Pour une version plus compacte de la table de sortie, vous pouvez utiliser result.summary.

Par exemple, si vous réduisez le groupe de paramètres qubit logique, vous pouvez voir plus facilement que la distance du code de correction d’erreur est 15.

Paramètre des qubits logiques	Valeur
Schéma QEC	surface_code
Distance du code	15
Qubits physiques	450
Durée de cycle logique	6us
Taux d’erreur des qubits logiques	3.00E-10
Préfacteur de croisement	0,03
Seuil de correction d’erreurs	0,01
Formule de durée de cycle logique	(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance
Formule des qubits physiques	2 * codeDistance * codeDistance

Dans le groupe de paramètres qubits physiques, vous pouvez voir les propriétés qubit physiques qui ont été supposées pour cette estimation. Par exemple, le temps nécessaire pour effectuer une mesure à qubit unique et une porte à qubit unique est supposé être respectivement de 100 ns et de 50 ns.

Conseil

Vous pouvez également accéder à la sortie de l’estimateur de ressource en tant que dictionnaire Python à l’aide de la méthode result.data().

Pour plus d’informations, consultez la liste complète des données de sortie pour l’estimateur de ressources.

Diagrammes d’espace

La distribution des qubits physiques utilisés pour l’algorithme et les fabriques T est un facteur qui peut impacter la conception de votre algorithme. Vous pouvez visualiser cette distribution pour mieux comprendre les besoins en espace estimés pour l’algorithme.

result.diagram.space

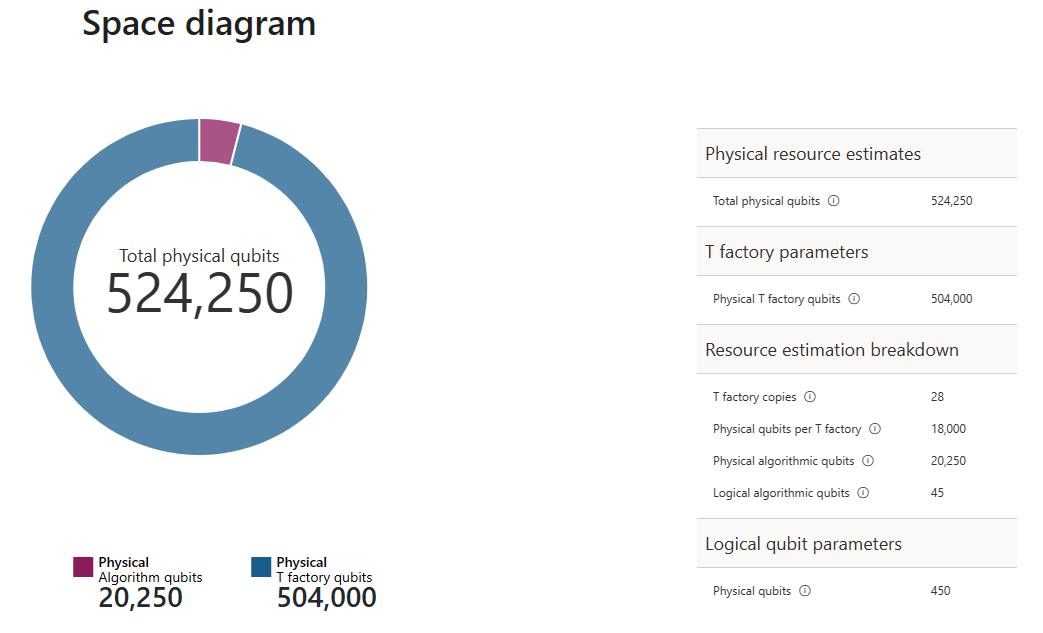
Le diagramme d’espace montre la proportion de qubits d’algorithme et de qubits de fabrique T. Notez que le nombre de copies de fabrique T, 28, contribue au nombre de qubits physiques pour les fabriques T en tant que $\text{T factories} \cdot \text{physical qubit per T factory}= 28 \cdot 18.000 = 504.000$.

Pour plus d’informations, consultez L’estimation physique de la fabrique T.

Modifier les valeurs par défaut et estimer l’algorithme

Lorsque vous soumettez une requête d'estimation des ressources pour votre programme, vous pouvez spécifier certains paramètres facultatifs. Utilisez le jobParams champ pour accéder à toutes les valeurs qui peuvent être passées à l’exécution du travail et voir quelles valeurs par défaut ont été supposées :

result.data()["jobParams"]

{'errorBudget': 0.001,
 'qecScheme': {'crossingPrefactor': 0.03,
  'errorCorrectionThreshold': 0.01,
  'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
  'name': 'surface_code',
  'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
 'qubitParams': {'instructionSet': 'GateBased',
  'name': 'qubit_gate_ns_e3',
  'oneQubitGateErrorRate': 0.001,
  'oneQubitGateTime': '50 ns',
  'oneQubitMeasurementErrorRate': 0.001,
  'oneQubitMeasurementTime': '100 ns',
  'tGateErrorRate': 0.001,
  'tGateTime': '50 ns',
  'twoQubitGateErrorRate': 0.001,
  'twoQubitGateTime': '50 ns'}}

Voici les target paramètres qui peuvent être personnalisés :

• errorBudget - budget d’erreur global autorisé
• qecScheme : le schéma de correction des erreurs quantiques (QEC)
• qubitParams : les paramètres qubit physiques
• constraints : contraintes au niveau du composant
• distillationUnitSpecifications : les spécifications des algorithmes de distillation pour les fabriques T

Pour plus d’informations, consultez Target les paramètres de l’estimateur de ressource.

Modifier le modèle de qubit

Ensuite, estimez le coût pour le même algorithme à l’aide du paramètre qubit basé sur Majorana qubit_maj_ns_e6

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    })
result = job.result()
result

Vous pouvez inspecter les nombres physiques par programme. Par exemple, vous pouvez explorer des détails sur la fabrique T créée pour exécuter l’algorithme.

result.data()["tfactory"]

{'eccDistancePerRound': [1, 1, 5],
 'logicalErrorRate': 1.6833177305222897e-10,
 'moduleNamePerRound': ['15-to-1 space efficient physical',
  '15-to-1 RM prep physical',
  '15-to-1 RM prep logical'],
 'numInputTstates': 20520,
 'numModulesPerRound': [1368, 20, 1],
 'numRounds': 3,
 'numTstates': 1,
 'physicalQubits': 16416,
 'physicalQubitsPerRound': [12, 31, 1550],
 'runtime': 116900.0,
 'runtimePerRound': [4500.0, 2400.0, 110000.0]}

Remarque

Par défaut, le runtime est affiché en nanosecondes.

Vous pouvez utiliser ces données pour produire des explications sur la façon dont les fabriques T produisent les états T requis.

data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]

print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
    print(f"""- {tfactory["numModulesPerRound"][round]} {tfactory["moduleNamePerRound"][round]} unit(s)""")

A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)

Modifier le schéma de correction des erreurs quantiques

À présent, réexécutez le travail d’estimation des ressources pour le même exemple sur les paramètres qubit basés sur Majorana avec un schéma QEC floqued, qecScheme.

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    },
    qecScheme={
        "name": "floquet_code"
    })
result_maj_floquet = job.result()
result_maj_floquet

Modifier le budget d’erreur

Réexécuter le même circuit quantique avec une errorBudget valeur de 10 %.

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    },
    qecScheme={
        "name": "floquet_code"
    },
    errorBudget=0.1)
result_maj_floquet_e1 = job.result()
result_maj_floquet_e1

Remarque

Si vous rencontrez un problème lors de l’utilisation de l’estimateur de ressources, consultez la page Résolution des problèmes ou contactez AzureQuantumInfo@microsoft.com.

Étapes suivantes

• Comprendre les résultats de l’estimateur de ressources
• Personnaliser les estimations de ressources en caractéristiques de l’ordinateur
• Gérer les programmes volumineux avec l’estimateur de ressources
• Tutoriel : Estimer les ressources d’un problème de chimie quantique