Oktatóanyag: Kvantum véletlenszerű számgenerátor implementálása Q#

2025-03-29

Ebben az oktatóanyagban megtanulod egy alapszintű kvantumprogram írását Q#, amely a kvantummechanika természetét felhasználva véletlenszerű számot hoz létre.

Az oktatóanyag során az alábbi lépéseket fogja végrehajtani:

Hozzon létre egy Q# programot.
Tekintse át a program fő összetevőit Q# .
Definiálja a probléma logikáját.
A klasszikus és kvantumműveletek kombinálásával megoldhatja a problémát.
Qubitek és a szuperpozíció használata kvantumos véletlenszám-generátor létrehozásához.

Tipp

Ha fel szeretné gyorsítani a kvantum-számítástechnika folyamatát, tekintse meg az Azure Quantum-webhely egyedi funkcióját, az Azure Quantum-ot. Itt futtathat beépített mintákat vagy saját Q# programokat, új Q# kódot hozhat létre az üzeneteiből, megnyithatja és futtathatja a kódot a WEBES VS Code-ban Q#egy kattintással, és kérdéseket tehet fel a Copilotnak a kvantum-számítástechnikával kapcsolatban.

Előfeltételek

A kódminta futtatása a Copilotban az Azure Quantumban:
- Egy Microsoft (MSA) e-mail-fiók.
A kódminta fejlesztése és futtatása a Visual Studio Code-ban:
- A Visual Studio Code legújabb verziója, vagy nyissa meg a VS Code-ot a weben.
- Az Azure-bővítmény Quantum Development Kitlegújabb verziója. A telepítés részleteiért lásd: QDK-bővítmény beállítása.
- Ha Jupyter Notebookokat szeretne használni, telepítenie kell a Python- és Jupyter-bővítményeket , valamint a legújabb qsharp Python-csomagot is. Ehhez nyisson meg egy terminált, és futtassa a következő parancsot:
```
$ pip install --upgrade  qsharp
```

A probléma meghatározása

A klasszikus számítógépek nem véletlenszerű számokat, hanem pszeudo-számokat hoznak létre. A pszeudorandom számgenerátor egy determinisztikus számsorozatot hoz létre valamilyen kezdeti érték, úgynevezett mag alapján. Hogy minél jobban megközelítsük a véletlenszerű értékeket, a kiinduló érték a leggyakrabban a CPU órájának aktuális ideje lesz.

A kvantumszámítógépek viszont valóban véletlenszerű számokat hozhatnak létre. Ennek az az oka, hogy a szuperpozícióban lévő qubit mérése valószínűségi folyamat. A mérés eredménye véletlenszerű, és nincs mód az eredmény előrejelzésére. Ez a kvantum véletlenszerű számgenerátorok alapelve.

A qubit a kvantuminformációk egysége, amely szuperpozícióban lehet. Méréskor a qubitek csak 0 vagy 1 állapotban lehetnek. A mérés előtt azonban a qubit állapota egy 0 vagy egy 1 méréssel való beolvasásának valószínűségét jelenti.

Először egy alapállapotú qubitet kell vennie, például nullát. A véletlenszerű számgenerátor első lépése egy Hadamard-művelettel egyenlő szuperpozícióba helyezni a qubitet. Ennek az állapotnak a mérése nulla vagy egy értéket eredményez, mindkettő 50%-os valószínűséggel, ezáltal egy igazán véletlenszerű bitet hozva létre.

Nem lehet tudni, hogy mit kap a qubit szuperpozícióban való mérése után, és az eredmény minden alkalommal más érték, amikor meghívja a kódot. De hogyan használhatja ezt a viselkedést nagyobb véletlenszerű számok létrehozására?

Tegyük fel, hogy négyszer ismétli meg a folyamatot, így az alábbi bináris számjegyet kapja:

$${0, 1, 1, 0}$$

Ha összefűzi vagy kombinálja ezeket a biteket egy bitsztringbe, akkor egy nagyobb számot kap. Ebben a példában a ${0110}$ bitsorozat decimális formában a 6-nak felel meg.

$${0110_{\ binary} \equiv 6_{\ decimal}}$$

Ha ezt a folyamatot többször is megismételi, több bitet is kombinálhat, hogy bármilyen nagy számot alkotjon. Ezzel a módszerrel létrehozhat egy számot, amelyet biztonságos jelszóként használhat, mivel biztos lehet abban, hogy egyetlen hacker sem tudja meghatározni a mérések sorozatának eredményeit.

A véletlenszám-generáló logikájának meghatározása

Vázoljuk fel a véletlenszerű számgenerátor logikáját:

Adja meg max a létrehozni kívánt maximális számot.
Adja meg a létrehozandó véletlenszerű bitek számát. Ez úgy történik, hogy kiszámítja, hány bitre van szüksége ahhoz, hogy az egészeket kifejezze max-ig.
Generáljunk egy nBits hosszúságú véletlenszerű bitsztringet.
Ha a bitsztring a max értékénél nagyobb szám, lépjünk vissza a harmadik lépéshez.
Ellenkező esetben a folyamat befejeződött. A létrehozott számot adjuk vissza egész számként.

Példaként állítsuk be a max értékét 12-re. Vagyis a 12 a legnagyobb szám, amelyet jelszóként szeretne használni.

${\lfloor ln(12) / ln(2) + 1 \rfloor}$, vagy 4 bitre van szüksége a 0 és 12 közötti szám megjelenítéséhez. Használhatjuk a beépített függvényt BitSizeI, amely bármilyen egész számot vesz igénybe, és visszaadja az annak megjelenítéséhez szükséges bitek számát.

Például hozzuk létre a ${1101_{\ binary}}$ bitsorozatot, ami megegyezik a ${13_{\ decimal}}$-lal. Mivel a 13 nagyobb mint 12, megismételjük a folyamatot.

Következő lépésként létrehozza az ${0110_{\ binary}}$ bites sztringet, amely egyenértékű a ${6_{\ decimal}}$-mal. Mivel a 6 kisebb mint 12, a folyamat befejeződött.

A kvantum véletlenszerű számgenerátor a 6-os számot adja vissza jelszóként. A gyakorlatban egy nagyobb számot állítson be maximális értékként, mert az alacsonyabb számok könnyen feltörhetőek az összes lehetséges jelszó kipróbálásával. Valójában a jelszó kitalálásának vagy feltörésének nehézségének növelése érdekében ASCII-kóddal konvertálhat binárisokat szöveggé, és számokat, szimbólumokat és vegyeses betűket használva hozhat létre jelszót.

Véletlenszerű bitgenerátort írjon meg

Az első lépés egy Q# véletlenszerű bitet generáló művelet írása. Ez a művelet a véletlenszerű számgenerátor egyik építőeleme lesz.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Most tekintse meg az új kódot.

Ön határozza meg a GenerateRandomBit műveletet, amely nem vesz fel bemenetet, és típusértéket Resulthoz létre. A Result típus egy mérés eredményét jelöli, és két lehetséges értékkel rendelkezhet: Zero vagy One.
Egyetlen qubitet foglal le a use kulcsszóval. A leosztáskor a qubitek mindig |0〉 állapotban lesznek.
A művelettel H a qubitet egyenlő szuperpozícióba helyezheti.
A művelettel M megmérheti a qubitet, visszaadhatja a mért értéket (Zero vagy One).
A művelettel Reset visszaállíthatja a qubitet a(z) |0〉 állapotba.

Ha a qubitet szuperpozícióba helyezi a H művelettel, és a művelettel M együtt méri, az eredmény minden alkalommal más érték, amikor a kód meghívása történik.

A kód vizualizációja Q# a Bloch-gömbdel

A Bloch-gömbön az északi pólus a 0 klasszikus értéket jelöli, a déli pólus pedig az 1 klasszikus értéket. Minden szuperpozíció megadható a gömb egyik pontjaként (ezt a nyíl jelzi). Minél közelebb van a nyíl hegye a pólushoz, annál nagyobb a valószínűsége, hogy a qubit a mérésekor a pólushoz hozzárendelt klasszikus értékkel esik egybe. Az alábbi ábrán látható nyíl által ábrázolt qubitállapot például nagyobb valószínűséggel ad 0 értéket, ha megméri.

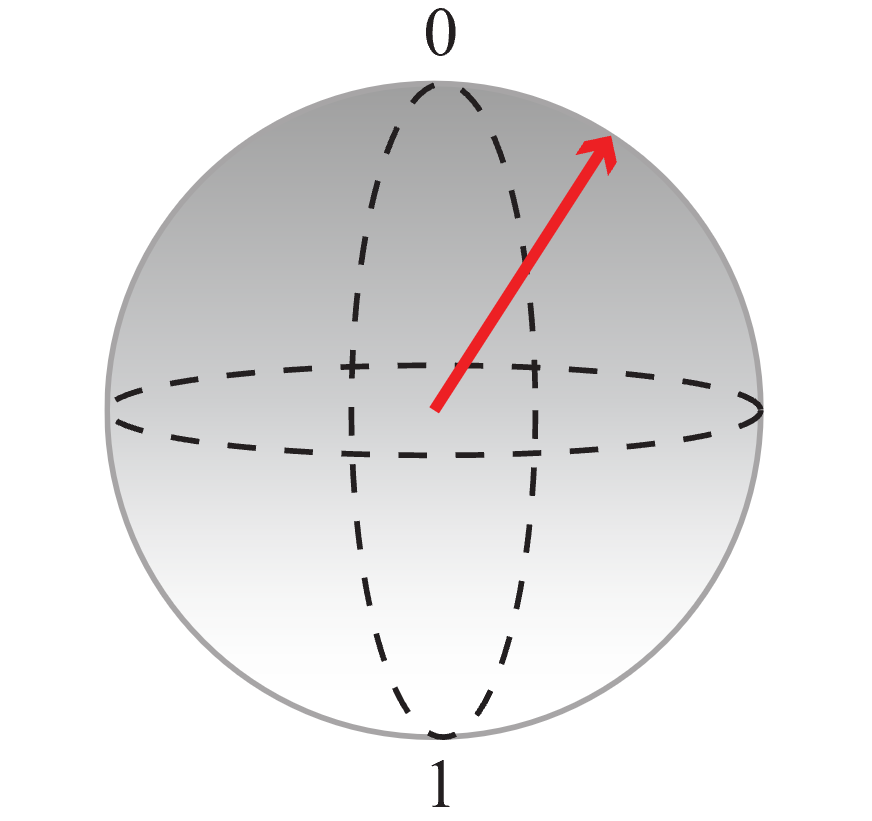
Egy olyan qubit állapotot ábrázoló diagram, amely nagy valószínűséggel méri a nullát.

Ezzel az ábrázolással megjelenítheti a kód műveletét:

Először kezdje a(z) |0〉 állapotban inicializált qubittel, és alkalmazzon egy műveletet egy H egyenlő szuperpozíció létrehozásához, amelyben a 0 és az 1 valószínűsége megegyezik.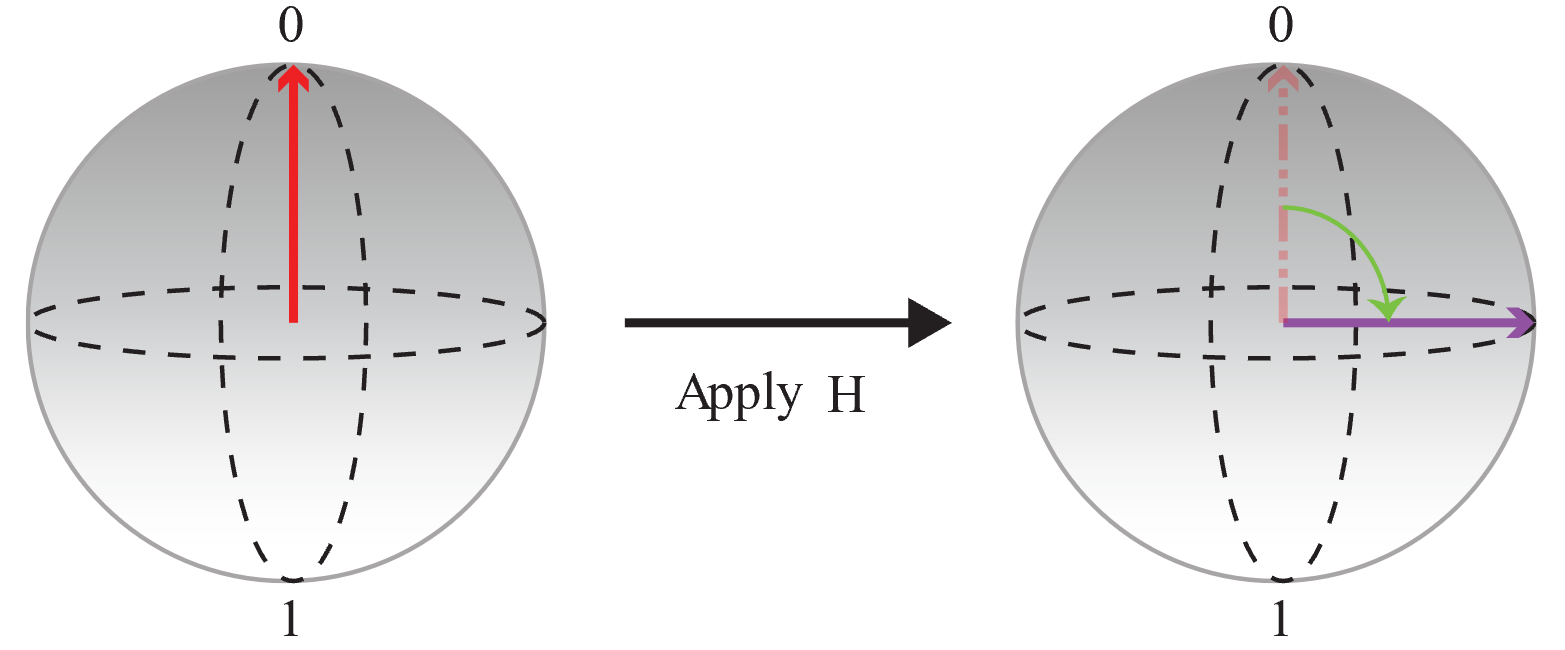
Ezután mérjük meg a qubitet, és mentsük a kimenetet:

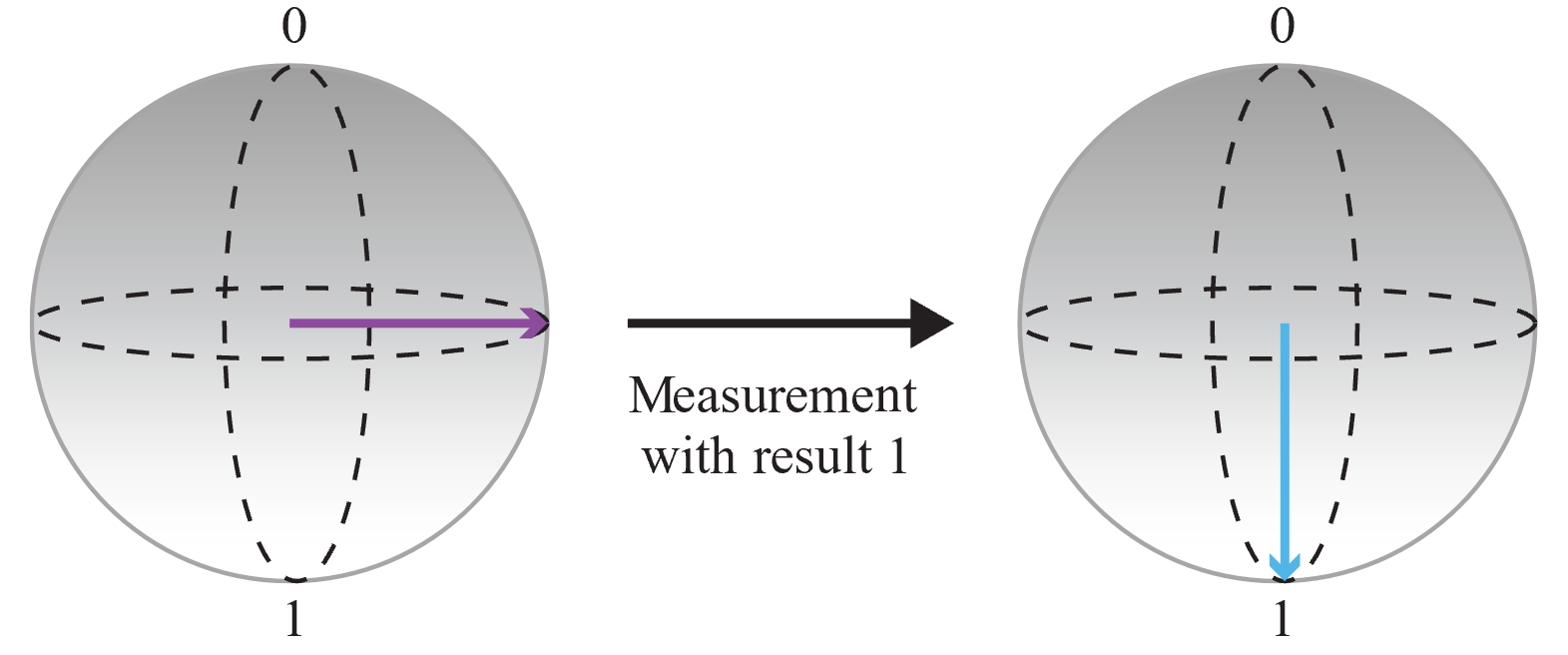
Mivel a mérés eredménye véletlenszerű, és a 0 és az 1 mérés valószínűsége megegyezik, teljesen véletlenszerű bitet kapott. Ezt a műveletet többször is meghívhatja egész számok létrehozásához. Ha például háromszor hívja meg a műveletet három véletlenszerű bit lekéréséhez, véletlenszerű 3 bites számokat hozhat létre (azaz 0 és 7 közötti véletlenszerű számot).

Teljes véletlenszerű számgenerátor írása

Először importálnia kell a szükséges névtereket a Q# standard kódtárból a programba. A Q# fordító sok gyakori függvényt és műveletet automatikusan betölt, azonban a teljes véletlenszerű számgenerátorhoz két Q# névtérből további függvényekre és műveletekre van szükség: Microsoft.Quantum.Mathés Microsoft.Quantum.Convert.
```
import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;
```
Ezután határozza meg a GenerateRandomNumberInRange műveletet. Ez a művelet többször meghívja a GenerateRandomBit műveletet a bitek sztringjének létrehozásához.
```
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}
```
Most vizsgáljuk meg az új kódot.
- Ki kell számítania, hogy hány bit szükséges az egész számok kifejezéséhez legfeljebb max. A BitSizeI névtérből származó Microsoft.Quantum.Math függvény egy egész számot a reprezentáláshoz szükséges bitek számává alakít át.
- A SampleRandomNumberInRange művelet egy for hurkot használ arra, hogy véletlenszerű számokat generáljon egészen addig, amíg az kisebb vagy egyenlő nem lesz a max értékével. A for hurok pontosan ugyanúgy működik, mint a for ciklusok más programozási nyelvekben.
- A változó bits egy módosítható változó. A módosítható változó olyan, amely változhat a számítás közben. Ennek a módosítható változónak a módosításához a set direktívát használjuk.
- A ResultArrayAsInt függvény az alapértelmezett Microsoft.Quantum.Convert névtérből pozitív egész számmá alakítja a bitsztringet.
Végül hozzáad egy belépési pontot a programhoz. Alapértelmezés szerint a Q# fordító a Main műveletet keresi meg, és ott kezdi el a feldolgozást. Meghívja a GenerateRandomNumberInRange műveletet, hogy véletlenszerű számot hozzon létre 0 és 100 között.
```
operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}
```
A let direktíva olyan változókat deklarál, amelyek nem változnak a számítás során. Itt a maximális értéket 100-ként definiálja.

A művelettel kapcsolatos további információkért lásd: Main Belépési pontok.
A véletlenszerű számgenerátor teljes kódja a következő:

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using a Hadamard operation
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

A véletlenszerű számgenerátor program futtatása

A programot futtathatja a Copilotban az Azure Quantumban, a Visual Studio Code-ban pedig önálló Q# alkalmazásként vagy Python-gazdagépprogram használatával.

A Q# kódot ingyenesen tesztelheti a Copilottal az Azure Quantumban – mindössze egy Microsoft (MSA) e-mail-fiókra van szüksége. Az Azure Quantum Copilot-járól további információt az Azure Quantum felfedezése című témakörben talál.

Nyissa meg a Copilotot az Azure Quantumban a böngészőben.

Másolja és illessze be a következő kódot a kódszerkesztőbe.

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Válassza ki a futtatandó lövések számát, és válassza a Futtatás lehetőséget.
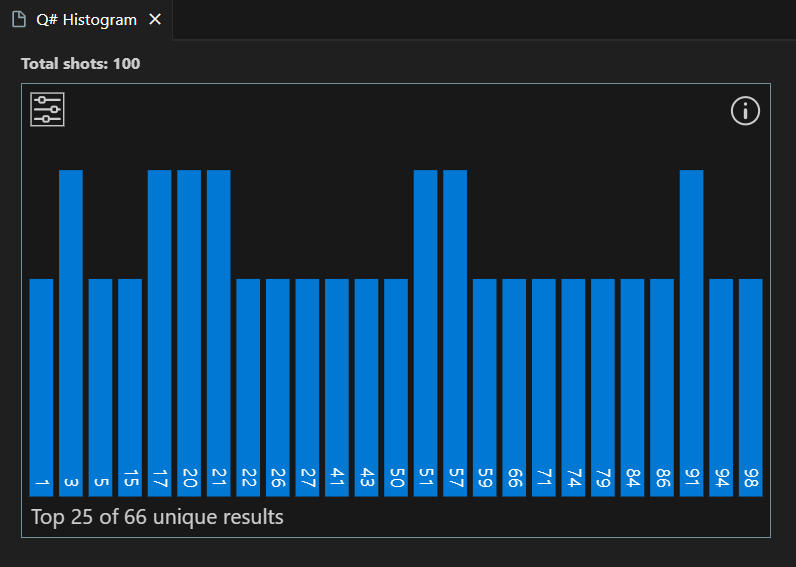
Az eredmények a hisztogramban és az Eredmények mezőkben jelennek meg.
A Kód magyarázata lehetőséget választva kérje meg a Copilototot, hogy magyarázza el Önnek a kódot.

Tipp.

Az Azure Quantum Copilotjából megnyithatja programját a webes VS Code-ban azáltal, hogy a kódszerkesztő jobb sarkában található VS Code emblémára kattint.

Nyissa meg a Visual Studio Code-ot, és válassza a Fájl > új szövegfájlja lehetőséget egy új fájl létrehozásához.
Mentse a fájlt RandomNumberGenerator.qs néven. Ez a fájl tartalmazza a Q# program kódját.

Másolja a következő kódot a RandomNumberGenerator.qs fájlba.


import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

A program futtatása előtt a profilt korlátlantargetkell állítania. Válassza a Nézet – Parancspaletta lehetőséget, keressen rá a QIR-ra, válassza a Azure Quantum QIR profil beállítása, majd válassza az korlátlan lehetőséget.
A program futtatásához válassza a Futtatás Q# Fájl opciót a lejátszás ikon jobb felső részén található lenyíló menüből, válassza ki a Futtatás opciót a parancsok listájából, vagy nyomja meg a Ctrl+F5 billentyűkombinációt. A program az Main() alapértelmezett szimulátoron futtatja a műveletet.
A kimenet megjelenik a hibakeresési konzolon.
Futtassa újra a programot egy másik eredmény megjelenítéséhez.

Feljegyzés

Ha a target profil nincs korlátozás nélkül beállítva, akkor hibaüzenet jelenik meg a program futtatásakor.

A frekvencia hisztogram ábrázolása

Vizualizáljuk a kvantumprogram többszöri futtatásából nyert eredmények eloszlását. A gyakorisági hisztogram segít ezeknek az eredményeknek a valószínűségi eloszlásának megjelenítésében.

Válassza a Nézet –> Parancs paletta lehetőséget, és írja be a "hisztogram" kifejezést, amely megjeleníti a Q# Fájl futtatása és hisztogram megjelenítése opciót. A Hisztogram parancsot is kiválaszthatja a Main() előtti parancsok listájából. Ezzel a beállítással megnyithatja a Q# hisztogramablakot.
Adjon meg egy bizonyos számú lövést a program végrehajtásához, például 100 lövést, majd nyomja meg az Enter gombot. A hisztogram megjelenik a Q# hisztogram ablakban.
A hisztogram minden sávja egy lehetséges eredménynek felel meg, magassága pedig az eredmény megfigyelésének hányszorosát jelöli. A különböző eredmények száma a hisztogram minden futtatásakor eltérő lehet.

Tipp.

A hisztogramot az egér görgetőkerekével vagy egy trackpad-kézmozdulattal nagyíthatja. Nagyításkor görgetés közben az "Alt" billentyű lenyomásával pásztázhatja a diagramot.
Jelöljön ki egy sávot az eredmény százalékos arányának megjelenítéséhez.
A beállítások megjelenítéséhez válassza a bal felső beállítások ikont . Megjelenítheti az első 10 találatot, a 25 legjobb eredményt vagy az összes találatot. Az eredményeket a magasról az alacsonyra vagy az alacsonyról a magasra is rendezheti.

A VS Code-ban válassza a Nézet> Parancspaletta lehetőséget, majd a Létrehozás: Új Jupyter-jegyzetfüzet opciót.
Az első cellában importálja a csomagot a qsharp Python-kódba:
```
import qsharp
```

Adja hozzá a Q# kvantum véletlenszám-generátor program kódját. Ehhez használja a %%qsharp mágikus parancsot. Vegye figyelembe, hogy a %%qsharp parancs a jegyzetfüzet cellájának típusát Python-ról Q#-ra módosítja. Másolja a kódot a második cellába.

%%qsharp

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

Végül futtassa a kódot. Ugyanazt a szimulációt több alkalommal is futtathatja egymástól függetlenül. Minden független szimulációt "lövésnek" nevezünk. Például futtassuk le a szimulációt 100-szor.
```
results = qsharp.run("Main()", shots=100)
print(results)
```

Feljegyzés

Ez a kódrészlet jelenleg nem fut elérhető Azure Quantum-hardverentargets, mivel a hívhatóhoz ResultArrayAsInt teljes számítási profillal rendelkező QPU szükséges.

További Q# oktatóanyagok:

A kvantum-összefonódás bemutatja, hogyan írhat olyan Q# programot, amely manipulálja és méri a qubiteket, és bemutatja a szuperpozíció és az összefonódás hatásait.
A Grover keresési algoritmusa bemutatja, hogyan írhat olyan Q# programot, amely a Grover keresési algoritmusát használja.
A Quantum Fourier Transforms bemutatja, hogyan írhat olyan Q# programot, amely közvetlenül kezeli az adott qubiteket.
A Quantum Katas öngyors oktatóanyagok és programozási gyakorlatok, amelyek célja a kvantum-számítástechnika és Q# a programozás elemeinek egyidejű tanítása.

Megosztás a következőn keresztül: