Gépi tanulási modellek eredményei

Ez a cikk a mátrixok félreértését, osztályozási problémákat és a gépi tanulás (FOG) modelljeinek pontosságát tárgyalja. Az a cél, hogy jobban megértsék az ML előrejelzési eredményeinek pontosságát. A célközönség olyan mérnökök, elemzők és vezetők, akik szeretnék fejleszteni tudásukat és szakértelmüket az adattudomány terén.

Zavartság-mátrix

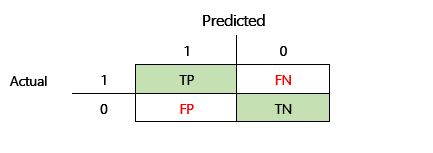
Miután a felügyelt ML-es problémát az előzményadatok egy csoportján képezik, a teszt a képzési folyamatból visszatartott adatok alapján történik. Így összevetheti a képzett modell előrejelzéseit a tényleges értékekkel. A zavartság-mátrix meghatározza, hogy milyen sikeresek az osztályozási problémák, és hogy hol vét hibákat (azaz hol „zavaros”).

Például az a cél, hogy valamilyen fizikai és viselkedési tulajdonság alapján megjósolja, hogy egy adott állat éppen kutya vagy macska. Ha van egy tesztadathalmaz, ami 30 kutyát és 20 macskát tartalmaz, akkor a zavartság-mátrix a következő illusztrációra hasonlíthat.

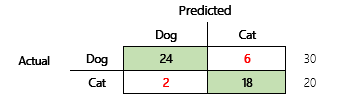
A zöld cellákban szereplő számok helyes előrejelzéseket jelentenek. Amint látható, a modell a tényleges macskák számánál magasabb százalékban jósolt helyesen macskákat. A modell teljes pontossága könnyen kiszámítható. Ebben az esetben 42 ÷ 50 vagy 0,84.

Többosztályos osztályozók a zavartság-mátrixban

A zavartság-mátrixra vonatkozó legtöbb vitát a bináris osztályozók határozzák meg, mint az előző példában. Ez egy olyan speciális eset, amikor más metrikák is megtekinthetők, például az érzékenység és a visszahívás.

Ezután fontolóra vesszük egy olyan finanszírozási eset osztályozási problémáját, amelynek három szakasza van. A modell azt jelzi, hogy a vevői számlát időben, késve vagy nagyon későn fizetik ki. Például a 100 tesztszámlából 50 kerül kifizetésre időben, 35 későn, 15 pedig nagyon későn. Ebben az esetben előfordulhat, hogy egy modell zavartság-mátrixot hoz létre, amely a következő illusztrációhoz hasonlít.

]

A zavartság-mátrix jóval több adatot tartalmaz, mint egy egyszerű pontossági metrika. Ezt azonban aránylag könnyű megérteni. A zavartság-mátrix azt jelzi, hogy van-e olyan kiegyensúlyozott adathalmaz, amelyben a kimeneti osztályok hasonló számokkal rendelkeznek. A többosztályos forgatókönyv azt jelzi, hogy milyen messze van az előrejelzés, ha a kimeneti osztályok sorban vannak, mint a vevői kifizetésekkel kapcsolatos előző példában.

Modell pontossága

A különböző pontossági metrikák előnye, hogy számszerűsítik a modell minőségét.

Mivel a pontosság egy könnyű metrika, így jó kiindulási pont, amellyel elmagyarázható a modell más személyek számára, különösen azoknak a modelleknek a felhasználói számára, akik nem adatszakértők. A modell pontosságának megértéséhez nem szükséges a statisztikai adatok megértése. Ha rendelkezésre áll egy zavartság-mátrix, további betekintést nyújt a modell teljesítményéhez.

Alaposabb megértés érdekében azonban több, a pontossághoz kapcsolódó kihívást kell megfigyelni. A metrika hasznossága a probléma környezetén múlik. A modell teljesítményével kapcsolatban gyakran az a kérdés, hogy mennyire jó a modell? A kérdésre adott válasz azonban nem feltétlenül egyértelmű. Vegye figyelembe a következő zavartság-mátrixot (2. modell).

Egy gyors számítás azt jelzi, hogy a modell pontossága (70 + 10 + 3) ÷ 100 vagy 0,83. A felszínen ez az eredmény jobbnak tűnik, mint az előző többosztályos modell (1. modell) eredménye, amelynek pontossága 0,73. De jobb-e?

A kérdés elkezdéséhez a naiv becslés pontosságát kell figyelembe venni. Az osztályozási probléma esetében az egyszerű becslés mindig a legáltalánosabb osztályt fogja megjósolni. Az 1. modell esetében a becslés „időben”, és 0,50 pontossággal fog elkészülni. A 2. modell esetében is „időben” lesz a becslés, és 0,80 pontossággal fog elkészülni. Mivel az 1. modell tökéletesíti a naiv becslést 0,73 – 0,50 = 0,23-mal, míg a 2. modell tökéletesíti a naiv becslést a 0,83 – 0,80 = 0,03-mal, az 1. modell egy jobb modell, még akkor is, ha kisebb a pontossága. A számítás azt mutatja, hogy a modell minőségi értékelésének a pontossági értéknél nagyobbnak kell lennie.

Egy másik szempontot is érdemes megjegyezni. Gondoljon egy olyan forgatókönyvre, amikor egy orvosi tesztet használnak egy páciens betegségének kimutatására. Ez a probléma egy bináris besorolási probléma, ahol a pozitív eredmény azt jelzi, hogy a páciens beteg. Ebben a forgatókönyvben a következő hibák hatásait kell megfontolni:

• Hamis pozitív, amikor a teszt azt mutatja, hogy a páciens beteg, de valójában nem is az.
• Hamis negatív, amikor a teszt azt mutatja, hogy a páciens nem beteg, de valójában az.

Nyilvánvalóan egy típusú hiba sem kívánatos, de melyik a rosszabb? Ez ismét a helyzettől függ. Abban az esetben, ha egy életveszélyes betegség gyors kezelést igényel, a hamis negatívok minimalizálása (remélhetőleg további teszteket is elvégeznek) élvez prioritást. Más, kevésbé kritikus helyzetek esetén a modell létrehozói csökkenthetik a hamis pozitív értéket. Egy észszerű következtetés szerint a modell minőségi meghatározásához több információra van szükség, mint a pontossági metrika.

Javaslatok

A pontosság fontos eszköz a statisztikai adatokat nem ismerő tartományszakértőkkel történő kommunikációra. Ahhoz azonban, hogy az adatok hasznosak legyenek, kritikus, hogy a pontossági értékkel együtt további kontextust biztosítsanak.

A kifizetés előrejelzési esetéhez beállíthatja egy ML-modell célt, amely tényezőket tartalmaz a különböző fizetési módokban. A cél az, hogy a modell tökéletesítse a naiv becslést a helytelen válaszok számának legalább 50 százalékos csökkentésével. Más szóval azt szeretné, hogy a cél pontossága elossza a különböző pontosságot a naiv becslés és a 100 százalék között.

Az alábbi táblázat összefoglalja ezt az elvet a cikk félreértések mátrixai miatt.

Típus	Naiv becslés	Cél	Modell pontossága	Megfelel a célnak?
1. modell	0.50	0.75	0.73	Majdnem. Ez a modell jelentősen javítja a becslést.
2. modell	0.80	0.90	0.83	Szám Javításra van szükség.

F1-es osztályozás pontossága

A végső szempont ebben a cikkben a MÁS NÉVEN F1 pontosságú besorolás teljesítményének egy speciális mértéke.

Az F1 pontosság meghatározása előtt két további metrikát kell bevezetni: precizitás és visszahívás. A precizitás azt jelzi, hogy a pozitívként megadott előrejelzések számának hány százalékát rendeli hozzá helyesen a program. Ez a metrika pozitív előrejelző-értékként is ismert. A visszahívás azon tényleges pozitív esetek teljes száma, amelyeket helyesen jósoltak meg. Ez a metrika más néven érzékenység.

Az előző ábrán látható zavartság-mátrixban a program a következő módon számította ki a metrikákat:

• Pontosság = TP ÷ (TP + FP)
• Visszahívás = TP ÷ (TP + FN)

Az F1-mérték ötvözi a precizitást és a visszahívást. Az eredmény a két érték harmonikus átlaga. A számítás a következőképpen történik:

• F1 = 2 × (precízió × visszahívás) ÷ (precízió + visszahívás)

Nézzünk meg egy konkrét példát. A cikk korábbi része egy olyan modellre példa, amely előrejelzést ad arról, hogy egy új verzió vagy egy cat volt-e. A program itt ismétli meg az ábrát.

Ezek az eredmények, ha a „kutya” a pozitív válasz.

• Pontosság = 24 ÷ (24 + 2) = 0,9231
• Visszahívás = 24 ÷ (24 + 6) = 0,8
• F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572

Amint látható, az F1 érték a pontosság és a visszahívás értékei között szerepel.

Bár az F1 pontosságát nem könnyű megérteni, árnyaltságot ad az alapszintű pontossági számnak. Ezenkívül segíthet a kiegyenlítetlen adathalmazok esetében is, ahogy azt a következő beszélgetés is mutatja.

A cikk Modell pontossági szakasza összehasonlította a következő két félreértési mátrixot. Annak ellenére, hogy az első modellnél alacsonyabb a pontosság, hasznosabb modellnek tekintették, mivel nagyobb javulást mutatott, mint a határidős fizetés alapértelmezett becslése.

Lássuk, hogyan lehet összehasonlítani ezt a két modellt az F1-es pontszám használatakor. Az F1-es pontszám a pontosság és az egyes állapotok visszahívása, az F1-es makroszámítás pedig az F1-es pontszám átlagát határozza meg az egyes állapotokban az F1-es pontszám átfogó meghatározásához. Más F1-es változatok is léteznek, de érdekesebb a makroverzió megfontolása, alapul véve mindhárom állapotban megadott egyenlő mértékű odafigyelést.

A számítások egyszerűsítése érdekében a mintatömböket úgy építették, hogy megfeleljenek a tényleges és az előrejelzett értékeknek. Ezek a tömbök a Pythonban a sklearn metrikáját használják az értékek kiszámításához. Az eredmény a következő.

Típus	Naiv becslés	Pontosság	F1 makró
1. modell	0.5	0.73	0.67
2. modell	0.80	0.83	0.66

A számítás működésével kapcsolatos további részleteket a sklearn.metrics osztályozási jelentés az 1. modellhez részben talál. A három „Időben”, „Későn” és „Nagyon későn” állapotot az 1., 2. és 3. címkével ellátott sorok jelölik. A makró átlaga csak az „f1-pontszám” oszlop átlaga.

	pontosság	visszahívás	f1-pontszám
1	0.83	0.80	0.82
2	0.68	0.71	0.69
3	0.50	0.50	0.50

Ezek az eredmények azt mutatják, hogy a két modellhez közel azonos F1-es makrópontossági pontszám tartozik. Ebben és sok más esetben az F1 pontossága jobban jelzi a modell képességeit. A pontosság érdekében az eredmények értelmezése megköveteli, hogy a modellben figyelembe vegyék a legfontosabb tényezőt.