Polygon

A következőkre vonatkozik:SQL Server Azure SQL Database Felügyelt Azure SQL-példány SQL Analytics-végpont a Microsoft Fabricben Raktár a Microsoft Fabricben SQL-adatbázis a Microsoft Fabricben

A sokszög egy kétdimenziós felület, amely pontok sorozataként van tárolva, amelyek egy külső határoló gyűrűt és nulla vagy több belső gyűrűt határoznak meg.

Sokszögpéldányok

A sokszögpéldányok olyan gyűrűből hozhatók létre, amely legalább három különböző ponttal rendelkezik. A sokszögpéldány is lehet üres.

A poligon külső és belső gyűrűi határozzák meg a határait. A gyűrűkben lévő tér határozza meg a poligon belsejét.

Az alábbi ábrán a sokszögpéldányok példái láthatók.

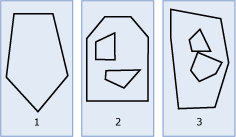
Példák geometriai sokszögpéldányokra.

Ahogy az ábrán látható:

Az 1. ábra egy olyan sokszögpéldány , amelynek határát egy külső gyűrű határozza meg.
A 2. ábra egy olyan sokszögpéldány , amelynek határát egy külső gyűrű és két belső gyűrű határozza meg. A belső gyűrűk által határolt terület a Sokszög példány külső részéhez tartozik.
A 3. ábra egy érvényes sokszögpéldány , mivel belső gyűrűi egyetlen érintőponton metszik egymást.

Elfogadott példányok

Az elfogadott sokszögpéldányok olyan példányok, amelyek egy geometriai vagy földrajzi változóban tárolhatók kivétel nélkül. A következők elfogadott Polygon példányok:

Üres sokszögpéldány
Olyan sokszög-példány, amelynek elfogadható külső gyűrűje (LineString) és nulla vagy több elfogadható belső gyűrűje (LineString) van.

Az alábbi feltételek szükségesek ahhoz, hogy egy gyűrű (LineString) elfogadható legyen.

A LineString-példányt el kell fogadni.
A LineString-példánynak legalább négy ponttal kell rendelkeznie.
A LineString-példány kezdő és záró pontjainak meg kell egyeznie.

Az alábbi példa az elfogadott sokszögpéldányokat mutatja be.

DECLARE @g1 geometry = 'POLYGON EMPTY';  
DECLARE @g2 geometry = 'POLYGON((1 1, 3 3, 3 1, 1 1))';  
DECLARE @g3 geometry = 'POLYGON((-5 -5, -5 5, 5 5, 5 -5, -5 -5),(0 0, 3 0, 3 3, 0 3, 0 0))';  
DECLARE @g4 geometry = 'POLYGON((-5 -5, -5 5, 5 5, 5 -5, -5 -5),(3 0, 6 0, 6 3, 3 3, 3 0))';  
DECLARE @g5 geometry = 'POLYGON((1 1, 1 1, 1 1, 1 1))';

Előfordulhat, hogy ahogyan a @g4 és @g5 mutatja, egy elfogadott Polygon példány nem érvényes Polygon példány. @g5 azt is jelzi, hogy a sokszögpéldánynak csak egy bármely négy pontból álló gyűrűt kell tartalmaznia.

Az alábbi példák System.FormatException-t váltanak ki, mivel a Polygon példányok nem elfogadhatók.

DECLARE @g1 geometry = 'POLYGON((1 1, 3 3, 1 1))';  
DECLARE @g2 geometry = 'POLYGON((1 1, 3 3, 3 1, 1 5))';

@g1 nem fogadható el, mert a külső gyűrű LineString-példánya nem tartalmaz elegendő pontot. @g2 nem fogadható el, mert a külső gyűrű LineString-példányának kezdőpontja nem ugyanaz, mint a végpont. Az alábbi példa egy elfogadható külső gyűrűvel rendelkezik, de a belső gyűrű nem elfogadható. Ez szintén kivált egy System.FormatException.

DECLARE @g geometry = 'POLYGON((-5 -5, -5 5, 5 5, 5 -5, -5 -5),(0 0, 3 0, 0 0))';

Érvényes példányok

A sokszög belső gyűrűi egyetlen érintőponton érinthetik egymást és önmagukat is, de ha a sokszög belső gyűrűi átmetszik egymást, akkor a példány nem érvényes.

Az alábbi példa érvényes sokszögpéldányokat mutat be.

DECLARE @g1 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20))';  
DECLARE @g2 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0))';  
DECLARE @g3 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0), (-10 0, 0 10, -5 -10, -10 0))';  
SELECT @g1.STIsValid(), @g2.STIsValid(), @g3.STIsValid();

@g3 azért érvényes, mert a két belső gyűrű egyetlen ponton érintkezik, és nem keresztezik egymást. Az alábbi példa az érvénytelen Polygon példányokat mutatja be.

DECLARE @g1 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (20 0, 0 10, 0 -20, 20 0))';  
DECLARE @g2 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0), (5 0, 1 5, 1 -5, 5 0))';  
DECLARE @g3 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0), (-10 0, 0 10, 0 -10, -10 0))';  
DECLARE @g4 geometry = 'POLYGON((-20 -20, -20 20, 20 20, 20 -20, -20 -20), (10 0, 0 10, 0 -10, 10 0), (-10 0, 1 5, 0 -10, -10 0))';  
DECLARE @g5 geometry = 'POLYGON((10 0, 0 10, 0 -10, 10 0), (-20 -20, -20 20, 20 20, 20 -20, -20 -20) )';  
DECLARE @g6 geometry = 'POLYGON((1 1, 1 1, 1 1, 1 1))';  
SELECT @g1.STIsValid(), @g2.STIsValid(), @g3.STIsValid(), @g4.STIsValid(), @g5.STIsValid(), @g6.STIsValid();

@g1 érvénytelen, mert a belső gyűrű két helyen érinti a külső gyűrűt. @g2 érvénytelen, mert a második belső gyűrű az első belső gyűrű belsejében található. @g3 érvénytelen, mert a két belső gyűrű több egymást követő ponton érintkezik. @g4 érvénytelen, mert a két belső gyűrű belső részei átfedésben vannak. @g5 érvénytelen, mert nem a külső gyűrű az első gyűrű. @g6 érvénytelen, mert a gyűrűnek nincs legalább három különböző pontja.

Térbeli adatok tájolása

A sokszög gyűrű tájolása nem fontos tényező a síkrendszerben. Az SQL-specifikáció egyszerű OGC-funkciói nem szabják meg a gyűrűk sorrendjét, és az SQL Server nem kényszeríti a gyűrűrendezést.

A három pontrendszerben a tájolás nélküli sokszögnek nincs jelentése, vagy nem egyértelmű. Az egyenlítő körüli gyűrű például az északi vagy a déli féltekét írja le? Ha a térbeli példány tárolásához a földrajzi adattípust használjuk, meg kell határoznunk a gyűrű tájolását, és pontosan le kell írnunk a példány helyét.

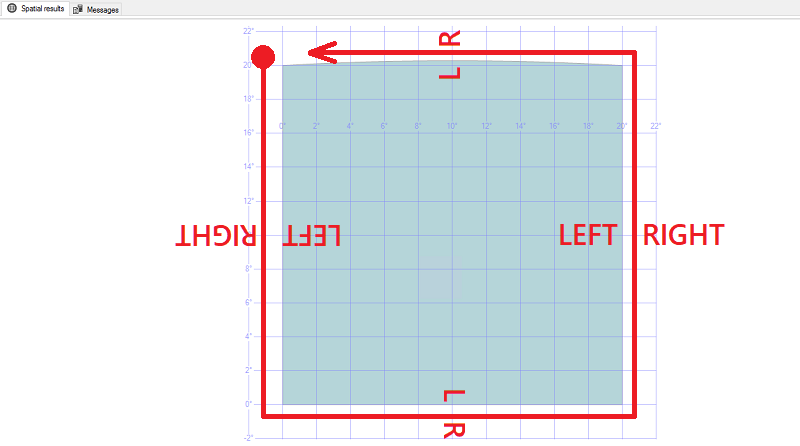
A három pontrendszerben lévő sokszög belsejét a "bal oldali szabály" határozza meg: ha azt képzeli, hogy egy földrajzi sokszög gyűrűje mentén sétál, követve a pontokat a felsorolás sorrendjében, a bal oldali területet a poligon belső részének, a jobb oldali területet pedig a Poligon külső részének tekintik.

Az óramutató járásával ellentétes irányban

DECLARE @square GEOGRAPHY;
SET @square = GEOGRAPHY::STPolyFromText('POLYGON((0 20, 0 0, 20 0, 20 20, 0 20))', 4326);
SELECT @square;

Óramutató járásával megegyező irányban

DECLARE @square GEOGRAPHY;
SET @square = GEOGRAPHY::STPolyFromText('POLYGON((0 20, 20 20, 20 0, 0 0, 0 20))', 4326);
SELECT @square;

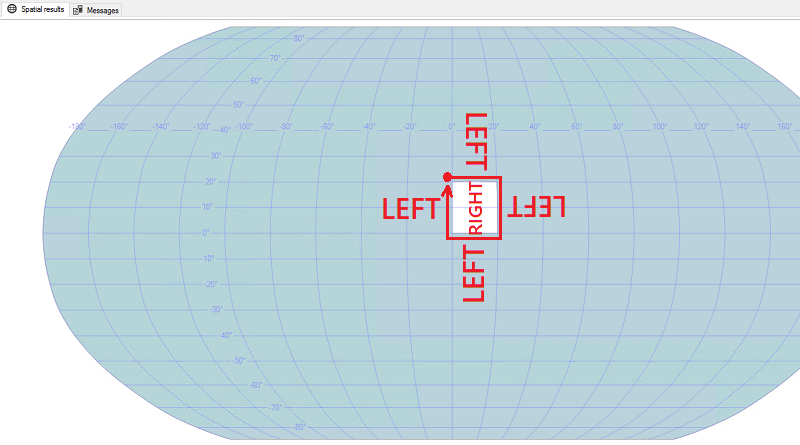
Ha az SQL Server kompatibilitási szintje 100 vagy annál alacsonyabb, a földrajzi adattípusra az alábbi korlátozások vonatkoznak:

Minden földrajzi példánynak egyetlen féltekén belül kell elférnie. A félgömbnél nagyobb térbeli objektumok nem tárolhatók.
Az Open Geospatial Consortium (OGC) Well-Known Text (WKT) vagy Well-Known Bináris (WKB) ábrázolás bármely olyan földrajzi példánya, amely egy félgömbnél nagyobb objektumot hoz létre, argumentumException értéket ad.
A két földrajzi példány (például STIntersection(), , STUnion(), STDifference()és STSymDifference()) bemenetét igénylő földrajzi adattípus-metódusok null értéket adnak vissza, ha a metódusok eredményei nem férnek el egyetlen féltekén belül. STBuffer() null értéket is ad vissza, ha a kimenet meghaladja az egyetlen féltekét.

A tájolás megfordítható a ReorientObject (földrajzi adattípus) kiterjesztett metódus használatával.

Examples

A. példa.

Az alábbi példa egy egyszerű geometry Polygon példányt hoz létre, amely egy rést és egy SRID 10-et eredményez.

DECLARE @g geometry;  
SET @g = geometry::STPolyFromText(
    'POLYGON((0 0, 0 3, 3 3, 3 0, 0 0), (1 1, 1 2, 2 1, 1 1))',
    10);

B. példa.

Érvénytelen példányok beírhatók és átalakíthatók érvényes geometry példánysá. Az alábbi példában a Polygon belső és külső gyűrűk átfedik egymást, és a példány nem érvényes.

DECLARE @g geometry;  
SET @g = geometry::Parse(
    'POLYGON((1 0, 0 1, 1 2, 2 1, 1 0), (2 0, 1 1, 2 2, 3 1, 2 0))'
    );

C. példa.

Az alábbi példában az érvénytelen példány érvényessé lett téve a következővel MakeValid(): .

SET @g = @g.MakeValid();  
SELECT @g.ToString();

Az geometry előző példából visszaadott példány egy MultiPolygon.

MULTIPOLYGON (((2 0, 3 1, 2 2, 1.5 1.5, 2 1, 1.5 0.5, 2 0)),
              ((1 0, 1.5 0.5, 1 1, 1.5 1.5, 1 2, 0 1, 1 0)))

D. példa.

Ez egy másik példa egy érvénytelen példány érvényes geometriai példánysá alakítására. Az alábbi példában a Polygon példány három ponttal lett létrehozva, amelyek pontosan megegyeznek:

DECLARE @g geometry  
SET @g = geometry::Parse('POLYGON((1 3, 1 3, 1 3, 1 3))');  
SET @g = @g.MakeValid();  
SELECT @g.ToString()

A korábban visszaadott geometriapéldány egy Point(1 3). Ha a Polygon adott, akkor a POLYGON((1 3, 1 5, 1 3, 1 3))MakeValid() vissza fog térni LINESTRING(1 3, 1 5).

Visszajelzés

Hasznosnak találta ezt az oldalt?

Last updated on 2025-11-18