Berbagai cara untuk menjalankan Estimator Sumber Daya
Dalam artikel ini, Anda belajar bekerja dengan Azure Quantum Resource Estimator. Estimator Sumber Daya adalah bagian dari Quantum Development Kit dan tersedia di berbagai platform dan IDEs.
Jika Anda menjalankan program Q#, Estimator Sumber Daya tersedia di Visual Studio Code dengan ekstensi Quantum Development Kit. Anda tidak neet untuk memiliki langganan Azure untuk menggunakan Estimator Sumber Daya di Visual Studio Code.
Jika Anda menjalankan program Qiskit atau QIR, Estimator Sumber Daya tersedia di portal Azure, dan Anda memerlukan langganan Azure untuk menggunakannya.
Tabel berikut ini memperlihatkan berbagai cara untuk menjalankan Estimator Sumber Daya.
| Skenario Pengguna | Platform | Tutorial |
|---|---|---|
| Memperkirakan sumber daya program Q# | Visual Studio Code | Pilih Q# di Visual Studio Code di bagian atas halaman |
| Memperkirakan sumber daya program Q# (tingkat lanjut) | Jupyter Notebook di Visual Studio Code | Pilih Q# di Jupyter Notebook di bagian atas halaman |
| Memperkirakan sumber daya program Qiskit | Portal Azure | Pilih Qiskit di portal Azure di bagian atas halaman |
| Memperkirakan sumber daya program QIR | Portal Azure | Kirim QIR |
| Gunakan file FCIDUMP sebagai parameter argumen (tingkat lanjut) | Visual Studio Code | Mengirimkan masalah kimia kuantum |
Prasyarat untuk Visual Studio Code
- Versi terbaru Visual Studio Code atau buka VISUAL Code di Web.
- Versi terbaru ekstensi Azure Quantum Development Kit. Untuk detail penginstalan, lihat Menginstal QDK di Visual Studio Code.
Tip
Anda tidak perlu memiliki akun Azure untuk menjalankan Estimator Sumber Daya lokal.
Membuat file Q# baru
- Buka Visual Studio Code dan pilih File > Teks Baru untuk membuat file baru.
- Simpan file sebagai
ShorRE.qs. File ini akan berisi kode Q# untuk program Anda.
Membuat algoritma kuantum
Salin kode berikut ke dalam file ShorRE.qs:
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;
operation Main() : Unit {
let bitsize = 31;
// When choosing parameters for `EstimateFrequency`, make sure that
// generator and modules are not co-prime
let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}
// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.
/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
generator : Int,
modulus : Int,
bitsize : Int
)
: Int {
mutable frequencyEstimate = 0;
let bitsPrecision = 2 * bitsize + 1;
// Allocate qubits for the superposition of eigenstates of
// the oracle that is used in period finding.
use eigenstateRegister = Qubit[bitsize];
// Initialize eigenstateRegister to 1, which is a superposition of
// the eigenstates we are estimating the phases of.
// We first interpret the register as encoding an unsigned integer
// in little endian encoding.
ApplyXorInPlace(1, eigenstateRegister);
let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
// Use phase estimation with a semiclassical Fourier transform to
// estimate the frequency.
use c = Qubit();
for idx in bitsPrecision - 1..-1..0 {
within {
H(c);
} apply {
// `BeginEstimateCaching` and `EndEstimateCaching` are the operations
// exposed by Azure Quantum Resource Estimator. These will instruct
// resource counting such that the if-block will be executed
// only once, its resources will be cached, and appended in
// every other iteration.
if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
Controlled oracle([c], (1 <<< idx, eigenstateRegister));
EndEstimateCaching();
}
R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
}
if MResetZ(c) == One {
set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
}
}
// Return all the qubits used for oracles eigenstate back to 0 state
// using Microsoft.Quantum.Intrinsic.ResetAll.
ResetAll(eigenstateRegister);
return frequencyEstimate;
}
/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
// The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
// also use `ExpModI` to compute a by which x must be multiplied. Also
// note that we interpret target as unsigned integer in little-endian
// encoding.
ModularMultiplyByConstant(modulus,
ExpModI(generator, power, modulus),
target);
}
/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
use qs = Qubit[Length(y)];
for (idx, yq) in Enumerated(y) {
let shiftedC = (c <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
}
ApplyToEachCA(SWAP, Zipped(y, qs));
let invC = InverseModI(c, modulus);
for (idx, yq) in Enumerated(y) {
let shiftedC = (invC <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
}
}
/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
body (...) {
Controlled ModularAddConstant([], (modulus, c, y));
}
controlled (ctrls, ...) {
// We apply a custom strategy to control this operation instead of
// letting the compiler create the controlled variant for us in which
// the `Controlled` functor would be distributed over each operation
// in the body.
//
// Here we can use some scratch memory to save ensure that at most one
// control qubit is used for costly operations such as `AddConstant`
// and `CompareGreaterThenOrEqualConstant`.
if Length(ctrls) >= 2 {
use control = Qubit();
within {
Controlled X(ctrls, control);
} apply {
Controlled ModularAddConstant([control], (modulus, c, y));
}
} else {
use carry = Qubit();
Controlled AddConstant(ctrls, (c, y + [carry]));
Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
Controlled AddConstant([carry], (modulus, y));
Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
}
}
}
/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
// We are using this version instead of the library version that is based
// on Fourier angles to show an advantage of sparse simulation in this sample.
let n = Length(y);
Fact(n > 0, "Bit width must be at least 1");
Fact(c >= 0, "constant must not be negative");
Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
if c != 0 {
// If c has j trailing zeroes than the j least significant bits
// of y won't be affected by the addition and can therefore be
// ignored by applying the addition only to the other qubits and
// shifting c accordingly.
let j = NTrailingZeroes(c);
use x = Qubit[n - j];
within {
ApplyXorInPlace(c >>> j, x);
} apply {
IncByLE(x, y[j...]);
}
}
}
/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
let bitWidth = Length(x);
if c == 0 {
X(target);
} elif c >= 2 ^ bitWidth {
// do nothing
} elif c == 2 ^ (bitWidth - 1) {
ApplyLowTCNOT(Tail(x), target);
} else {
// normalize constant
let l = NTrailingZeroes(c);
let cNormalized = c >>> l;
let xNormalized = x[l...];
let bitWidthNormalized = Length(xNormalized);
let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
use qs = Qubit[bitWidthNormalized - 1];
let cs1 = [Head(xNormalized)] + Most(qs);
let cs2 = Rest(xNormalized);
within {
for i in IndexRange(gates) {
(gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
}
} apply {
ApplyLowTCNOT(Tail(qs), target);
}
}
}
/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
within {
ApplyToEachA(X, [control1, control2]);
} apply {
ApplyAnd(control1, control2, target);
X(target);
}
}
internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
body (...) {
CCNOT(control1, control2, target);
}
adjoint (...) {
H(target);
if (M(target) == One) {
X(target);
CZ(control1, control2);
}
}
}
/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
mutable nZeroes = 0;
mutable copy = number;
while (copy % 2 == 0) {
set nZeroes += 1;
set copy /= 2;
}
return nZeroes;
}
/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
body (...) {
CNOT(a, b);
}
adjoint self;
controlled (ctls, ...) {
// In this application this operation is used in a way that
// it is controlled by at most one qubit.
Fact(Length(ctls) <= 1, "At most one control line allowed");
if IsEmpty(ctls) {
CNOT(a, b);
} else {
use q = Qubit();
within {
ApplyAnd(Head(ctls), a, q);
} apply {
CNOT(q, b);
}
}
}
controlled adjoint self;
}
Jalankan Estimator Sumber Daya
Estimator Sumber Daya menawarkan enam parameter kubit yang telah ditentukan sebelumnya, empat di antaranya memiliki set instruksi berbasis gerbang dan dua yang memiliki set instruksi Majorana. Ini juga menawarkan dua kode koreksi kesalahan kuantum, surface_code dan floquet_code.
Dalam contoh ini, Anda menjalankan Estimator Sumber Daya menggunakan qubit_gate_us_e3 parameter qubit dan surface_code kode koreksi kesalahan kuantum.
Pilih Tampilkan -> Palet Perintah, dan ketik "sumber daya" yang harus memunculkan opsi Q#: Hitung Perkiraan Sumber Daya. Anda juga dapat mengklik Perkirakan dari daftar perintah yang ditampilkan tepat sebelum
Mainoperasi. Pilih opsi ini untuk membuka jendela Estimator Sumber Daya.
Anda dapat memilih satu atau beberapa parameter Qubit + jenis kode Koreksi Kesalahan untuk memperkirakan sumber daya. Untuk contoh ini, pilih qubit_gate_us_e3 dan klik OK.

Tentukan Anggaran kesalahan atau terima nilai default 0,001. Untuk contoh ini, biarkan nilai default dan tekan Enter.
Tekan Enter untuk menerima nama hasil default berdasarkan nama file, dalam hal ini, ShorRE.
Lihat hasilnya
Estimator Sumber Daya menyediakan beberapa perkiraan untuk algoritma yang sama, masing-masing menunjukkan tradeoff antara jumlah qubit dan runtime. Memahami tradeoff antara runtime dan skala sistem adalah salah satu aspek estimasi sumber daya yang lebih penting.
Hasil estimasi sumber daya ditampilkan di jendela Perkiraan Q#.
Tab Hasil menampilkan ringkasan estimasi sumber daya. Klik ikon di samping baris pertama untuk memilih kolom yang ingin Anda tampilkan. Anda dapat memilih dari nama eksekusi, jenis perkiraan, jenis qubit, skema qec, anggaran kesalahan, qubit logis, kedalaman logis, jarak kode, status T, pabrik T, pecahan pabrik T, runtime, rQOPS, dan kubit fisik.

Di kolom Estimasi jenis tabel hasil, Anda dapat melihat jumlah kombinasi optimal {jumlah kubit, runtime} untuk algoritma Anda. Kombinasi ini dapat dilihat dalam diagram ruang-waktu.
Diagram Space-time menunjukkan tradeoff antara jumlah qubit fisik dan runtime algoritma. Dalam hal ini, Estimator Sumber Daya menemukan 13 kombinasi optimal yang berbeda dari ribuan yang mungkin. Anda dapat mengarahkan mouse ke atas setiap titik {number of qubits, runtime} untuk melihat detail estimasi sumber daya pada saat itu.
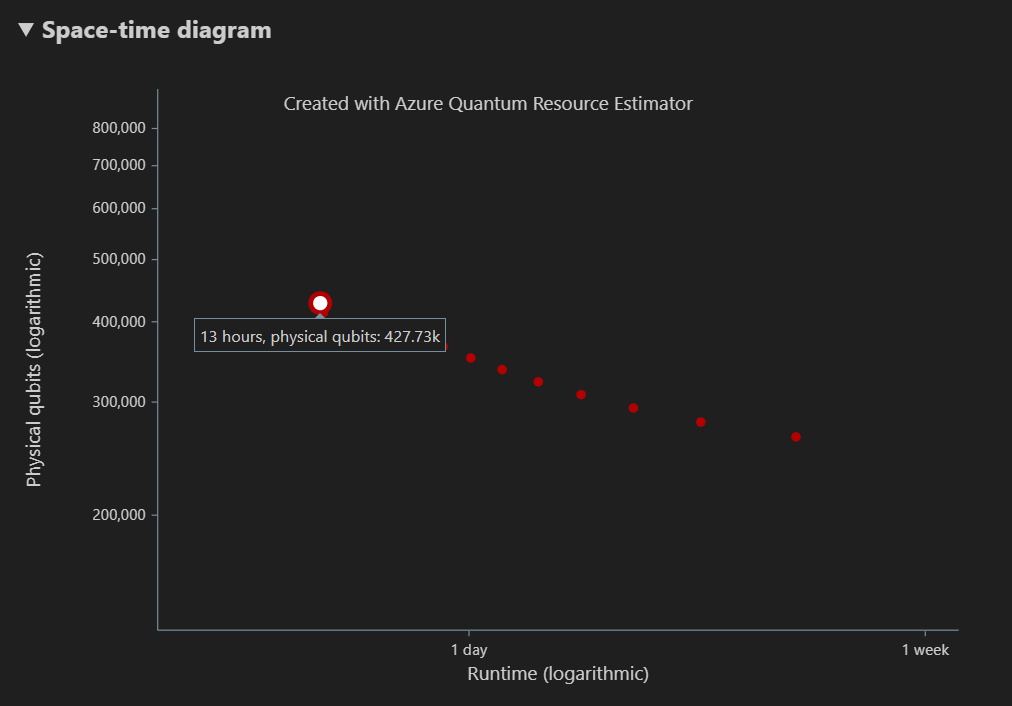
Untuk informasi selengkapnya, lihat Diagram Space-time.
Catatan
Anda perlu mengklik satu titik diagram spasi-waktu, yaitu pasangan {number of qubits, runtime}, untuk melihat diagram spasi dan detail estimasi sumber daya yang sesuai dengan titik tersebut.
Diagram Spasi menunjukkan distribusi kubit fisik yang digunakan untuk algoritma dan pabrik T, yang sesuai dengan pasangan {number of qubits, runtime}. Misalnya, jika Anda memilih titik paling kiri dalam diagram ruang-waktu, jumlah kubit fisik yang diperlukan untuk menjalankan algoritma 427726, 196686 yang merupakan kubit algoritma dan 231040 di antaranya adalah qubit pabrik T.
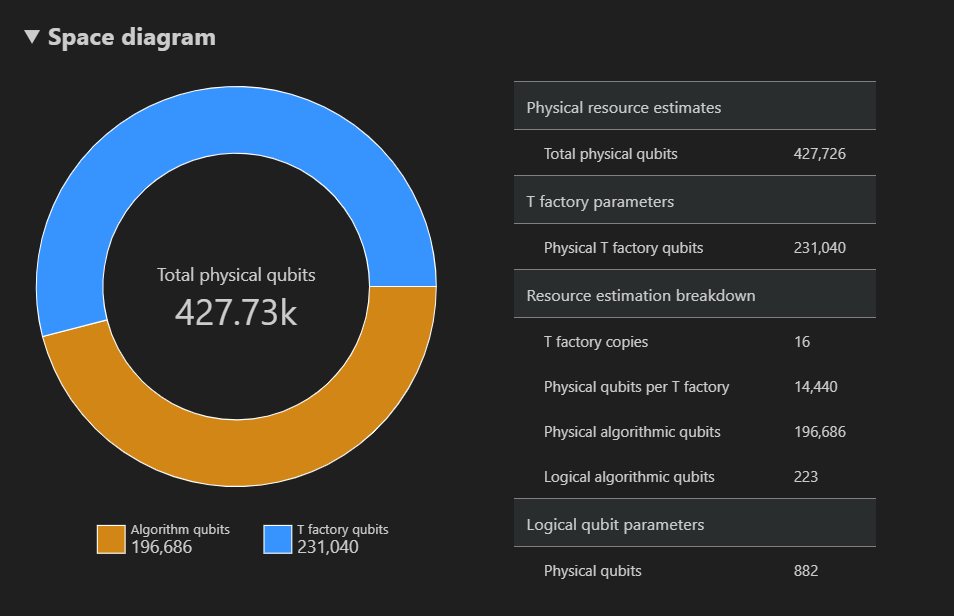
Terakhir, tab Perkiraan Sumber Daya menampilkan daftar lengkap data output untuk Estimator Sumber Daya yang sesuai dengan pasangan {number of qubits, runtime} . Anda dapat memeriksa detail biaya dengan menciutkan grup, yang memiliki informasi lebih lanjut. Misalnya, pilih titik paling kiri dalam diagram spasi-waktu dan ciutkan grup parameter kubit logis.
Parameter kubit logis Nilai Skema QEC surface_code Jarak kode 21 Qubit fisik 882 Waktu siklus logis 13 milidetik Tingkat kesalahan kubit logis 3.00E-13 Prefaktor persimpangan 0,03 Ambang koreksi kesalahan 0.01 Rumus waktu siklus logis (4 * twoQubitGateTime+ 2 *oneQubitMeasurementTime) *codeDistanceRumus qubit fisik 2 * codeDistance*codeDistanceTip
Klik Perlihatkan baris terperinci untuk menampilkan deskripsi setiap output data laporan.
Untuk informasi selengkapnya, lihat data laporan lengkap Estimator Sumber Daya.
target Mengubah parameter
Anda dapat memperkirakan biaya untuk program Q# yang sama menggunakan jenis kubit lainnya, kode koreksi kesalahan, dan anggaran kesalahan. Buka jendela Estimator Sumber Daya dengan memilih Tampilkan -> Palet Perintah, dan ketik Q#: Calculate Resource Estimates.
Pilih konfigurasi lain, misalnya parameter qubit berbasis Majorana, qubit_maj_ns_e6. Terima nilai anggaran kesalahan default atau masukkan yang baru, dan tekan Enter. Estimator Sumber Daya menjalankan kembali estimasi dengan parameter baru target .
Untuk informasi selengkapnya, lihat Target parameter untuk Estimator Sumber Daya.
Menjalankan beberapa konfigurasi parameter
Azure Quantum Resource Estimator dapat menjalankan beberapa konfigurasi target parameter dan membandingkan hasil estimasi sumber daya.
Pilih Tampilkan -> Palet Perintah, atau tekan Ctrl+Shift+P, dan ketik
Q#: Calculate Resource Estimates.Pilih qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code, dan qubit_maj_ns_e6 + floquet_code, dan klik OK.
Terima nilai anggaran kesalahan default 0,001 dan tekan Enter.
Tekan Enter untuk menerima file input, dalam hal ini, ShorRE.qs.
Dalam kasus beberapa konfigurasi parameter, hasilnya ditampilkan di baris yang berbeda di tab Hasil .
Diagram Space-time menunjukkan hasil untuk semua konfigurasi parameter. Kolom pertama tabel hasil menampilkan legenda untuk setiap konfigurasi parameter. Anda dapat mengarahkan mouse ke setiap titik untuk melihat detail estimasi sumber daya pada saat itu.
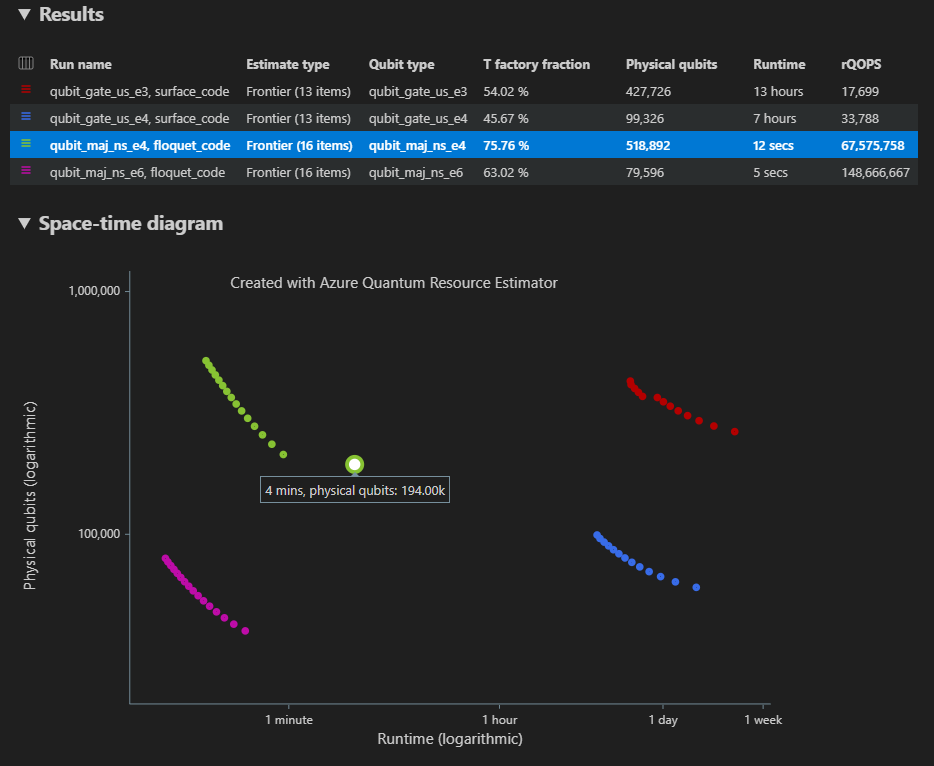
Klik {jumlah qubit, runtime} titik diagram ruang-waktu untuk memunculkan diagram ruang yang sesuai dan melaporkan data.
Prasyarat untuk Jupyter Notebook di Visual Studio Code
Lingkungan Python dengan Python dan Pip terinstal.
Versi terbaru Visual Studio Code atau buka VISUAL Code di Web.
Visual Studio Code dengan ekstensi Azure Quantum Development Kit, Python, dan Jupyter terinstal.
Azure Quantum
qsharpdanqsharp-widgetspaket terbaru.python -m pip install --upgrade qsharp qsharp-widgets
Tip
Anda tidak perlu memiliki akun Azure untuk menjalankan Estimator Sumber Daya lokal.
Membuat algoritma kuantum
Di Visual Studio Code, pilih Tampilkan Palet Perintah dan pilih Buat: Notebook Jupyter > Baru.
Di kanan atas, VISUAL Code akan mendeteksi dan menampilkan versi Python dan lingkungan Python virtual yang dipilih untuk notebook. Jika Anda memiliki beberapa lingkungan Python, Anda mungkin perlu memilih kernel menggunakan pemilih kernel di kanan atas. Jika tidak ada lingkungan yang terdeteksi, lihat Jupyter Notebooks di VISUAL Code untuk informasi penyiapan.
Di sel pertama buku catatan, impor
qsharppaket.import qsharpTambahkan sel baru dan salin kode berikut.
%%qsharp import Std.Arrays.*; import Std.Canon.*; import Std.Convert.*; import Std.Diagnostics.*; import Std.Math.*; import Std.Measurement.*; import Microsoft.Quantum.Unstable.Arithmetic.*; import Std.ResourceEstimation.*; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracle eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as little endian encoded which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { set nZeroes += 1; set copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Memperkirakan algoritma kuantum
Sekarang, Anda memperkirakan sumber daya fisik untuk RunProgram operasi menggunakan asumsi default. Tambahkan sel baru dan salin kode berikut.
result = qsharp.estimate("RunProgram()")
result
Fungsi ini qsharp.estimate membuat objek hasil, yang dapat digunakan untuk menampilkan tabel dengan jumlah sumber daya fisik keseluruhan. Anda dapat memeriksa detail biaya dengan menciutkan grup, yang memiliki informasi lebih lanjut. Untuk informasi selengkapnya, lihat data laporan lengkap Estimator Sumber Daya.
Misalnya, ciutkan grup parameter kubit Logis untuk melihat bahwa jarak kode adalah 21 dan jumlah kubit fisik adalah 882.
| Parameter kubit logis | Nilai |
|---|---|
| Skema QEC | surface_code |
| Jarak kode | 21 |
| Qubit fisik | 882 |
| Waktu siklus logis | 8 milidetik |
| Tingkat kesalahan kubit logis | 3.00E-13 |
| Prefaktor persimpangan | 0,03 |
| Ambang koreksi kesalahan | 0.01 |
| Rumus waktu siklus logis | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Rumus qubit fisik | 2 * codeDistance * codeDistance |
Tip
Untuk versi tabel output yang lebih ringkas, Anda dapat menggunakan result.summary.
Diagram spasi
Distribusi kubit fisik yang digunakan untuk algoritma dan pabrik T adalah faktor yang dapat memengaruhi desain algoritma Anda. Anda dapat menggunakan qsharp-widgets paket untuk memvisualisasikan distribusi ini untuk lebih memahami perkiraan persyaratan ruang untuk algoritma.
from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)
Dalam contoh ini, jumlah kubit fisik yang diperlukan untuk menjalankan algoritma 829766, 196686 yang merupakan kubit algoritma dan 633080 di antaranya adalah kubit pabrik T.

Mengubah nilai default dan memperkirakan algoritma
Saat mengirimkan permintaan perkiraan sumber daya untuk program Anda, Anda dapat menentukan beberapa parameter opsional. jobParams Gunakan bidang untuk mengakses semua target parameter yang dapat diteruskan ke eksekusi pekerjaan dan lihat nilai default mana yang diasumsikan:
result['jobParams']
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Anda dapat melihat bahwa Estimator Sumber Daya mengambil qubit_gate_ns_e3 model qubit, surface_code kode koreksi kesalahan, dan anggaran kesalahan 0,001 sebagai nilai default untuk estimasi.
Ini adalah target parameter yang dapat disesuaikan:
errorBudget- keseluruhan anggaran kesalahan yang diizinkan untuk algoritmaqecScheme- skema koreksi kesalahan kuantum (QEC)qubitParams- parameter qubit fisikconstraints- batasan pada tingkat komponendistillationUnitSpecifications- spesifikasi untuk algoritma penyulingan pabrik TestimateType- tunggal atau perlahan
Untuk informasi selengkapnya, lihat Target parameter untuk Estimator Sumber Daya.
Mengubah model qubit
Anda dapat memperkirakan biaya untuk algoritma yang sama menggunakan parameter qubit berbasis Majorana, qubitParams, "qubit_maj_ns_e6".
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
}})
EstimateDetails(result_maj)
Mengubah skema koreksi kesalahan kuantum
Anda dapat menjalankan ulang pekerjaan estimasi sumber daya untuk contoh yang sama pada parameter qubit berbasis Majorana dengan skema QEC floqued, qecScheme.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
}})
EstimateDetails(result_maj)
Mengubah anggaran kesalahan
Selanjutnya, jalankan ulang sirkuit kuantum yang sama dengan errorBudget 10%.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
},
"errorBudget": 0.1})
EstimateDetails(result_maj)
Batching dengan Estimator Sumber Daya
Azure Quantum Resource Estimator memungkinkan Anda menjalankan beberapa konfigurasi target parameter, dan membandingkan hasilnya. Ini berguna ketika Anda ingin membandingkan biaya model kubit, skema QEC, atau anggaran kesalahan yang berbeda.
Anda dapat melakukan estimasi batch dengan meneruskan daftar target parameter ke
paramsparameterqsharp.estimatefungsi. Misalnya, jalankan algoritma yang sama dengan parameter default dan parameter kubit berbasis Majorana dengan skema QEC floquet.result_batch = qsharp.estimate("RunProgram()", params= [{}, # Default parameters { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" } }]) result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])Model Kubit logis Kedalaman logis Status T Jarak kode Pabrik T Pecahan pabrik T Qubit fisik rQOPS Runtime fisik N berbasis gerbang, 10⁻³ 223 3.64M 4.70M 21 19 76.30 % 829,77k 26,55M 31 detik Majorana ns, 10⁻⁶ 223 3.64M 4.70M 5 19 63.02 % 79,60k 148.67M 5 detik Anda juga dapat membuat daftar parameter estimasi menggunakan
EstimatorParamskelas .from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"] params = EstimatorParams(num_items=6) params.error_budget = 0.333 params.items[0].qubit_params.name = QubitParams.GATE_US_E3 params.items[1].qubit_params.name = QubitParams.GATE_US_E4 params.items[2].qubit_params.name = QubitParams.GATE_NS_E3 params.items[3].qubit_params.name = QubitParams.GATE_NS_E4 params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4 params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6 params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODEqsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)Model Kubit logis Kedalaman logis Status T Jarak kode Pabrik T Pecahan pabrik T Qubit fisik rQOPS Runtime fisik Berbasis gerbang μs, 10⁻³ 223 3,64M 4.70M 17 13 40.54 % 216,77k 21,86k 10 Jam Berbasis gerbang μs, 10⁻⁴ 223 3.64M 4.70M 9 14 43.17 % 63,57k 41,30k 5 Jam N berbasis gerbang, 10⁻³ 223 3,64M 4.70M 17 16 69.08 % 416,89k 32.79M 25 detik Ns berbasis gerbang, 10⁻⁴ 223 3,64M 4.70M 9 14 43.17 % 63,57k 61,94M 13 detik Majorana ns, 10⁻⁴ 223 3,64M 4.70M 9 19 82.75 % 501,48k 82,59M 10 detik Majorana ns, 10⁻⁶ 223 3,64M 4.70M 5 13 31.47 % 42,96k 148.67M 5 detik
Menjalankan estimasi perlahan Pareto
Saat memperkirakan sumber daya algoritma, penting untuk mempertimbangkan tradeoff antara jumlah kubit fisik dan runtime algoritma. Anda dapat mempertimbangkan alokasi kubit fisik sebanyak mungkin untuk mengurangi runtime algoritma. Namun, jumlah qubit fisik dibatasi oleh jumlah kubit fisik yang tersedia di perangkat keras kuantum.
Estimasi perbatasan Pareto memberikan beberapa perkiraan untuk algoritma yang sama, masing-masing dengan tradeoff antara jumlah qubit dan runtime.
Untuk menjalankan Estimator Sumber Daya menggunakan estimasi frontier Pareto, Anda perlu menentukan
"estimateType"target parameter sebagai"frontier". Misalnya, jalankan algoritma yang sama dengan parameter kubit berbasis Majorana dengan kode permukaan menggunakan estimasi perbatasan Pareto.result = qsharp.estimate("RunProgram()", params= {"qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # frontier estimation } )Anda dapat menggunakan
EstimatesOverviewfungsi untuk menampilkan tabel dengan jumlah sumber daya fisik secara keseluruhan. Klik ikon di samping baris pertama untuk memilih kolom yang ingin Anda tampilkan. Anda dapat memilih dari nama eksekusi, jenis perkiraan, jenis qubit, skema qec, anggaran kesalahan, qubit logis, kedalaman logis, jarak kode, status T, pabrik T, pecahan pabrik T, runtime, rQOPS, dan kubit fisik.from qsharp_widgets import EstimatesOverview EstimatesOverview(result)
Di kolom Estimasi jenis tabel hasil, Anda dapat melihat jumlah kombinasi {jumlah kubit, runtime} yang berbeda untuk algoritma Anda. Dalam hal ini, Estimator Sumber Daya menemukan 22 kombinasi optimal yang berbeda dari ribuan yang mungkin.
Diagram waktu spasi
Fungsi ini EstimatesOverview juga menampilkan diagram ruang-waktu Resource Estimator.
Diagram space-time menunjukkan jumlah qubit fisik dan runtime algoritma untuk setiap pasangan {number of qubits, runtime}. Anda dapat mengarahkan mouse ke setiap titik untuk melihat detail estimasi sumber daya pada saat itu.

Batching dengan estimasi perlahan Pareto
Untuk memperkirakan dan membandingkan beberapa konfigurasi target parameter dengan estimasi frontier, tambahkan
"estimateType": "frontier",ke parameter .result = qsharp.estimate( "RunProgram()", [ { "qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # Pareto frontier estimation }, { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" }, "estimateType": "frontier", # Pareto frontier estimation }, ] ) EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])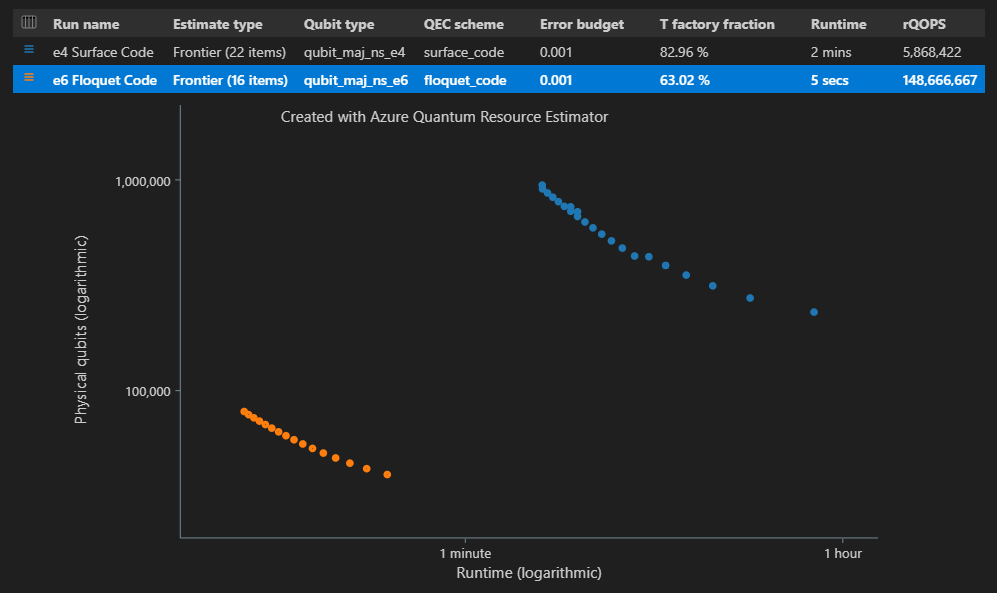
Catatan
Anda dapat menentukan warna dan menjalankan nama untuk diagram qubit-time menggunakan fungsi .
EstimatesOverviewSaat menjalankan beberapa konfigurasi target parameter menggunakan estimasi perbatasan Pareto, Anda dapat melihat perkiraan sumber daya untuk titik tertentu dari diagram ruang-waktu, yaitu untuk setiap pasangan {number of qubits, runtime}. Misalnya, kode berikut menunjukkan perkiraan penggunaan detail untuk runtime terpendek kedua (estimasi index=0) dan runtime terpendek keempat (indeks poin=3).
EstimateDetails(result[1], 4)Anda juga dapat melihat diagram spasi untuk titik tertentu dari diagram ruang-waktu. Misalnya, kode berikut menunjukkan diagram spasi untuk eksekusi kombinasi pertama (perkiraan index=0) dan runtime terpendek ketiga (indeks titik=2).
SpaceChart(result[0], 2)
Prasyarat untuk Qiskit
- Akun Azure dengan langganan aktif. Jika Anda tidak memiliki akun Azure, daftarkan secara gratis dan daftar untuk langganan prabayar.
- Ruang kerja Azure Quantum. Untuk informasi selengkapnya, lihat Buat ruang kerja Azure Quantum.
Mengaktifkan Azure Quantum Resource Estimator target di ruang kerja Anda
Estimator Sumber Daya adalah target penyedia Komputasi Microsoft Quantum. Jika Anda telah membuat ruang kerja sejak rilis Estimator Sumber Daya, penyedia Komputasi Microsoft Quantum ditambahkan ke ruang kerja Anda secara otomatis.
Jika Anda menggunakan ruang kerja Azure Quantum yang sudah ada :
- Buka ruang kerja Anda di portal Azure.
- Di panel kiri, di bawah Operasi, pilih Penyedia.
- Pilih + Tambahkan penyedia.
- Pilih + Tambahkan untuk Microsoft Quantum Computing.
- Pilih Pelajari & Kembangkan dan pilih Tambahkan.
Membuat buku catatan baru di ruang kerja Anda
- Masuk ke portal Microsoft Azure dan pilih ruang kerja Azure Quantum Anda.
- Di bawah Operasi, pilih Buku Catatan
- Klik Buku Catatan Saya dan klik Tambahkan Baru
- Di Jenis Kernel, pilih IPython.
- Ketik nama untuk file tersebut, dan klik Buat file.
Saat buku catatan baru Anda terbuka, buku catatan akan secara otomatis membuat kode untuk sel pertama, berdasarkan informasi langganan dan ruang kerja Anda.
from azure.quantum import Workspace
workspace = Workspace (
resource_id = "", # Your resource_id
location = "" # Your workspace location (for example, "westus")
)
Catatan
Kecuali dinyatakan lain, Anda harus menjalankan setiap sel saat Anda membuatnya untuk menghindari masalah kompilasi.
Klik ikon segitiga "putar" di sebelah kiri sel untuk menjalankan kode.
Memuat impor yang diperlukan
Pertama, Anda harus mengimpor modul tambahan dari azure-quantum dan qiskit.
Klik + Kode untuk menambahkan sel baru, lalu tambahkan dan jalankan kode berikut:
from azure.quantum.qiskit import AzureQuantumProvider
from qiskit import QuantumCircuit, transpile
from qiskit.circuit.library import RGQFTMultiplier
Menyambungkan ke layanan Azure Quantum
Selanjutnya, buat objek AzureQuantumProvider menggunakan workspace objek dari sel sebelumnya untuk menyambungkan ke ruang kerja Azure Quantum Anda. Anda membuat instans backend dan mengatur Estimator Sumber Daya sebagai target.
provider = AzureQuantumProvider(workspace)
backend = provider.get_backend('microsoft.estimator')
Membuat algoritma kuantum
Dalam contoh ini, Anda membuat sirkuit kuantum untuk pengali berdasarkan konstruksi yang disajikan dalam Ruiz-Perez dan Garcia-Escartin (arXiv:1411.5949) yang menggunakan Quantum Fourier Transform untuk mengimplementasikan aritmatika.
Anda dapat menyesuaikan ukuran pengali dengan mengubah bitwidth variabel. Pembuatan sirkuit dibungkus dalam fungsi yang dapat dipanggil dengan bitwidth nilai pengali. Operasi akan memiliki dua register input, masing-masing ukuran , dan satu register output yang ditentukan bitwidthyang dua kali ukuran yang ditentukan bitwidth. Fungsi ini juga akan mencetak beberapa jumlah sumber daya logis untuk pengali yang diekstrak langsung dari sirkuit kuantum.
def create_algorithm(bitwidth):
print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
# Print a warning for large bitwidths that will require some time to generate and
# transpile the circuit.
if bitwidth > 18:
print(f"[WARN] It will take more than one minute generate a quantum circuit with a bitwidth larger than 18")
circ = RGQFTMultiplier(num_state_qubits=bitwidth, num_result_qubits=2 * bitwidth)
# One could further reduce the resource estimates by increasing the optimization_level,
# however, this will also increase the runtime to construct the algorithm. Note, that
# it does not affect the runtime for resource estimation.
print(f"[INFO] Decompose circuit into intrinsic quantum operations")
circ = transpile(circ, basis_gates=SUPPORTED_INSTRUCTIONS, optimization_level=0)
# print some statistics
print(f"[INFO] qubit count: {circ.num_qubits}")
print("[INFO] gate counts")
for gate, count in circ.count_ops().items():
print(f"[INFO] - {gate}: {count}")
return circ
Catatan
Anda dapat mengirimkan pekerjaan estimasi sumber daya fisik untuk algoritma yang tidak memiliki status T, tetapi yang memiliki setidaknya satu pengukuran.
Memperkirakan algoritma kuantum
Buat instans algoritma Anda menggunakan create_algorithm fungsi . Anda dapat menyesuaikan ukuran pengali dengan mengubah bitwidth variabel.
bitwidth = 4
circ = create_algorithm(bitwidth)
Perkirakan sumber daya fisik untuk operasi ini menggunakan asumsi default. Anda dapat mengirimkan sirkuit ke backend Estimator Sumber Daya menggunakan run metode , lalu menjalankan job.result() untuk menunggu pekerjaan selesai dan mengembalikan hasilnya.
job = backend.run(circ)
result = job.result()
result
Ini membuat tabel yang memperlihatkan jumlah sumber daya fisik secara keseluruhan. Anda dapat memeriksa detail biaya dengan menciutkan grup, yang memiliki informasi lebih lanjut.
Tip
Untuk versi tabel output yang lebih ringkas, Anda dapat menggunakan result.summary.
Misalnya, jika Anda menciutkan grup parameter Kubit logis, Anda dapat lebih mudah melihat bahwa jarak kode koreksi kesalahan adalah 15.
| Parameter kubit logis | Nilai |
|---|---|
| Skema QEC | surface_code |
| Jarak kode | 15 |
| Qubit fisik | 450 |
| Waktu siklus logis | 6us |
| Tingkat kesalahan kubit logis | 3.00E-10 |
| Prefaktor persimpangan | 0,03 |
| Ambang koreksi kesalahan | 0.01 |
| Rumus waktu siklus logis | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Rumus qubit fisik | 2 * codeDistance * codeDistance |
Dalam grup Parameter kubit fisik, Anda dapat melihat properti kubit fisik yang diasumsikan untuk estimasi ini. Misalnya, waktu untuk melakukan pengukuran kubit tunggal dan gerbang qubit tunggal diasumsikan masing-masing 100 ns dan 50 ns.
Tip
Anda juga dapat mengakses output Estimator Sumber Daya sebagai kamus Python menggunakan metode result.data().
Untuk informasi selengkapnya, lihat daftar lengkap data output untuk Estimator Sumber Daya.
Diagram spasi
Distribusi kubit fisik yang digunakan untuk algoritma dan pabrik T adalah faktor yang dapat memengaruhi desain algoritma Anda. Anda dapat memvisualisasikan distribusi ini untuk lebih memahami perkiraan persyaratan ruang untuk algoritma.
result.diagram.space

Diagram ruang menunjukkan proporsi algoritma qubit dan T factory qubits. Perhatikan bahwa jumlah salinan pabrik T, 28, berkontribusi pada jumlah kubit fisik untuk pabrik T sebagai $\text{T factories} \cdot \text{kubit fisik per pabrik T}= 28 \cdot 18.000 = 504.000$.
Untuk informasi selengkapnya, lihat Estimasi fisik pabrik T.
Mengubah nilai default dan memperkirakan algoritma
Saat mengirimkan permintaan perkiraan sumber daya untuk program Anda, Anda dapat menentukan beberapa parameter opsional. jobParams Gunakan bidang untuk mengakses semua nilai yang dapat diteruskan ke eksekusi pekerjaan dan lihat nilai default mana yang diasumsikan:
result.data()["jobParams"]
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Ini adalah target parameter yang dapat disesuaikan:
errorBudget- anggaran kesalahan yang diizinkan secara keseluruhanqecScheme- skema koreksi kesalahan kuantum (QEC)qubitParams- parameter qubit fisikconstraints- batasan pada tingkat komponendistillationUnitSpecifications- spesifikasi untuk algoritma penyulingan pabrik T
Untuk informasi selengkapnya, lihat Target parameter untuk Estimator Sumber Daya.
Mengubah model qubit
Selanjutnya, perkirakan biaya untuk algoritma yang sama menggunakan parameter qubit berbasis Majorana qubit_maj_ns_e6
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
})
result = job.result()
result
Anda dapat memeriksa jumlah fisik secara terprogram. Misalnya, Anda dapat menjelajahi detail tentang pabrik T yang dibuat untuk menjalankan algoritma.
result.data()["tfactory"]
{'eccDistancePerRound': [1, 1, 5],
'logicalErrorRate': 1.6833177305222897e-10,
'moduleNamePerRound': ['15-to-1 space efficient physical',
'15-to-1 RM prep physical',
'15-to-1 RM prep logical'],
'numInputTstates': 20520,
'numModulesPerRound': [1368, 20, 1],
'numRounds': 3,
'numTstates': 1,
'physicalQubits': 16416,
'physicalQubitsPerRound': [12, 31, 1550],
'runtime': 116900.0,
'runtimePerRound': [4500.0, 2400.0, 110000.0]}
Catatan
Secara default, runtime ditampilkan dalam nanodetik.
Anda dapat menggunakan data ini untuk menghasilkan beberapa penjelasan tentang bagaimana pabrik T menghasilkan status T yang diperlukan.
data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]
print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
print(f"""- {tfactory["numModulesPerRound"][round]} {tfactory["moduleNamePerRound"][round]} unit(s)""")
A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)
Mengubah skema koreksi kesalahan kuantum
Sekarang, jalankan kembali pekerjaan estimasi sumber daya untuk contoh yang sama pada parameter qubit berbasis Majorana dengan skema QEC floqued, qecScheme.
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
},
qecScheme={
"name": "floquet_code"
})
result_maj_floquet = job.result()
result_maj_floquet
Mengubah anggaran kesalahan
Mari kita jalankan kembali sirkuit kuantum yang sama dengan errorBudget 10%.
job = backend.run(circ,
qubitParams={
"name": "qubit_maj_ns_e6"
},
qecScheme={
"name": "floquet_code"
},
errorBudget=0.1)
result_maj_floquet_e1 = job.result()
result_maj_floquet_e1
Catatan
Jika Anda mengalami masalah saat bekerja dengan Estimator Sumber Daya, lihat halaman Pemecahan Masalah, atau hubungi AzureQuantumInfo@microsoft.com.