Metrik kode - Kompleksitas Siklomatik

Saat bekerja dengan metrik kode, salah satu item yang paling tidak dipahami tampaknya merupakan kompleksitas cyclomatic. Pada dasarnya, dengan kompleksitas siklomatik, angka yang lebih tinggi buruk dan angka yang lebih rendah baik. Anda dapat menggunakan kompleksitas siklomatik untuk mengetahui seberapa sulit kode yang diberikan untuk menguji, memelihara, atau memecahkan masalah, dan mengetahui seberapa besar kemungkinan kode tersebut akan menghasilkan kesalahan. Pada tingkat tinggi, kami menentukan nilai kompleksitas siklomatik dengan menghitung jumlah keputusan yang dibuat dalam kode sumber Anda. Dalam artikel ini, Anda memulai dengan contoh sederhana kompleksitas siklomatik untuk memahami konsep dengan cepat, lalu melihat beberapa informasi tambahan tentang penggunaan aktual dan batas yang disarankan. Terakhir, ada bagian kutipan yang dapat digunakan untuk menggali lebih dalam subjek ini.

Contoh

Kompleksitas siklomatik didefinisikan sebagai ukuran "jumlah logika keputusan dalam fungsi kode sumber" NIST235. Sederhananya, semakin banyak keputusan yang harus dibuat dalam kode, semakin kompleks.

Mari kita lihat bagaimana caranya berfungsi. Buat aplikasi konsol baru dan segera hitung metrik kode Anda dengan masuk ke Analisis > Hitung Metrik Kode untuk Solusi.

Perhatikan bahwa kompleksitas siklomatik berada pada nilai 2 (nilai terendah yang mungkin). Jika Anda menambahkan kode non-keputusan, perhatikan kompleksitas tidak berubah:

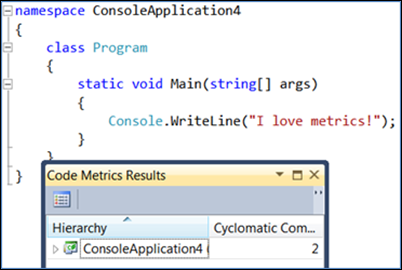
Jika Anda menambahkan keputusan, nilai kompleksitas siklomatik naik satu per satu:

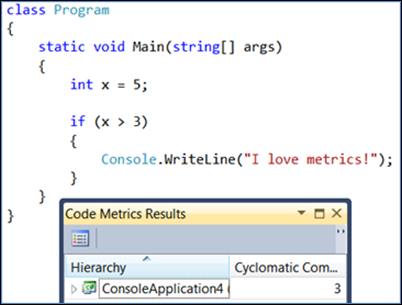
Ketika Anda mengubah pernyataan if menjadi pernyataan pengalihan dengan empat keputusan yang akan dibuat kemudian, itu berubah dari dua asli menjadi enam:

Mari kita lihat basis kode yang lebih besar (hipotetis).

Perhatikan bahwa sebagian besar item, saat Anda menelusuri paling detail ke kelas Products_Related, memiliki nilai satu tetapi beberapa dari mereka memiliki kompleksitas lima. Dengan sendirinya, perbedaan ini mungkin bukan masalah besar, tetapi mengingat bahwa sebagian besar anggota lain memiliki satu di kelas yang sama, Anda pasti harus melihat lebih dekat pada dua item tersebut dan melihat apa yang ada di dalamnya. Anda dapat melihat lebih dekat dengan mengklik kanan item dan memilih Buka Kode Sumber dari menu konteks. Lihat lebih dekat Product.set(Product):

Mengingat semua pernyataan kondisional, Anda dapat melihat mengapa kompleksitas siklomatik bernilai lima. Pada titik ini, Anda dapat memutuskan bahwa hasil ini adalah tingkat kompleksitas yang dapat diterima, atau Anda mungkin melakukan refaktor untuk mengurangi kompleksitas.

Angka Ajaib

Seperti banyak metrik dalam industri ini, tidak ada batas kompleksitas siklomatik yang tepat yang sesuai dengan semua organisasi. Namun, NIST235 memang menunjukkan bahwa batas 10 adalah titik awal yang baik:

"Angka yang tepat untuk digunakan sebagai batas, bagaimanapun, tetap agak kontroversial. Batas asli 10 seperti yang diusulkan oleh McCabe memiliki bukti pendukung yang signifikan, tetapi batas setingkat 15 telah berhasil digunakan juga. Batas lebih dari 10 harus dicadangkan untuk proyek yang memiliki beberapa keuntungan operasional daripada proyek umum, misalnya staf berpengalaman, desain formal, bahasa pemrograman modern, pemrograman terstruktur, panduan kode, dan rencana pengujian yang komprehensif. Dengan kata lain, organisasi dapat memilih batas kompleksitas yang lebih besar dari 10, tetapi hanya jika yakin tahu apa yang dilakukannya dan bersedia untuk mencuatkan upaya pengujian tambahan yang diperlukan oleh modul yang lebih kompleks." NIST235

Kompleksitas Cyclomatic dan Nomor Garis

Hanya melihat jumlah baris kode tanpa konteks lain adalah, paling tidak, sebuah prediktor kualitas kode yang sangat umum. Ada beberapa kebenaran dasar untuk gagasan bahwa semakin banyak baris kode dalam fungsi, semakin besar kemungkinan memiliki kesalahan. Namun, ketika Anda menggabungkan kompleksitas siklomatik dengan baris kode, maka Anda memiliki gambaran yang jauh lebih jelas tentang potensi kesalahan.

Seperti yang dijelaskan oleh Pusat Teknologi Jaminan Perangkat Lunak (SATC) di NASA:

SATC telah menemukan bahwa evaluasi yang paling efektif adalah kombinasi dari ukuran dan kompleksitas Siklomatik. Modul dengan kompleksitas tinggi dan ukuran besar cenderung memiliki keandalan terendah. Modul dengan ukuran rendah dan kompleksitas tinggi juga merupakan risiko keandalan karena cenderung kode sangat terse, yang sulit diubah atau dimodifikasi." SATC

Analisis Kode

Analisis kode mencakup kategori aturan Keberlanjutan. Untuk informasi selengkapnya, lihat aturan pemeliharaan . Saat menggunakan analisis kode warisan, seperangkat aturan Extended Design Guideline berisi area pemeliharaan:

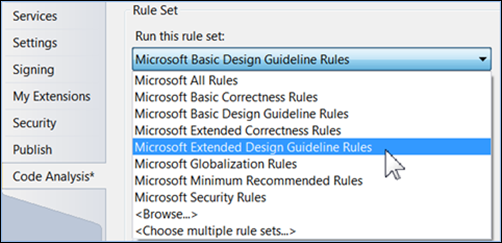
Di area pemeliharaan terdapat aturan tentang kompleksitas.

Aturan ini mengeluarkan peringatan ketika kompleksitas siklomatik mencapai 25, sehingga dapat membantu Anda menghindari kompleksitas yang berlebihan. Untuk mempelajari selengkapnya tentang aturan, lihat CA1502

Menyatukan Semuanya

Intinya adalah bahwa angka kompleksitas tinggi berarti kemungkinan kesalahan yang lebih besar dengan peningkatan waktu untuk mempertahankan dan memecahkan masalah. Lihat lebih dekat fungsi apa pun yang memiliki kompleksitas tinggi dan putuskan apakah fungsi tersebut harus direfaktor untuk membuatnya kurang kompleks.

Kutipan

MCCABE5

McCabe, T. dan A. Watson (1994), Kompleksitas Perangkat Lunak (CrossTalk: Jurnal Rekayasa Perangkat Lunak Pertahanan).

NIST235

Watson, A. H., & McCabe, T. J. (1996). Pengujian Terstruktur: Metodologi Pengujian Menggunakan Metrik Kompleksitas Siklomatik (Publikasi Khusus NIST 500-235). Diakses tanggal 14 Mei 2011, dari situs web McCabe Software: http://www.mccabe.com/pdf/mccabe-nist235r.pdf

SATC

Rosenberg, L., Hammer, T., Shaw, J. (1998). Metrik dan Keandalan Perangkat Lunak (Proses Simposium Internasional IEEE tentang Rekayasa Keandalan Perangkat Lunak). Diakses tanggal 14 Mei 2011, dari situs web Penn State University: https://citeseerx.ist.psu.edu/pdf/31e3f5732a7af3aecd364b6cc2a85d9495b5c159