Bagikan melalui

Persamaan PRT (Direct3D 9)

Untuk sepenuhnya memahami shader yang mengimplementasikan PRT, berguna untuk memperoleh rumus yang digunakan shader untuk menghitung radiasi keluar.

Untuk memulai, persamaan berikut adalah persamaan umum untuk menghitung radiasi keluar yang dihasilkan dari pencahayaan langsung pada objek difus dengan pencahayaan jauh yang semena-mena.

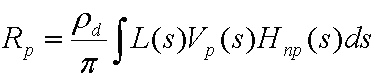
persamaan radiasi keluar yang dihasilkan dari pencahayaan langsung pada objek difus dengan pencahayaan jauh semena-mena

mana:

Parameter Deskripsi
Rp Radiasi keluar di vertex p. Dievaluasi di setiap puncak pada jala.
pd Albedo permukaan.
Pi Konstanta, digunakan sebagai faktor normalisasi konservasi energi.
L Lingkungan pencahayaan (radiasi sumber).
Vp₍s₎ Fungsi visibilitas biner untuk titik p. Ini adalah 1 jika titik dapat melihat cahaya, 0 jika tidak.
Hnp₍s₎ Istilah kosinus dari hukum Lambert. Sama dengan maks((Np· s), 0) di mana Np adalah permukaan normal pada titik p.
s Variabel yang terintegrasi di atas bola.

 

Menggunakan fungsi dasar bulat, seperti harmonik bulat, persamaan berikut mempertanyakan lingkungan pencahayaan.

persamaan lingkungan pencahayaan

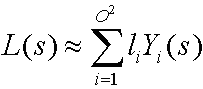
mana:

Parameter Deskripsi
L Lingkungan pencahayaan (radiasi sumber).
saya Bilangan bulat yang menjumlahkan jumlah fungsi dasar.
O Urutan harmonik bola.
Aku Koefisien.
Y i Beberapa fungsi dasar di atas bola.

 

Pengumpulan koefisien ini, L', memberikan perkiraan optimal untuk L fungsi dengan fungsi dasar Y. Mengganti dan mendistribusikan menghasilkan persamaan berikut.

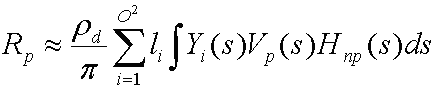
persamaan radiasi keluar setelah mengganti l dan mendistribusikan

Integral dari YiVp₍s₎Hnp₍s₎ adalah koefisien transfer tpi yang diawali simulator untuk setiap puncak pada jala. Mengganti ini menghasilkan persamaan berikut.

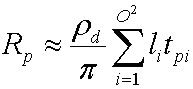
persamaan radiasi keluar setelah mengganti koefisien transfer

Mengubah ini ke notasi vektor menghasilkan persamaan yang tidak dikompresi berikut untuk menghitung radiasi keluar untuk setiap saluran.

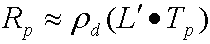
persamaan radiasi keluar setelah berubah menjadi notasi vektor

mana:

Parameter Deskripsi
Rp Radiasi keluar di vertex p.
pd Albedo permukaan.
L' Vektor li, dan merupakan proyeksi dari pancaran sumber ke dalam fungsi dasar harmonis bubuk. Ini adalah vektor order² koefisien harmonik bulat.
Tp Vektor transfer order² untuk vertex p. Simulator membagi koefisien transfer dengan p.

 

Kedua vektor ini adalah vektor koefisien harmonis bulat order², jadi perhatikan bahwa ini hanyalah produk titik. Tergantung pada pesanan, titik bisa mahal sehingga kompresi dapat digunakan. Algoritma yang disebut Clustered Principal Component Analysis (CPCA) secara efisien mengompresi data. Ini memungkinkan penggunaan perkiraan harmonik sferis dengan urutan yang lebih tinggi yang menghasilkan bayangan yang lebih tajam.

CPCA menyediakan persamaan berikut untuk memperkirakan vektor transfer.

persamaan perkiraan vektor transfer

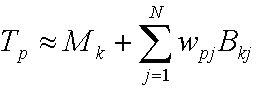
mana:

Parameter Deskripsi
Tp Vektor transfer untuk vertex p.
Mk Rata-rata untuk k kluster.
j Bilangan bulat yang menjumlahkan jumlah vektor PCA.
N Jumlah vektor PCA.
wpj Bobot PCA jth untuk titik p.
Bkj Vektor dasar PCA jth untuk k kluster.

 

Kluster hanyalah beberapa simpul yang memiliki vektor rata-rata yang sama. Cara mendapatkan rata-rata kluster, bobot PCA, vektor dasar PCA, dan id kluster untuk simpul dibahas di bawah ini.

Mengganti kedua persamaan ini menghasilkan:

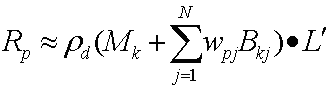
persamaan radiasi keluar setelah mengganti vektor transfer

Kemudian mendistribusikan produk titik menghasilkan persamaan berikut.

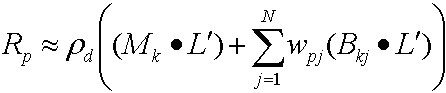
persamaan radiasi keluar setelah mendistribusikan produk titik

Karena keduanya (Mk· L') dan (Bkj· L') adalah konstanta per puncak, sampel menghitung nilai-nilai ini dengan CPU dan meneruskannya sebagai konstanta ke dalam shader vertex; karena wpj perubahan untuk setiap puncak, sampel menyimpan data per vertex ini di buffer vertex.

Transfer Radiance Yang Telah Dikomputasi