Representasi Matriks Transformasi

Matriks m×n adalah sekumpulan angka yang disusun dalam baris m dan kolom n. Ilustrasi berikut menunjukkan beberapa matriks.

ilustrasi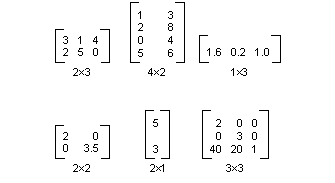

Anda dapat menambahkan dua matriks dengan ukuran yang sama dengan menambahkan elemen individual. Ilustrasi berikut menunjukkan dua contoh penambahan matriks.

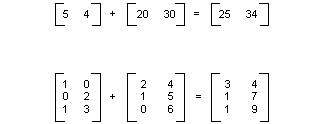
Matriks m×n dapat dikalikan dengan matriks n×p, dan hasilnya adalah matriks m×p. Jumlah kolom dalam matriks pertama harus sama dengan jumlah baris dalam matriks kedua. Misalnya, matriks 4 ×2 dapat dikalikan dengan matriks 2 ×3 untuk menghasilkan matriks 4 ×3.

Poin dalam bidang dan baris dan kolom matriks dapat dianggap sebagai vektor. Misalnya, (2, 5) adalah vektor dengan dua komponen, dan (3, 7, 1) adalah vektor dengan tiga komponen. Produk titik dari dua vektor didefinisikan sebagai berikut:

(a, b) • (c, d) = ac + bd

(a, b, c) • (d, e, f) = ad + be + cf

Misalnya, produk titik (2, 3) dan (5, 4) adalah (2)(5) + (3)(4) = 22. Produk titik (2, 5, 1) dan (4, 3, 1) adalah (2)(4) + (5)(3) + (1)(1) = 24. Perhatikan bahwa produk titik dari dua vektor adalah angka, bukan vektor lain. Perhatikan juga bahwa Anda dapat menghitung produk titik hanya jika kedua vektor memiliki jumlah komponen yang sama.

Biarkan A(i, j) menjadi entri dalam matriks A di baris ith dan kolom jth. Misalnya A(3, 2) adalah entri dalam matriks A di baris3 rd dan kolom 2nd. Misalkan A, B, dan C adalah matriks, dan AB = C. Entri C dihitung sebagai berikut:

C(i, j) = (baris i dari A) • (kolom j dari B)

Ilustrasi berikut menunjukkan beberapa contoh perkalian matriks.

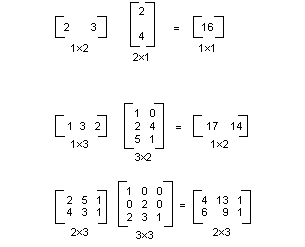
Jika Anda menganggap titik dalam bidang sebagai matriks 1 × 2, Anda dapat mengubah titik tersebut dengan mengalikannya dengan matriks 2 × 2. Ilustrasi berikut menunjukkan beberapa transformasi yang diterapkan ke titik (2, 1).

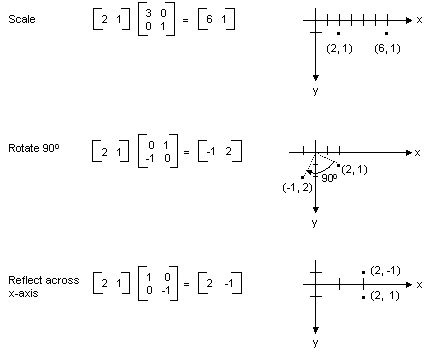
Semua transformasi yang ditunjukkan pada gambar sebelumnya adalah transformasi linier. Transformasi tertentu lainnya, seperti terjemahan, tidak linier, dan tidak dapat diekspresikan sebagai perkalian dengan matriks 2 × 2. Misalkan Anda ingin memulai dengan titik (2, 1), putar 90 derajat, terjemahkan 3 unit ke arah x, dan terjemahkan 4 unit ke arah y. Anda dapat menyelesaikan ini dengan melakukan perkalian matriks diikuti dengan penambahan matriks.

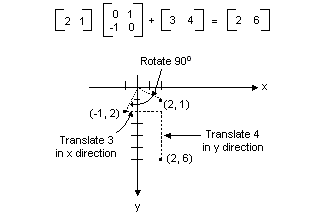
Transformasi linier (perkalian dengan matriks 2 × 2) diikuti dengan terjemahan (penambahan matriks 1 × 2) disebut transformasi affine. Alternatif untuk menyimpan transformasi affine dalam sepasang matriks (satu untuk bagian linier dan satu untuk terjemahan) adalah menyimpan seluruh transformasi dalam 3 × 3 matriks. Untuk membuat pekerjaan ini, titik dalam bidang harus disimpan dalam matriks 1 × 3 dengan koordinat ke-3 dummy. Teknik yang biasa adalah membuat semua koordinat ke-3 sama dengan 1. Misalnya, titik (2, 1) diwakili oleh matriks [2 1 1]. Ilustrasi berikut menunjukkan transformasi affine (putar 90 derajat; terjemahkan 3 unit ke arah x, 4 unit dalam arah y) dinyatakan sebagai perkalian dengan 3 × 3 matriks tunggal.

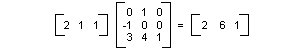
Dalam contoh sebelumnya, titik (2, 1) dipetakan ke titik (2, 6). Perhatikan bahwa kolom ketiga 3 × 3 matriks berisi angka 0, 0, 1. Ini akan selalu terjadi untuk 3 × 3 matriks transformasi affine. Angka penting adalah enam angka dalam kolom 1 dan 2. Bagian kiri atas 2 × 2 matriks mewakili bagian linier transformasi, dan dua entri pertama dalam baris ke-3 mewakili terjemahan.

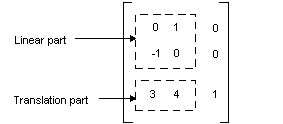
Di Windows GDI+ Anda dapat menyimpan transformasi affine dalam objek Matrix. Karena kolom ketiga matriks yang mewakili transformasi affine selalu (0, 0, 1), Anda hanya menentukan enam angka dalam dua kolom pertama saat Anda membuat objek Matriks. Pernyataan Matrix myMatrix(0.0f, 1.0f, -1.0f, 0.0f, 3.0f, 4.0f); membangun matriks yang ditunjukkan pada gambar sebelumnya.

Transformasi Komposit

Transformasi komposit adalah urutan transformasi, satu diikuti oleh yang lain. Pertimbangkan matriks dan transformasi dalam daftar berikut:

• Matriks A Putar 90 derajat
• Skala Matriks B dengan faktor 2 ke arah x
• Matriks C Terjemahkan 3 unit ke arah y

Jika Anda mulai dengan titik (2, 1) — diwakili oleh matriks [2 1 1] — dan dikalikan dengan A, maka B, maka C, titik (2,1) akan menjalani tiga transformasi dalam urutan yang tercantum.

[2 1 1]ABC = [ –2 5 1]

Daripada menyimpan tiga bagian transformasi komposit dalam tiga matriks terpisah, Anda dapat mengalikan A, B, dan C bersama-sama untuk mendapatkan satu 3 × 3 matriks yang menyimpan seluruh transformasi komposit. Misalkan ABC = D. Kemudian titik yang dikalikan dengan D memberikan hasil yang sama dengan titik yang dikalikan dengan A, lalu B, lalu C.

[2 1 1]D = [ –2 5 1]

Ilustrasi berikut menunjukkan matriks A, B, C, dan D.

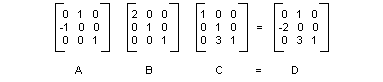
Fakta bahwa matriks transformasi komposit dapat dibentuk dengan mengalikan matriks transformasi individu berarti bahwa urutan transformasi affine dapat disimpan dalam satu objek Matrix.

Nota

Urutan transformasi komposit penting. Secara umum, putar, lalu skalakan, lalu terjemahkan tidak sama dengan skala, lalu putar, lalu terjemahkan. Demikian pula, urutan perkalian matriks penting. Secara umum, ABC tidak sama dengan BAC.

 

Kelas Matrix menyediakan beberapa metode untuk membangun transformasi komposit: Matrix::Multiply, Matrix::Rotate, Matriks::RotateAt, Matrix::Scale, Matrix::Shear, dan Matrix::Menerjemahkan. Contoh berikut membuat matriks transformasi komposit yang pertama kali memutar 30 derajat, lalu menskalakan dengan faktor 2 ke arah y, lalu menerjemahkan 5 unit ke arah x.

Matrix myMatrix;
myMatrix.Rotate(30.0f);
myMatrix.Scale(1.0f, 2.0f, MatrixOrderAppend);
myMatrix.Translate(5.0f, 0.0f, MatrixOrderAppend);

Ilustrasi berikut menunjukkan matriks.