Procedura dettagliata: moltiplicazione di matrici

Questa procedura dettagliata illustra come usare C++ AMP per accelerare l'esecuzione della moltiplicazione di matrici. Vengono presentati due algoritmi, uno senza tiling e uno con tiling.

Prerequisiti

Prima di iniziare:

• Leggere Panoramica di C++ AMP.
• Leggere Uso dei riquadri.
• Assicurarsi di eseguire almeno Windows 7 o Windows Server 2008 R2.

Nota

Le intestazioni C++ AMP sono deprecate a partire da Visual Studio 2022 versione 17.0. L'inclusione di eventuali intestazioni AMP genererà errori di compilazione. Definire _SILENCE_AMP_DEPRECATION_WARNINGS prima di includere eventuali intestazioni AMP per disattivare gli avvisi.

Per creare il progetto

Le istruzioni per la creazione di un nuovo progetto variano a seconda della versione di Visual Studio installata. Per visualizzare la documentazione relativa alla versione preferita di Visual Studio, usare il controllo selettore della versione . Si trova nella parte superiore del sommario in questa pagina.

Per creare il progetto in Visual Studio

1. Sulla barra dei menu scegliere File>Nuovo>Progetto per aprire la finestra di dialogo Crea nuovo progetto.

2. Nella parte superiore della finestra di dialogo impostare Linguaggio su C++ , impostare Piattaforma su Windows e impostare Tipo di progetto su Console.

3. Nell'elenco filtrato dei tipi di progetto scegliere Progetto vuoto e quindi scegliere Avanti. Nella pagina successiva immettere MatrixMultiply nella casella Nome per specificare un nome per il progetto e specificare il percorso del progetto, se necessario.

   

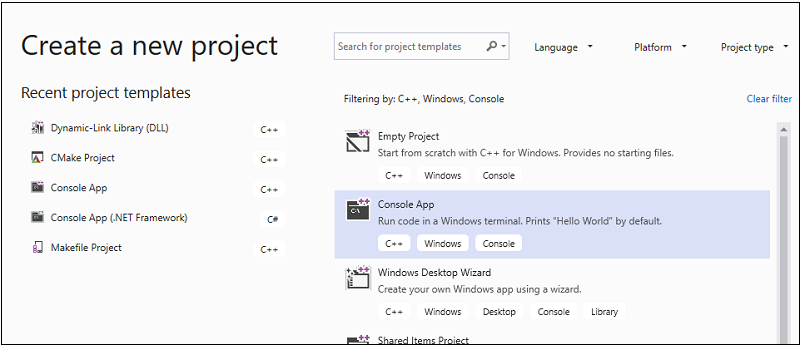
4. Scegliere il pulsante Crea per creare il progetto client.

5. In Esplora soluzioni aprire il menu di scelta rapida per File di origine e quindi scegliere Aggiungi>nuovo elemento.

6. Nella finestra di dialogo Aggiungi nuovo elemento selezionare File C++ (.cpp), immettere MatrixMultiply.cpp nella casella Nome e quindi scegliere il pulsante Aggiungi.

Moltiplicazione senza tiling

In questa sezione si consideri la moltiplicazione di due matrici, A e B, definite come segue:

Un è una matrice da 3 a 2 e B è una matrice da 2 a 3. Il prodotto della moltiplicazione A per B è la seguente matrice di 3 per 3. Il prodotto viene calcolato moltiplicando le righe di A per le colonne dell'elemento B per elemento.

Per moltiplicare senza usare C++ AMP

1. Aprire MatrixMultiply.cpp e usare il codice seguente per sostituire il codice esistente.

   #include <iostream>
   
   void MultiplyWithOutAMP() {
       int aMatrix[3][2] = {{1, 4}, {2, 5}, {3, 6}};
       int bMatrix[2][3] = {{7, 8, 9}, {10, 11, 12}};
       int product[3][3] = {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}};
   
       for (int row = 0; row < 3; row++) {
           for (int col = 0; col < 3; col++) {
               // Multiply the row of A by the column of B to get the row, column of product.
               for (int inner = 0; inner < 2; inner++) {
                   product[row][col] += aMatrix[row][inner] * bMatrix[inner][col];
               }
               std::cout << product[row][col] << "  ";
           }
           std::cout << "\n";
       }
   }
   
   int main() {
       MultiplyWithOutAMP();
       getchar();
   }
   

   L'algoritmo è un'implementazione semplice della definizione della moltiplicazione della matrice. Non usa algoritmi paralleli o thread per ridurre il tempo di calcolo.

2. Sulla barra dei menu scegliere File>Salva tutto.

3. Scegliere il tasto di scelta rapida F5 per avviare il debug e verificare che l'output sia corretto.

4. Scegliere Invio per uscire dall'applicazione.

Per moltiplicare con C++ AMP

1. In MatrixMultiply.cpp aggiungere il codice seguente prima del main metodo .

   void MultiplyWithAMP() {
   int aMatrix[] = { 1, 4, 2, 5, 3, 6 };
   int bMatrix[] = { 7, 8, 9, 10, 11, 12 };
   int productMatrix[] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 };
   
   array_view<int, 2> a(3, 2, aMatrix);
   
   array_view<int, 2> b(2, 3, bMatrix);
   
   array_view<int, 2> product(3, 3, productMatrix);
   
   parallel_for_each(product.extent,
      [=] (index<2> idx) restrict(amp) {
          int row = idx[0];
          int col = idx[1];
          for (int inner = 0; inner <2; inner++) {
              product[idx] += a(row, inner)* b(inner, col);
          }
      });
   
   product.synchronize();
   
   for (int row = 0; row <3; row++) {
      for (int col = 0; col <3; col++) {
          //std::cout << productMatrix[row*3 + col] << "  ";
          std::cout << product(row, col) << "  ";
      }
      std::cout << "\n";
     }
   }
   

   Il codice AMP è simile al codice non AMP. La chiamata a parallel_for_each avvia un thread per ogni elemento in product.extente sostituisce i for cicli per riga e colonna. Il valore della cella nella riga e nella colonna è disponibile in idx. È possibile accedere agli elementi di un array_view oggetto usando l'operatore [] e una variabile di indice oppure l'operatore () e le variabili di riga e colonna. Nell'esempio vengono illustrati entrambi i metodi. Il array_view::synchronize metodo copia nuovamente i valori della product variabile nella productMatrix variabile.

2. Aggiungere le istruzioni e using seguenti include nella parte superiore di MatrixMultiply.cpp.

   #include <amp.h>
   using namespace concurrency;
   

3. Modificare il main metodo per chiamare il MultiplyWithAMP metodo .

   int main() {
       MultiplyWithOutAMP();
       MultiplyWithAMP();
       getchar();
   }
   

4. Premere il tasto di scelta rapida CTRL+F5 per avviare il debug e verificare che l'output sia corretto.

5. Premere la barra spaziatrice per uscire dall'applicazione.

Moltiplicazione con tiling

L'associazione è una tecnica in cui si partizionano i dati in subset di dimensioni uguali, noti come riquadri. Tre cose cambiano quando si usa la tiling.

• È possibile creare tile_static variabili. L'accesso ai dati nello tile_static spazio può essere più veloce rispetto all'accesso ai dati nello spazio globale. Viene creata un'istanza di una tile_static variabile per ogni riquadro e tutti i thread nel riquadro hanno accesso alla variabile. Il vantaggio principale della tiling è il miglioramento delle prestazioni dovuto all'accesso tile_static .

• È possibile chiamare il metodo tile_barrier::wait per arrestare tutti i thread in un riquadro in una riga di codice specificata. Non è possibile garantire l'ordine in cui verranno eseguiti i thread, ma solo che tutti i thread in un riquadro si arresteranno alla chiamata a tile_barrier::wait prima di continuare l'esecuzione.

• È possibile accedere all'indice del thread rispetto all'intero array_view oggetto e all'indice relativo al riquadro. Usando l'indice locale, è possibile semplificare la lettura e il debug del codice.

Per sfruttare i vantaggi dell'associazione nella moltiplicazione di matrici, l'algoritmo deve partizionare la matrice in riquadri e quindi copiare i dati del riquadro in tile_static variabili per un accesso più rapido. In questo esempio la matrice viene partizionata in sottomatrici di dimensioni uguali. Il prodotto viene trovato moltiplicando le sottomatrici. Le due matrici e il relativo prodotto in questo esempio sono:

Le matrici vengono partizionate in quattro matrici 2x2, definite come segue:

Il prodotto di A e B può ora essere scritto e calcolato come segue:

Poiché le a matrici attraverso h sono matrici 2x2, tutti i prodotti e le somme sono anche matrici 2x2. Segue anche che il prodotto di A e B è una matrice 4x4, come previsto. Per controllare rapidamente l'algoritmo, calcolare il valore dell'elemento nella prima riga, prima colonna del prodotto. Nell'esempio, che sarebbe il valore dell'elemento nella prima riga e nella prima colonna di ae + bg. È necessario calcolare solo la prima colonna, la prima riga di ae e bg per ogni termine. Tale valore per ae è (1 * 1) + (2 * 5) = 11. Il valore per bg è (3 * 1) + (4 * 5) = 23. Il valore finale è 11 + 23 = 34, che è corretto.

Per implementare questo algoritmo, il codice:

• Usa un tiled_extent oggetto anziché un extent oggetto nella parallel_for_each chiamata.

• Usa un tiled_index oggetto anziché un index oggetto nella parallel_for_each chiamata.

• Crea tile_static variabili per contenere le sottomatrici.

• Usa il tile_barrier::wait metodo per arrestare i thread per il calcolo dei prodotti delle sottomatrici.

Per moltiplicare usando AMP e tiling

1. In MatrixMultiply.cpp aggiungere il codice seguente prima del main metodo .

   void MultiplyWithTiling() {
       // The tile size is 2.
       static const int TS = 2;
   
       // The raw data.
       int aMatrix[] = { 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 };
       int bMatrix[] = { 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 };
       int productMatrix[] = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
   
       // Create the array_view objects.
       array_view<int, 2> a(4, 4, aMatrix);
       array_view<int, 2> b(4, 4, bMatrix);
       array_view<int, 2> product(4, 4, productMatrix);
   
       // Call parallel_for_each by using 2x2 tiles.
       parallel_for_each(product.extent.tile<TS, TS>(),
           [=] (tiled_index<TS, TS> t_idx) restrict(amp)
           {
               // Get the location of the thread relative to the tile (row, col)
               // and the entire array_view (rowGlobal, colGlobal).
               int row = t_idx.local[0];
               int col = t_idx.local[1];
               int rowGlobal = t_idx.global[0];
               int colGlobal = t_idx.global[1];
               int sum = 0;
   
               // Given a 4x4 matrix and a 2x2 tile size, this loop executes twice for each thread.
               // For the first tile and the first loop, it copies a into locA and e into locB.
               // For the first tile and the second loop, it copies b into locA and g into locB.
               for (int i = 0; i < 4; i += TS) {
                   tile_static int locA[TS][TS];
                   tile_static int locB[TS][TS];
                   locA[row][col] = a(rowGlobal, col + i);
                   locB[row][col] = b(row + i, colGlobal);
                   // The threads in the tile all wait here until locA and locB are filled.
                   t_idx.barrier.wait();
   
                   // Return the product for the thread. The sum is retained across
                   // both iterations of the loop, in effect adding the two products
                   // together, for example, a*e.
                   for (int k = 0; k < TS; k++) {
                       sum += locA[row][k] * locB[k][col];
                   }
   
                   // All threads must wait until the sums are calculated. If any threads
                   // moved ahead, the values in locA and locB would change.
                   t_idx.barrier.wait();
                   // Now go on to the next iteration of the loop.
               }
   
               // After both iterations of the loop, copy the sum to the product variable by using the global location.
               product[t_idx.global] = sum;
           });
   
       // Copy the contents of product back to the productMatrix variable.
       product.synchronize();
   
       for (int row = 0; row <4; row++) {
           for (int col = 0; col <4; col++) {
               // The results are available from both the product and productMatrix variables.
               //std::cout << productMatrix[row*3 + col] << "  ";
               std::cout << product(row, col) << "  ";
           }
           std::cout << "\n";
       }
   }
   

   Questo esempio è significativamente diverso rispetto all'esempio senza affiancamento. Il codice usa questi passaggi concettuali:

   1. Copiare gli elementi del riquadro[0,0] di a in locA. Copiare gli elementi del riquadro[0,0] di b in locB. Si noti che product è affiancato, non a e b. Pertanto, si usano indici globali per accedere a, ba e product. La chiamata a tile_barrier::wait è essenziale. Arresta tutti i thread nel riquadro fino a quando non vengono riempiti entrambi locA e locB .

   2. Moltiplicare locA e locB inserire i risultati in product.

   3. Copiare gli elementi del riquadro[0,1] di a in locA. Copiare gli elementi del riquadro [1,0] di b in locB.

   4. Moltiplicare locA e locB aggiungerli ai risultati già presenti in product.

   5. La moltiplicazione del riquadro[0,0] è completata.

   6. Ripetere per gli altri quattro riquadri. Non esiste alcuna indicizzazione specifica per i riquadri e i thread possono essere eseguiti in qualsiasi ordine. Durante l'esecuzione di ogni thread, le tile_static variabili vengono create per ogni riquadro in modo appropriato e la chiamata per tile_barrier::wait controllare il flusso del programma.

   7. Quando si esamina attentamente l'algoritmo, si noti che ogni submatrix viene caricato in una tile_static memoria due volte. Il trasferimento dei dati richiede tempo. Tuttavia, una volta che i dati sono in tile_static memoria, l'accesso ai dati è molto più veloce. Poiché il calcolo dei prodotti richiede l'accesso ripetuto ai valori nelle sottomatrici, esiste un miglioramento complessivo delle prestazioni. Per ogni algoritmo, la sperimentazione è necessaria per trovare l'algoritmo e le dimensioni del riquadro ottimali.

   Negli esempi non AMP e non affiancati, ogni elemento di A e B è accessibile quattro volte dalla memoria globale per calcolare il prodotto. Nell'esempio di riquadro ogni elemento è accessibile due volte dalla memoria globale e quattro volte dalla tile_static memoria. Questo non è un miglioramento significativo delle prestazioni. Tuttavia, se le matrici A e B erano 1024x1024 e le dimensioni del riquadro erano 16, ci sarebbe un miglioramento significativo delle prestazioni. In tal caso, ogni elemento verrà copiato in tile_static memoria solo 16 volte e accessibile dalla tile_static memoria 1024 volte.

2. Modificare il metodo main per chiamare il MultiplyWithTiling metodo , come illustrato.

   int main() {
       MultiplyWithOutAMP();
       MultiplyWithAMP();
       MultiplyWithTiling();
       getchar();
   }
   

3. Premere il tasto di scelta rapida CTRL+F5 per avviare il debug e verificare che l'output sia corretto.

4. Premere la barra spaziatrice per uscire dall'applicazione.

Vedi anche

C++ AMP (C++ Accelerated Massive Parallelism)
Procedura dettagliata: debug di un'applicazione C++ AMP