Applicazione di trasformazioni in Direct2D

In Disegno con Direct2Dè stato rilevato che il metodo ID2D1RenderTarget::FillEllipse disegna un'ellisse allineata agli assi x e y. Ma si supponga di voler disegnare un'ellisse inclinata in un angolo?

Utilizzando le trasformazioni, è possibile modificare una forma nei modi seguenti.

• Rotazione intorno a un punto.
• Scalabilità.
• Traslazione (spostamento nella direzione X o Y).
• Asimmetria (nota anche come taglio ).

Una trasformazione è un'operazione matematica che trasforma un insieme di punti in un nuovo insieme di punti. Ad esempio, il diagramma seguente mostra un triangolo ruotato intorno al punto P3. Dopo l'applicazione della rotazione, il punto P1 viene mappato a P1', il punto P2 viene mappato a P2' e il punto P3 esegue il mapping a se stesso.

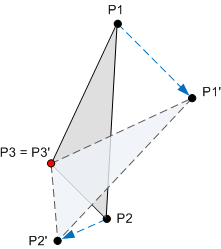
Le trasformazioni vengono implementate usando matrici. Tuttavia, non è necessario comprendere la matematica delle matrici per usarle. Per altre informazioni sulla matematica, vedere Appendice: Trasformazioni di matrice.

Per applicare una trasformazione in Direct2D, chiamare il metodo ID2D1RenderTarget::SetTransform. Questo metodo accetta una struttura D2D1_MATRIX_3X2_F che definisce la trasformazione. È possibile inizializzare questa struttura chiamando i metodi nella classe D2D1::Matrix3x2F. Questa classe contiene metodi statici che restituiscono una matrice per ogni tipo di trasformazione:

• Matrix3x2F::Rotation
• Matrix3x2F::Scale
• Matrix3x2F::Translation
• Matrix3x2F::Skew

Ad esempio, il codice seguente applica una rotazione di 20 gradi intorno al punto (100, 100).

pRenderTarget->SetTransform(
    D2D1::Matrix3x2F::Rotation(20, D2D1::Point2F(100,100)));

La trasformazione viene applicata a tutte le operazioni di disegno successive fino a quando non si chiama di nuovo SetTransform. Per rimuovere la trasformazione corrente, chiamare SetTransform con la matrice di identità. Per creare la matrice di identità, chiamare la funzione Matrix3x2F::Identity.

pRenderTarget->SetTransform(D2D1::Matrix3x2F::Identity());

Disegno delle lancette dell'orologio

Utilizziamo le trasformazioni convertendo il nostro programma Circle in un orologio analogico. Possiamo farlo aggiungendo linee per le mani.

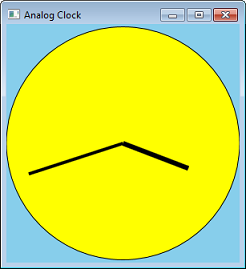
Anziché calcolare le coordinate per le linee, è possibile calcolare l'angolo e quindi applicare una trasformazione di rotazione. Il codice seguente mostra una funzione che disegna una mano dell'orologio. Il parametro fAngle fornisce l'angolo della mano, espresso in gradi.

void Scene::DrawClockHand(float fHandLength, float fAngle, float fStrokeWidth)
{
    m_pRenderTarget->SetTransform(
        D2D1::Matrix3x2F::Rotation(fAngle, m_ellipse.point)
            );

    // endPoint defines one end of the hand.
    D2D_POINT_2F endPoint = D2D1::Point2F(
        m_ellipse.point.x,
        m_ellipse.point.y - (m_ellipse.radiusY * fHandLength)
        );

    // Draw a line from the center of the ellipse to endPoint.
    m_pRenderTarget->DrawLine(
        m_ellipse.point, endPoint, m_pStroke, fStrokeWidth);
}

Questo codice disegna una linea verticale, a partire dal centro del viso dell'orologio e termina nel punto endPoint. La linea viene ruotata intorno al centro dell'ellisse applicando una trasformazione di rotazione. Il punto centrale per la rotazione è il centro dell'ellisse che forma la faccia dell'orologio.

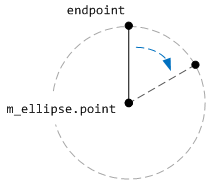
Il codice seguente mostra come viene disegnato l'intero viso dell'orologio.

void Scene::RenderScene()
{
    m_pRenderTarget->Clear(D2D1::ColorF(D2D1::ColorF::SkyBlue));

    m_pRenderTarget->FillEllipse(m_ellipse, m_pFill);
    m_pRenderTarget->DrawEllipse(m_ellipse, m_pStroke);

    // Draw hands
    SYSTEMTIME time;
    GetLocalTime(&time);

    // 60 minutes = 30 degrees, 1 minute = 0.5 degree
    const float fHourAngle = (360.0f / 12) * (time.wHour) + (time.wMinute * 0.5f);
    const float fMinuteAngle =(360.0f / 60) * (time.wMinute);

    DrawClockHand(0.6f,  fHourAngle,   6);
    DrawClockHand(0.85f, fMinuteAngle, 4);

    // Restore the identity transformation.
    m_pRenderTarget->SetTransform( D2D1::Matrix3x2F::Identity() );
}

È possibile scaricare il progetto di Visual Studio completo da esempio di orologio Direct2D. (Solo per divertimento, la versione scaricabile aggiunge una sfumatura radiale al quadrante dell'orologio.)

Combinazione di trasformazioni

Le quattro trasformazioni di base possono essere combinate moltiplicando due o più matrici. Ad esempio, il codice seguente combina una rotazione con una traslazione.

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(20);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(40, 10);

pRenderTarget->SetTransform(rot * trans);

La classe Matrix3x2F fornisceoperator*()per la moltiplicazione della matrice. L'ordine in cui si moltiplicano le matrici è importante. L'impostazione di una trasformazione (M × N) significa "Applica prima M, seguita da N". Ad esempio, ecco la rotazione seguita dalla traduzione:

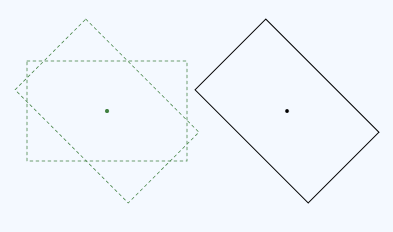
Ecco il codice per questa trasformazione:

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(rot * trans);

Confrontare ora la trasformazione con una trasformazione nell'ordine inverso, la traslazione seguita dalla rotazione.

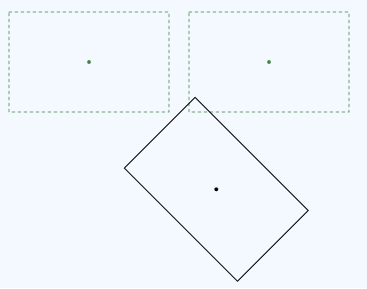
La rotazione viene eseguita intorno al centro del rettangolo originale. Ecco il codice per questa trasformazione.

D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(trans * rot);

Come si può notare, le matrici sono le stesse, ma l'ordine delle operazioni è cambiato. Ciò si verifica perché la moltiplicazione della matrice non è commutativa: M × N ≠ N × M.

Prossimo

Appendice : Trasformazioni matrici