Silverlight
Building Advanced 3D Animations with Silverlight 2.0
Declan Brennan
Code download available at:SilverlightAnimation2008_04.exe(228 KB)
This article discusses:
|
This article uses the following technologies: Silverlight |
Contents
Using XAML
Some XAML Examples
Tips for Working with XAML
How to Fold a Polyhedron
Emulating DirectX Math
More to Explore
If, by some incredible mischance, all the publicity in the past few months about SilverlightTM has passed you by, let me bring you up to date: Silverlight is a new cross-browser plug-in from Microsoft that brings the power of the Microsoft® .NET Framework to bear on an area that was previously reserved for Flash or Java Applets. Silverlight has a wealth of useful features out of the box. It supports a lean-and-mean version of the .NET Framework 3.5 that includes, among other things, XML and Extensible Application Markup Language (XAML), generic collections, Web services, and LINQ. Silverlight also supports a range of .NET-compliant languages, but here I'll be sticking to C#.
I think the best way to come to grips with a new technology is to have a little fun with it. So when the Silverlight 1.1 alpha was released and I saw the exciting presentation by Tim Sneath at the IMT conference in Dublin, I decided to throw together a little educational application demonstrating how various 3D shapes (called polyhedra) can be assembled by folding a flat template. Silverlight doesn't support 3D by default, so this involved building an emulation of the DirectX® math libraries to do the 3D stuff.
A polyhedron is a three-dimensional object with flat faces. This Silverlight sample explores those regular and semi-regular polyhedra called the Platonic and Archimedian polyhedra. The faces of these polyhedra are all regular polygons—their sides are all the same length—such as equilateral triangles or squares. They are also convex, meaning they have no pieces that stick out. As you might guess from the ancient Greek names, these objects have fascinated humanity for a long time. If you're interested, you can find out a lot more about them on George Hart's Web site: georgehart.com/virtual-polyhedra/vp.html.
You can see a demo of the finished application in Figure 1 or at picturespice.com/ps/Polyhedra/default.html. Basically, the application allows you to select a shape (a polyhedron) by moving the mouse over it. You are then presented with some information about your selection in the top-right corner of the window and also an animation of a flat template folding to form your chosen polyhedron. Finally, if you click the Cycle button, the program automatically cycles through each of the shapes in turn.
Figure 1** Silverlight Demonstration of Polyhedra **
Using XAML
Like many Silverlight applications, Polyhedra makes heavy use of XAML, which is a content definition language—a sort of HTML equivalent, but more flexible. Continuing the analogy, while it is possible to create an HTML page using only the HTML document object model (DOM), this is rarely a sensible way to produce content—it's often time-consuming to code, and it produces pages that are slow to initialize. It's nearly always best to keep as much of the page as possible as HTML markup and then augment this using JavaScript and the DOM where flexibility is needed.
A very similar approach applies to XAML. The fastest way to get content together is to use XAML markup as much as possible and augment this where necessary using a .NET-compliant language such as C# and the Silverlight Media API. The XAML may be hand coded, produced by a design package such as Expression BlendTM, generated from a program that is run during the development process, or even dynamically generated on the server. This can require a change of mind-set. It's all too easy as a C# programmer to end up coding functionality in your natural environment that is best left to XAML.
Anything but a very brief taste of XAML would be beyond the scope of this article. However, Charles Petzold covers XAML in great detail in his book Applications= Code+Markup.
Here's the XAML equivalent of the "Hello World" example that we've all come to expect when learning new languages:
<UserControl x:Class="Polyhedra.Page"
xmlns="https://schemas.microsoft.com/client/2007"
xmlns:x="https://schemas.microsoft.com/winfx/2006/xaml"
Width="400" Height="300">
<Grid x:Name="LayoutRoot" Background="White">
<TextBlock>Hello World</TextBlock>
</Grid>
</UserControl>
The root element is a UserControl. This contains a Grid, which, in turn, contains a TextBlock element with the "Hello World" text.
Have a quick look at the UserControl attributes. Without going into too much detail, this defines the equivalent of a codebehind class for the XAML. This class is instantiated at the same time that the XAML is parsed and loaded. You can perform various bits of initialization in the constructor, but to get more elaborate behavior it is often necessary to employ event handlers. This is a key feature of Silverlight. Event handlers can be attached to various XAML objects and implemented in the .NET-compliant language of your choice—a language that, unlike JavaScript, is compiled and therefore opens up all sorts of possibilities that would be otherwise impractical.
Returning to the HTML analogy, elements are often grouped inside various DIVs to arrange their location on the page. Similarly, in XAML, the shapes are grouped inside Canvases (or other elements such as Grids that are types of Canvas). Just as DIVs are often nested in HTML, so Canvases can be nested in XAML. Most elements in HTML are rectangular. However, XAML supports a whole range of shapes including TextBlock, Rectangle, Polygon, Ellipse, and the very flexible Path, which allows for user-defined shapes. Elements in HTML are identified with an ID attribute, and the equivalent attribute to identify an element in XAML is x:Name, where x is the alias for the XAML namespace.
XAML does a lot more than just produce static pages. One of its most powerful features is the use of storyboards as a way to animate changes to the initial UI specified by the XAML. (Something similar, called HTML+Time, was added to HTML in Internet Explorer® 5.0) An example might be to animate a change to the color, visibility, or transparency of an object. If used in conjunction with transforms, storyboards can also rotate, scale, or move objects.
Storyboards can generate all sorts of animation effects with little or no conventional code. When used in conjunction with triggers, it is, in theory, possible to start various animations automatically when an event such as MouseEnter occurs on an object. Alas, as of the March 2008 Silverlight 2.0 Beta,, the only event handled by a trigger is Loaded. For other events, a small amount of plumbing code is required in the form of an event handler. I expect this situation will change soon, if it hasn't already done so.
One nice feature of storyboards in Silverlight is that they are time-based rather than frame-based. Using multiple independent storyboards tied to different times and events can make a complex behavior simple to implement. After all, the real world doesn't operate in frames—it's a hangover from the way that moving pictures were achieved on celluloid. If independent objects are implemented with independent behaviors, it makes for a far simpler life.
Some XAML Examples
The folding animation in the middle of the Polyhedra application is generated using C# code. However, the bulk of the remainder is defined in XAML. This includes the circle of sample polyhedra, the way the currently selected polyhedron is emphasized in a variety of ways, and the Cycle button, which shows that it is activated by animating a rotating arrow.
Let's look at a couple of excerpts from Page.xaml to see how these animations are achieved, starting with a look at the Cycle button, shown in Figure 2. Have a look at the Path named Cycle. The data attribute specifies a series of operations including M for move, A for arc, and L for line. As this is a pretty simple glyph, I just drew the shape I wanted on a sheet of paper and manually worked out the operations required. In most cases, you'll be better off using a tool for this such as Expression Design.
Figure 2 Cycle Button
<Canvas x:Name="CycleButton"
Canvas.Top="250"
MouseLeftButtonDown="CycleButtonLeftMouseDown" >
<Path x:Name="Cycle" Stroke="#000033"
Fill="#FFB47C0D" Canvas.Left="10" Canvas.Top="10"
Data="M 25,35 A 10,10 180 1 0 25,15 L 25,20 L 12.5,10 L 25,0 L 25,
5 A 10,10 180 1 1 25,45 Z"
Width="50" Height="50">
<Path.RenderTransform>
<RotateTransform x:Name="CycleRotate" Angle="0"
CenterX="25" CenterY="25"/>
</Path.RenderTransform>
<Path.Resources>
<Storyboard x:Name="CycleLatched">
<DoubleAnimation Storyboard.TargetName="CycleRotate"
Storyboard.TargetProperty="Angle" From="360" To="0"
Duration="00:00:02" RepeatBehavior="Forever"/>
</Storyboard>
</Path.Resources>
</Path>
<TextBlock x:Name="CycleCaption" Canvas.Left="65" Canvas.Top="10"
Foreground="#FFB47C0D" FontSize="30" FontWeight="Bold"
Text="Cycle" />
<Rectangle Width="200" Height="70" RadiusX="30" RadiusY="30"
Stroke="#FFB47C0D" StrokeThickness="4" Fill="Transparent"/>
</Canvas>
This Path also has a RotateTransform named CycleRotate. Initially, this transform does nothing, as its angle is set to 0. However, there is a Storyboard named CycleLatched that, when active, continuously changes the angle in small increments, which causes the arrow to rotate.
Figure 3 shows how one of the polyhedron samples is defined. At the bottom of this XAML, you can see that the sample consists of the four Polygons that define the tetrahedron. They are inside their own Canvas, called Model0, and are surrounded by a ring or Ellipse called Ring0 that is initially invisible. There are two Storyboard animations defined, one for MouseEnter and one for MouseLeave. The MouseEnter animation makes the ring visible immediately, inflates the size of the Model0 canvas, and makes it more opaque over a period of .7 seconds. The MouseLeave animation reverses each of these changes.
Figure 3 Polyhedron Sample
<Canvas x:Name="Canvas0" Width="116.376" Height="116.376"
Canvas.Left="671.812" Canvas.Top="341.812"
MouseEnter="TriggerMouseEnter" MouseLeave="TriggerMouseLeave">
<Canvas.Resources>
<Storyboard x:Name="Canvas0MouseEnter">
<DoubleAnimation Duration="00:00:00" Storyboard.TargetName="Ring0"
Storyboard.TargetProperty="Opacity" From="0.0" To="1.0" />
<DoubleAnimation Duration="00:00:00.7"
Storyboard.TargetName="Model0"
Storyboard.TargetProperty="Opacity" From="0.7" To="1.0" />
<DoubleAnimation Duration="00:00:00.7"
Storyboard.TargetName="Model0Scale"
Storyboard.TargetProperty="ScaleX" From="0.7" To="1.0" />
<DoubleAnimation Duration="00:00:00.7"
Storyboard.TargetName="Model0Scale"
Storyboard.TargetProperty="ScaleY" From="0.7" To="1.0" />
</Storyboard>
<Storyboard x:Name="Canvas0MouseLeave">
<DoubleAnimation Duration="00:00:00" Storyboard.TargetName="Ring0"
Storyboard.TargetProperty="Opacity" From="1.0" To="0.0" />
<DoubleAnimation Duration="00:00:00.7"
Storyboard.TargetName="Model0"
Storyboard.TargetProperty="Opacity" From="1.0" To="0.7" />
<DoubleAnimation Duration="00:00:00.7"
Storyboard.TargetName="Model0Scale"
Storyboard.TargetProperty="ScaleX" From="1.0" To="0.7" />
<DoubleAnimation Duration="00:00:00.7"
Storyboard.TargetName="Model0Scale"
Storyboard.TargetProperty="ScaleY" From="1.0" To="0.7" />
</Storyboard>
</Canvas.Resources>
<Canvas x:Name="Model0" Opacity="0.7"
Width="116.376" Height="116.376" >
<Canvas.RenderTransform>
<ScaleTransform x:Name="Model0Scale" CenterX="58.188"
CenterY="58.188" ScaleX="0.7" ScaleY="0.7"/>
</Canvas.RenderTransform>
<Polygon Canvas.ZIndex="-12545653" Fill="#FFCC0000"
Stroke="#000000" StrokeThickness="1"
Points="97.566,74.278 43.052,40.971 33.836,99.937 "/>
<Polygon Canvas.ZIndex="-11948057" Fill="#FFCC0000"
Stroke="#000000" StrokeThickness="1"
Points="43.052,40.971 97.566,74.278 58.188,37.662 "/>
<Polygon Canvas.ZIndex="-11309683" Fill="#FFCC0000"
Stroke="#000000" StrokeThickness="1"
Points="33.836,99.937 43.052,40.971 58.188,37.662 "/>
<Polygon Canvas.ZIndex="-10481036" Fill="#FFCC0000"
Stroke="#000000" StrokeThickness="1"
Points="97.566,74.278 33.836,99.937 58.188,37.662 "/>
</Canvas>
<Ellipse x:Name="Ring0" Opacity="0" Stroke="#FFB47C0D"
StrokeThickness="4" Width="116.376" Height="116.376" />
</Canvas>
Because these storyboards can operate independently, everything happens as you would expect regardless of how quickly the user moves the mouse. Typically, a MouseLeave animation for one sample will be taking place at the same time as the MouseEnter animation for the newly selected sample. However, you don't have to worry about it, as Silverlight will automatically handle running multiple active storyboards in parallel.
As a slight aside, you may be wondering how the corners of each of the four Polygons for the tetrahedron sample were calculated, not to mention the often far larger number of Polygons for each of the other samples in the application. I'm a big believer in the lazy approach of never doing anything yourself that a computer can do quicker. So all I did was use a modified version of Polyhedra during the production process. This version performed one frame of the central animation for each of the samples in turn—the frame with the fully closed shape. I placed each of the resulting Polygon groups in a set of Canvases that were equally spaced around a circle and streamed the whole lot to a file for use by the main program.
Laying objects around a circle involves stepping the angle up in equal increments of 2*PI/NumSamples and then specifying the center of each sample using a coordinate of x= Radius*Cos(Angle), y=Radius*Sin(Angle). Also, because the canvas positioning objects use Left and Top properties, I needed to offset the center by half the width and half the height, respectively.
Tips for Working with XAML
As you can see, it's possible to achieve quite a rich UI with XAML and almost no additional code. Even for a large file like Page.xaml, initialization is surprisingly quick. But before I move on, here are a few tips based on my experiences with the current implementation (March 2008 Beta) of Silverlight 2.0.
As I've already mentioned, currently triggers can only start a storyboard automatically (via the Begin method) for the Loaded event. For other events, a small amount of plumbing code is required in the form of an event handler like this:
public void MouseEnterHandler(
object o, EventArgs e) {
this.MouseEnterStoryBoard.Begin();
}
If you adopt a naming convention for your storyboards, such as the object name followed by the event name, you can cut down greatly on the number of separate event handlers that you need to code. For example, this method is used in Polyhedra as a shared event handler for all the samples in the circle:
public void MouseEnterHandler(
object o, EventArgs e) {
this.triggerStoryboard(o,"MouseEnter");
}
private bool triggerStoryboard(
object o, string eventType) {
Canvas el = o as Canvas;
string name= el.GetValue(NameProperty) as String;
Storyboard sb = el.FindName(name + eventType) as Storyboard;
if (sb != null)
sb.Begin();
return (sb != null);
}
With the Silverlight 2.0 Beta, the main initialization (calling InitComponents) has moved from a Loaded event handler to the constructor for the codebehind object. This is more elegant, but beware that not everything is possible in the constructor. For example, it's not possible to call Begin or Pause on a storyboard here, so this will still need to be done in an event handler.
As I discovered from Andy Beaulieu's asteroid-blasting Silverlight Rocks! sample (www.andybeaulieu.com/Home/tabid/67/EntryID/73/default.aspx), a good way to achieve a code-based animation is to use a storyboard set to a short time period and have a Completed event handler that does a frame of animation and then restarts the storyboard:
public Page() { // Constructor for "code-behind"
// Required to initialize variables
InitializeComponent();
this.animationTimer.Completed +=
new EventHandler(animationTimer_Completed);
}
void animationTimer_Completed(object sender, EventArgs e) {
[ Do a frame of animation ]
this.animationTimer.Begin();
}
The September Refresh of the Silverlight 2.0 Alpha changed the requirements for storyboards so that an animation must now have a target even if it's not used:
<Canvas.Resources>
<Storyboard x:Name="animationTimer">
<DoubleAnimation Duration="00:00:00.01"
Storyboard.TargetName="bogusTimerTarget"
Storyboard.TargetProperty="Width" />
</Storyboard>
</Canvas.Resources>
<Canvas Name="bogusTimerTarget">
</Canvas>
Don't try to have lots of separate Silverlight controls on the same HTML page. My first implementation of Polyhedra used a separate control for each sample in the circle, and it was a real memory hog. This may, in some cases, mean moving content from HTML to XAML to cut down on the number of controls you are using.
One of the advantages of XAML is that it offloads a lot of the routine stuff in the UI, allowing you to concentrate on the creative problem domain code. In this example, the problem domain involves the folding of templates to form the 3D shapes, which leads us to the next section.
How to Fold a Polyhedron
I suspect that Charles Petzold's book, mentioned earlier, is an adaptation of a far older, pre-object-oriented book by Niklaus Wirth called Algorithms+Data Structures=Programs. Even after all these years, it remains one of the most influential books that I have ever read, and, despite all the changes in languages and paradigms that have taken place since then, it is still highly relevant. The basic tenet of the book is an approach to development that consists of identifying what data structures can best model your problem, then identifying what algorithms can process or modify these data structures. When tackling a non-standard program, this is an approach that I often adopt.
I played around with various approaches before settling on the one finally used in Polyhedra. I wanted to see how little information I could practically start with to achieve the folding animation. It turns out that, since all the sides are the same length, it's almost possible to do everything just from the knowledge of which faces are connected to which in a given polyhedron. This suggests a graph data structure. Before reaching the final XAML output, a set of algorithms are used to process the graph through two separate tree data structures. All of this will be explained later.
Although Windows® Presentation Foundation (WPF) can support 3D in XAML, Silverlight only supports 2D by default because cross-browser compatibility is far easier to achieve when you don't have to worry about what Graphics Processing Unit (GPU) hardware is in the machine. Of course, when you get down to it, 3D on a computer screen is an illusion. Regardless of what manipulations take place, in the end a set of ordinary 2D polygons is being displayed on the monitor surface. If you are willing to do the 3D manipulations in your own code to calculate the coordinates of these polygons, a non-hardware-accelerated 3D rendering is possible. Provided you restrict yourself to a few dozen polygons, the performance is acceptable. (Subjectively, frame performance has improved moving from the Alpha to the Beta.)
When a shape is selected, a two-dimensional unfolded template called a Net (nothing to do with .NET) is built. This is done in two phases, as illustrated in Figure 4. First a graph is built in memory with one GraphNode corresponding to each face in the shape (see Graph.cs). This graph is built by streaming in a set of connectivity information (indicating which face is connected to which faces) from one of the .shp resources that are embedded in the application assembly. For example, here are the contents of cube.shp:

Figure 4** Building the Shape, from Graph to XAML **(Click the image for a larger view)
1:3,4,5,2
2:1,5,6,3
3:2,6,4,1
4:3,6,5,1
5:1,4,6,2
6:2,5,4,3
Any GraphNode in the graph can then be chosen as the first node from which to start building the Net (see Net.cs in the code download for details). A two-dimensional FlatFace is then laid out with the same number of sides as the GraphNode has neighbors. Any neighboring GraphNode is then chosen to repeat the process, laying out the next FlatFace so it shares a side with the current one. Each GraphNode is only visited once, and the process continues until all GraphNodes have been visited, resulting in a tree structure of FlatFaces.
In each frame of the 3D animation, a three-dimensional polyhedron (possibly partially closed) is built from the Net (see Polyhedron.cs later in this article for the details of this operation). This involves copying the tree of FlatFaces into a tree of Faces replacing 2D corner points with 3D points. (Figure 5 shows the two coordinate systems. Because I want to start in the horizontal plane, Y should start as zero. So I map from 2D to 3D by setting X=X, Y=0, and Z=Y.)
Figure 5** Transforming Points from 2D to 3D **(Click the image for a larger view)
Finally, recursion is used to visit each join in the tree of Faces to perform a fold. The amount of the fold is a fraction of the angle (called a dihedral angle) that the faces will have to each other when the shape is fully closed. It is, in theory, possible to calculate the dihedral angles directly using just the connectivity information in the .shp file.
This is fairly easy for special cases such as any three faces meeting at a corner or any number of faces of the same type meeting at a corner. However the general case is somewhat more difficult, so I decided to store these angles in separate .dihedrals resources. For example, here's an excerpt from cube.dihedrals:
1,3:1.5707965056551
1,4:1.57079661280793
1,5:1.57079614793469
1,2:1.57079604078186
2,1:1.57079604078186
2,5:1.57079628466395
2,6:1.57079661280793
2,3:1.57079636892585
3,2:1.57079636892585
3,6:1.57079614793469
3,4:1.57079628466395
...
The minute differences in these numbers, which should all be PI/2 in this case, are merely an artifact of the way they were calculated.
The final process involves a series of transformations to project a view of the polyhedron onto the monitor as a set of polygons. You may have noticed that, during the folding animation, the polyhedron is also rotated about a vertical axis. To achieve this, I translate the pivot point to the origin, perform the rotation, and then translate to the viewpoint. Then I do a perspective transformation to ensure that far away objects (on the Z axis) appear smaller. (I'll explain a bit more about how to do transformations in the next section.)
Finally, a set of XAML polygons is generated corresponding to the projection of the 3D shape onto the monitor's surface. Silverlight is forced to draw these polygons in back-to-front order by setting the XAML ZIndex property for each Polygon using the Z coordinate of the center of the 3D polygon (scaled to squeeze a float into an int). This is a fairly simplistic way of achieving 3D that will only work if the polygons behave themselves by, for example, not intersecting—something I can get away with in this sample. Smarter forms of 3D involve mechanisms such as depth buffers. As these require GPU access, they are out of scope for the Silverlight .NET sandbox.
As a last touch, XAML allows Polygons to be partially transparent (using the Opacity property), which gives the artistic effect of a partially see-through polyhedron. And that, as they say, is all there is to it.
Emulating DirectX Math
I'm going to touch lightly on the math used to achieve the animation. If you want to go into more detail, there are many sites on the Web that will help, including wikipedia.com, euclideanspace.com, mathworld.wolfram.com, gamasutra.com, and gamedev.net.
I have already introduced some 2D transformations, such as RotationTransform and ScaleTransform, in the XAML samples shown earlier. In these, Silverlight does all the work for you. If you use XAML in a WPF environment, you also have access to 3D transformations, but these are not available in Silverlight. WPF relies upon DirectX to do the low-level work for it. This makes sense, as DirectX has a nice set of classes for doing the math required for 3D transforms. To do some of the same transformations in Silverlight, I've produced a DirectX Math emulation of many of these classes so that they can be used in the Silverlight sandbox.
If you have any experience coding in Direct3D®, you'll be quite at home with the Microsoft implementations of Vector2, Vector3, Matrix, and the like (see Figure 6). If not, I'll give a very brief and very non-rigorous overview and some examples.
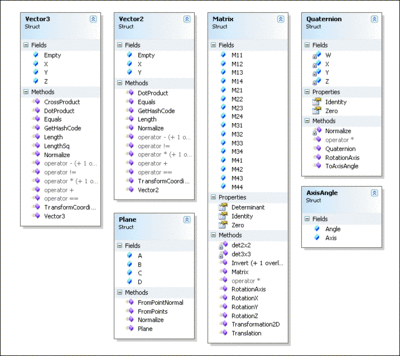
Figure 6** Emulated DirectX Math Classes **(Click the image for a larger view)
Locating a point in 2D requires two coordinates: X and Y. In 3D it requires three coordinates: X, Y, and Z. Although, strictly speaking, points are not vectors, 2D points can be stored in a Vector2 object and 3D points in a Vector3 object. (Vectors are actually entities with a magnitude and a direction, which you can illustrate by having an arrow that starts at the origin and ends at the point. In a sense, you can think of all vectors as starting from the origin.)
Shapes in three dimensions can be identified as a set of faces. Faces, in turn, are identified as a set of points corresponding to corners. Nearly everything you might want to do involves transforming these points to another set of points by applying one or more operations such as rotation, translation (or moving), or scaling. Nearly every operation that you might want to do can be represented by a 4-by-4 grid of numbers called a matrix. (Matrices in general can actually have any number of rows and columns, but we're only interested in the special ones used to manipulate 3D points with what are called homogeneous coordinates.) These operations are referred to as linear transformations because they don't (overly) distort the shape of the object they are applied to.
Very usefully, there is a way of combining two such matrices into one resulting matrix that has the same effect. This operation is called matrix multiplication and can be repeated several times. This means you can chain a whole set of transformations together into a single matrix with the same effect. This is far more efficient than applying each transformation separately. There's no need to worry about how matrix multiplication is implemented or how it does its transformation magic. Just use it as a tool.
To transform a source point into a target point, there is also a multiplication operation defined between a matrix and a vector object. To avoid confusion (with matrix-matrix multiplication), this is implemented in Vector3 using the TransformCoordinate method.
A couple of little code snippets should make things more clear. First, the following code in polyhedron.cs is used to fold two faces along their common side:
Vector3 axis = axisTo - axisFrom;
Matrix foldTransform =
Matrix.Translation(-axisFrom) *
Matrix.RotationAxis(axis, proportion * _dihedralAngle) *
Matrix.Translation(axisFrom);
Vector3[] p= Vector3.TransformCoordinate(
face.Points,foldTransform);
Here the common side is defined as a line from axisFrom to axisTo. Rotations are always defined about a line through the origin, so, before I rotate, I need to move one point of the side to the origin and then move it back afterward. To do this, I'm chaining together three linear transformations to build the matrix that I use to transform the face coordinate: move to the origin, rotate, and then move back again.
There's one other little trick here: the vector representing the axis of rotation also has to start from the origin, so I subtract axisFrom, moving (axisFrom,axisTo) to (origin, axisTo-AxisFrom).
If your head is not too full of math now, let's try one more example (based on projector.cs) that is used to transform the polygons of the polyhedron into what you would expect to see from the screen viewpoint:
Matrix projection =
Matrix.Translation(-pivot) *
Matrix.RotationY(yaw) *
Matrix.RotationX(angle) *
Matrix.Translation(viewPoint) *
Geometry.Perspective(5);
Vector3[] p= Vector3.TransformCoordinate(face.Points,foldTransform);
Remember that the shape is being rotated in the horizontal plane while it is being folded. To do this, a point on the pivot axis is moved to the origin, then a rotation takes place about the vertical (Y) axis through the yaw angle. (If you've flown an aircraft in reality or simulation, you will have come across the other two possible independent rotations called pitch and roll.)
This time, instead of moving back to the start position, a move takes place to the viewpoint. Finally, a perspective transformation takes place to shrink the stuff that is far away on the Z axis. There's a lot going on here, yet it can all be combined into a single 4-by-4 matrix, which is pretty impressive.
More to Explore
Although not used in Polyhedra, quaternions are also available in the emulation library. They are a good way to combine a set of 3D rotations into a single rotation. They are also great for smoothly changing from one orientation to another. They were discovered by Sir William Rowan Hamilton (from my hometown of Dublin, Ireland) while walking along the street, and he promptly scribbled the equation on the side of the Broome Bridge so he wouldn't forget it (go to www.maths.tcd.ie/pub/HistMath/People/Hamilton/Quaternions.html). I'd like to claim that all our graffiti is equally erudite, but I don't suppose you'd believe me.
Quaternions also avoid a problem called gimbal lock. This played an important part in gyroscope navigation during the Apollo moon missions and was featured in a movie about the Apollo 13 mission.
There's plenty of other stuff that I haven't gone into, such as vector dot products and cross products, but hopefully I've given you a flavor of what's possible with the DirectX Math emulation. I originally developed this emulation to do transformations on a hosted server running ASP.NET where I couldn't install DirectX. You may find other applications for it in this type of environment.
Polyhedron should give you a taste of how Silverlight provides a useful, extensible tool for Web UIs that really grab the user's attention and get information across in fast and memorable ways. You can build on your existing .NET experience in all sorts of creative ways, and, unlike JavaScript, you don't have to be obsessive about the number of lines of code being executed on the client.
Declan Brennan is old enough to remember the first microprocessor, and he still hasn't gotten used to having his own personal genie in a bottle. He can't believe his luck at being in a world limited not by technology but only by imagination. Learn more about Declan at declan.brennan.name.