グローバーの検索アルゴリズムの理論

この記事では、グローバーのアルゴリズムを機能させる数学的原理の詳細な理論的説明を示します。

数学的な問題を解決するためのグローバーのアルゴリズムの実際の実装については、「 グローバーの検索アルゴリズムを実装する」を参照してください。

問題のステートメント

任意の検索タスクは、検索項目 $x$ を受け取る抽象関数 $f(x)$ で表すことができます。 項目 $x$ が検索タスクの解である場合には、$f(x)=1$ です。 項目 $x$ が解でない場合は、$f(x)=0$ となります。 "検索の問題" は、$f(x_0)=1$ である任意の項目 $x_0$ を探すことで構成されます。

グローバーのアルゴリズムが解決しようとしているタスクは、次のように表すことができます。古典的関数 $f(x):\{0,1\}^n \rightarrow\{0,1\}$ が与えられ、$n$ が検索空間のビット サイズであるときに、$f(x_0)=1$ である入力 $x_0$ を探します。 アルゴリズムの複雑さは、関数 $f(x)$ の使用回数によって測定されます。 古典的には、最悪のシナリオで $f(x)$ を合計 $N-1$ 回評価してすべての可能性を試す必要があります。ここで $N=2^n$ です。 $N-1$ 要素の後、それは最後の要素である必要があります。 グローバーの量子アルゴリズムでこの問題をはるかに高速に解き、累乗的な高速化を実現できます。 ここで、累乗的であることは、N 回に比べ、約 $\sqrt{$N$}$ 回の評価しか必要でないことを暗に示しています。

アルゴリズムの概要

検索タスクに $N=2^n$ 個の対象項目があり、各項目に $0$ から $N-1$ までの整数を割り当てることで、それらにインデックスを付けたとします。 さらに、$M$ 個の異なる有効な入力があるとします。つまり、$M$ 個の入力があり、$f(x)=1$ であることを意味します。 アルゴリズムのステップは次のようになります。

1. 開始時には、レジスタに $n$ 個の量子ビットがあり、状態 $\ket{0}$ に初期化されています。
2. レジスタ内の各量子ビットに $H$ を適用して、レジスタを一様の重ね合わせになるように準備します。$$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
3. レジスタに次の操作を $N_{\text{optimal }}$ 回適用します。
   1. 解の項目に対して $-1$ の条件付き位相シフトを適用する位相オラクル $O_f$。
   2. レジスタの各量子ビットに $H$ を適用します。
   3. $\ket{0}$ を除くすべての計算の基底状態への条件付きの位相シフト $-1$。 これはユニタリ演算 $-O_0$ によって表すことができます。$O_0$ は、$\ket{0}$ のみへの条件付きの位相シフトを表すためです。
   4. レジスタの各量子ビットに $H$ を適用します。
4. 確率が非常に高い解である項目のインデックスを取得するために、レジスタを測定します。
5. 有効な解であることを確認します。 それ以外の場合は、再度開始します。

$N_\text{optimal}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{{2}\right\rfloor$ は、レジスタを測定することによって正しい項目が取得される確率を最大化する、最適な反復回数です。

注意

ステップ 3.b、3.c および 3.d の合同適用は、文献では通常、グローバーの拡散演算子として知られています。

レジスタに適用される全体的なユニタリ演算は次のとおりです。

$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$

レジスタの状態にステップバイステップで従う

このプロセスを説明するために、2 つの量子ビットだけがあり、有効な要素が $\ket{01} である単純なケースについて、レジスタの状態の数学的変換を考えてみましょう。$

1. 開始時のレジスタは次の状態にあります。$$|\text{register}\rangle=|00\rangle$$

2. 各量子ビットに $H$ を適用した後、レジスタの状態が変換されて次のようになります。$$|\text{register}\rangle=\frac{{1}{\sqrt{{4}}\sum_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$

3. 次に、位相オラクルを適用して以下を取得します。$$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$

4. $H$ が再び各量子ビットに作用して、次のようになります。$$|\text{register}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$

5. ここで、$\ket{00}$ を除くすべての状態に条件付きの位相シフトが適用されます。$$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$

6. 最後に、もう一度 $H$ を適用してグローバーの反復を終了します。次のようになります。$$|\text{register}\rangle=\ket{{01}$$

   上記のステップに従うことにより、1 回の反復で有効な項目が見つかります。 後で説明するように、これは N=4 と 1 つの有効な項目 $N_\text{最適}=な 1$ であるためです。

幾何学的な説明

グローバーのアルゴリズムが動作する理由を確認するために、このアルゴリズムを幾何学的な観点から見てみましょう。 $\ket{\text{bad}}$ が、検索問題の解ではないすべての状態の重ね合わせであるとします。 $M$ 個の有効な解があると仮定すると、次のようになります。

$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

$\ket{\text{good}}$ という状態を、検索問題の解 "である" すべての状態の重ね合わせと定義します。

$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

有効であり、かつ有効でない項目はないので、good と bad は相互に排他的であり、状態 $\ket{\text{good}}$ と $\ket{\text{bad}}$ は直交します。 どちらの状態も、ベクトル空間内の平面の直交を形成します。 この平面を使用してアルゴリズムを視覚化できます。

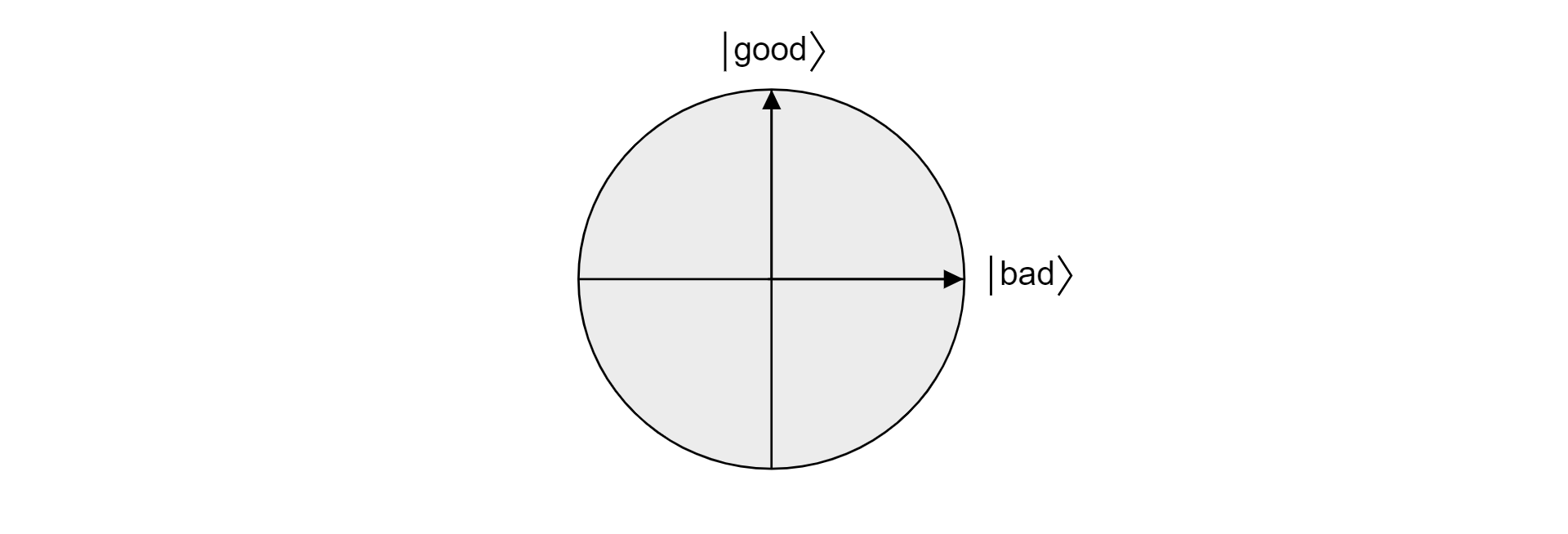
次に、$\ket{\psi}$ が、$\ket{\text{good}}$ と $\ket{\text{bad}}$ にまたがる平面に存在する任意の状態であるとします。 その平面内に存在する任意の状態は、次のように表現できます。

$$\ket{\psi}=\alpha\ket{\text{good}} + \beta\ket{\text{bad}}$$

ここで、$\alpha$ と $\beta$ は実数です。 次に、反射演算子 $R_{\ket{\psi}}$ を加えましょう。ここで、$\ket{\psi}$ は、その平面に存在する任意の量子ビット状態です。 演算子は次のように定義されます。

$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$

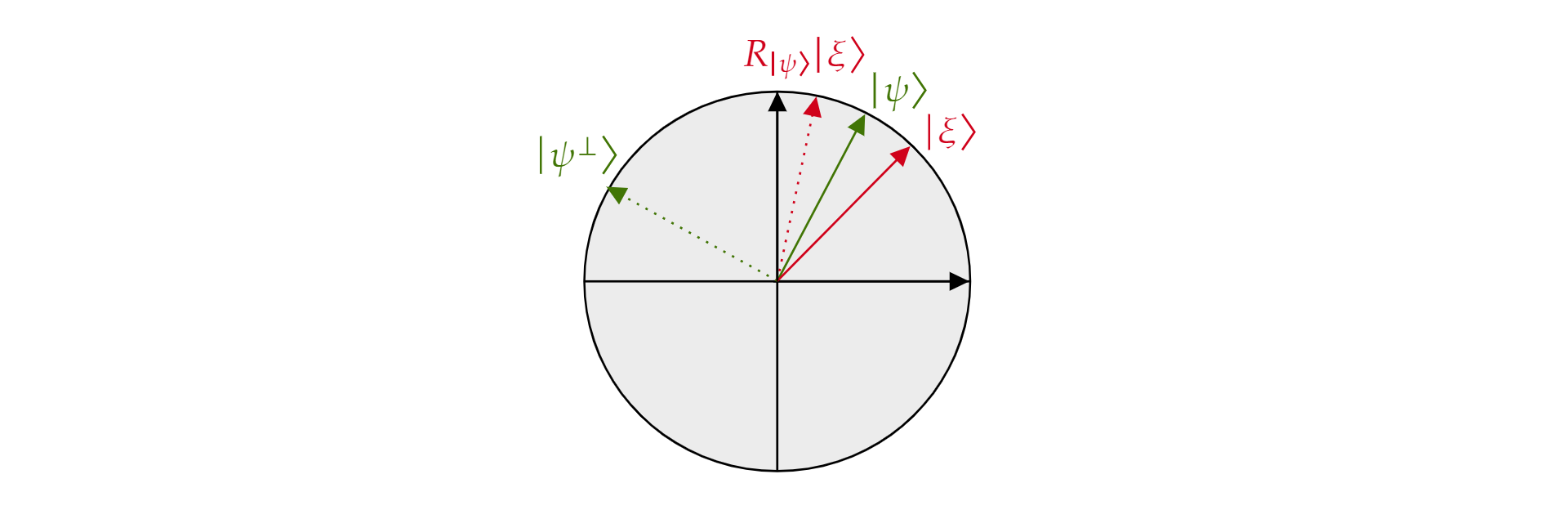
これは $\ket{\psi}$ に関する反射演算子と呼ばれます。それは、$\ket{\psi}$ の方向に関する反射であると幾何学的に解釈できるためです。 これを確認するために、$\ket{\psi}$ によって形成される平面の直交基底と、その直交補空間 $\ket{\psi^{\perp}}$ を考えます。 平面の任意の状態 $\ket{\xi}$ は、このような基底に分解できます。

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

演算子 $R_{\ket{\psi}}$ を $\ket{\xi}$ に適用すると、次のようになります。

$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$

演算子 $R_\ket{\psi}$ により、コンポーネントは $\ket{\psi}$ と直交するように反転されますが、$\ket{\psi}$ コンポーネントは変更されません。 したがって、$R_\ket{\psi}$ は $\ket{\psi}$ に関する反射です。

グローバーのアルゴリズムでは、最初に $H$ をすべての量子ビットに適用した後、すべての状態の一様の重ね合わせから開始します。 これは次のように記述できます。

$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$

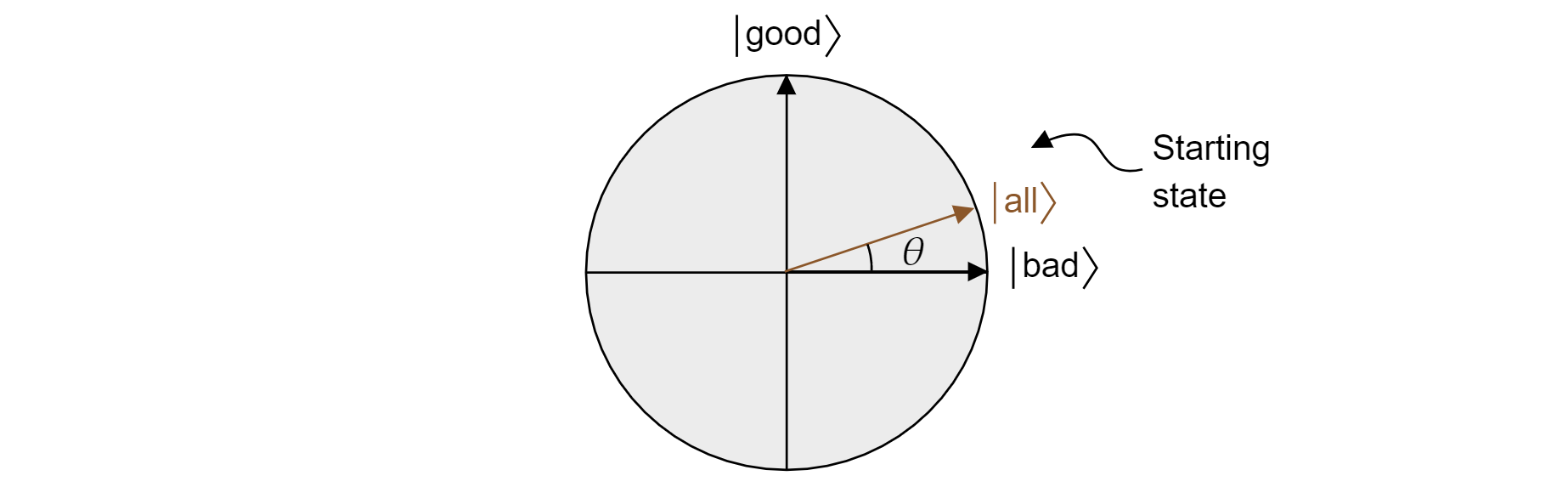
このため、状態は平面内に存在します。 等しい重ね合わせから測定するときに正しい結果を得る確率はすべて^2=M/N$で}}}|$|\braket{\text{}|{\text{、ランダムな推測から期待される値であることに注意してください。

オラクル $O_f$ により、検索問題の任意の解に負の位相が追加されます。 そのため、$\ket{\text{bad}}$ 軸に関する反射として記述できます。

$$O_f = R_{\ket{\text{bad}}}= 2\ket{\text{bad}}\bra{\text{bad}} - \mathcal{I}$$

同様に、条件付きの位相シフト $O_0$ は、状態 $\ket{0}$ に関する反転された反射にすぎません。

$$O_0 = R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I}$$

この事実を知っていれば、グローバーの拡散演算 $-H^{\otimes n} O_0 H^{\otimes n}$ が、状態 $\ket{all}$ に関する反射でもあるかどうかを簡単に確認できます。 次のことを行います。

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{all}} - \mathcal{I}= R_{\ket{\text{all}}}$$

グローバーのアルゴリズムの各反復が、$R_\ket{\text{bad}}$ と $R_\ket{\text{all}}$ という 2 つの反射の合成であることが示されました。

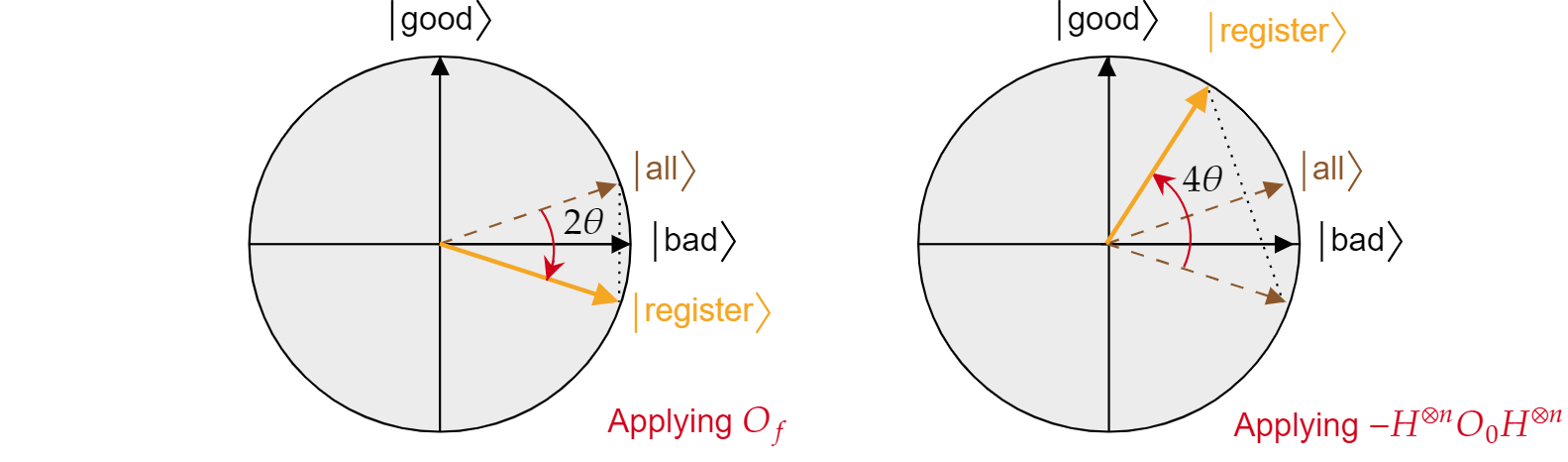
各グローバー反復を組み合わせた効果は、角度 $2\theta$ の反時計回りでの回転です。 さいわい、角度 $\theta$ は簡単に見つかります。 $\theta$ は $\ket{\text{all}}$ と $\ket{\text{bad}}$ の間の角度なので、スカラー積を使用してその角度を見つけることができます。 $\cos{\theta}=\braket{\text{all}|\text{bad}}$ であることがわかっているので、計算する必要があるのは $\braket{\text{all}|\text{bad}}$ です。 $\ket{\text{all}}$ を $\ket{\text{bad}}$ と $\ket{\text{good}}$ について分解することから、次のようになります。

$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$

レジスタの状態と $\ket{\text{良好な}}$ 状態の間の角度は、反復のたびに減少し、有効な結果を測定する確率が高くなります。 この確率を計算するには、適切なレジスタ ^2 を計算$|\braket{\text{するだけで済む$。}}|}|\text{ $\ket{\text{good}}$ と $\ket{\text{register}}$$\gamma (k)$ との間の角度を示すことで (ここで、 $k$ は反復回数)、以下が得られます。

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

したがって、成功の確率は次のようになります。

$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

最適な反復回数

成功の確率を反復回数の関数として書くことができるため、成功の確率関数を (ほぼ) 最大化する最小の正の整数を計算することによって、最適な反復回数 $N_{\text{optimal}}$ が見つかります。

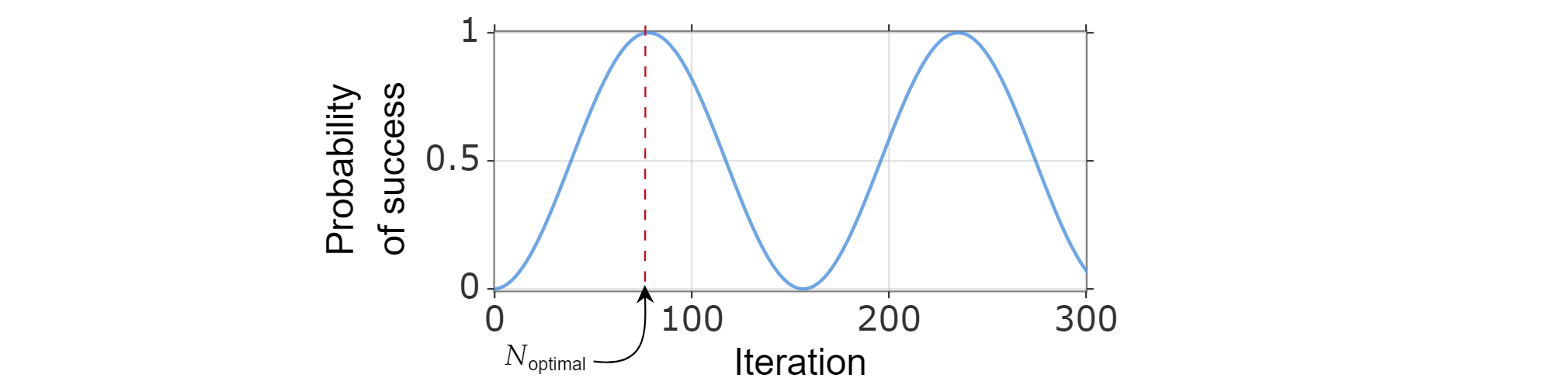
$\sin^2{x}$ が、$x=\frac{\pi}{2}$ で最初の最大値に達することがわかっているので、次のようになります。

$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

次のように表示されます。

$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$

最後のステップでは、$\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$ となります。

したがって、N_最適を選択$して、N_\text{optimal}\left=\lfloor \frac{\pi{4}\sqrt{\frac{}{N}{M}}-\right\frac{{1}{2}\rfloor$ にすることができます。$}$\text{

複雑さの分析

前の分析から、有効な項目を見つけるには、オラクル $O_f$ のクエリが $O\left(\sqrt{\frac{N}{M}}\right)$ 回必要です。 ただし、時間の複雑さに関して効率的にアルゴリズムを実装できるでしょうか。 $O_0$ は、$n$ 個のビットに対するブール演算の計算に基づいており、$O(n)$ 個のゲートを使用して実装可能なことがわかっています。 また、2 層のアダマール ゲート $n$ 個もあります。 したがって、これらのコンポーネントの両方で、1 回の反復あたりに必要なゲートの数は $O(n)$ 個だけです。 $N=2^n$ であるため、$O(n)=O(log(N))$ となります。 したがって、$O\left(\sqrt{\frac{N}{M}}\right)$ 回の反復と、1 回の反復あたり $O(log(N))$ 個のゲートが必要な場合、合計時間の複雑さ (オラクルの実装は考慮しない) は $O\left(\sqrt{\frac{N}{M}}log(N)\right)$ です。

アルゴリズムの全体的な複雑さは、最終的には Oracle $O_f$の実装の複雑さに依存します。 関数の評価が従来のコンピューターよりも量子コンピューターではるかに複雑な場合、技術的にはクエリの使用が少なくても、量子の場合はアルゴリズムの全体的なランタイムが長くなります。

References

グローバーのアルゴリズムについて引き続き学習する場合は、次のいずれかのソースを確認してください。

• Lov K. Grover 氏による元の論文
• Nielsen、M. A の量子検索アルゴリズム のセクション。 &アンプ;Chuang、 I. L. (2010)。 Quantum Computation and Quantum Information (量子コンピューティングと量子の情報)。
• Arxiv.org のグローバーのアルゴリズム

次の手順

• 量子中間表現
• ベクトルと行列
• T ゲートと T ファクトリ
• 複数の量子ビット